基于变换函数的船体曲面参数化修改技术研究＊

胡春平 黄金锋 冯佰威

（武汉理工大学交通学院1） 武汉 430063） （中国舰船研究设计中心2） 武汉 430063）

0 引 言

船体曲面表达是船体设计的一个重点，当进行船体型线优化时，必须要有参数化表达的船体曲面，来自动提供新的船型.目前，对船型参数化自动生成方法主要分为以下两类：一类是基于母型的方法，如融合方法［1－2］，它是基于多个不同母型进行内插值来生成新的船型，通过调整融合参数来实现不同的船型生成，这种方法能在母型光顺的条件下，保证生成的新船型也光顺，很适用于局部变换，但缺点是为了产生尽量复杂的船型，对母型船数量有一定需求；另一类是直接修改控制顶点坐标的方法［3－4］，该方法通过直接操控NURBS控制顶点坐标来改变船体曲面从而产生新的船型，其优点是容易产生各种复杂的船型，但缺点是不能保证变换后船型曲面的光顺性，将该方法应用于船型优化中，由于优化变量非常多，常导致优化无法进行.以上两种方法总体来说是通过对母型的非均匀有理B 样条（non－uniform rational bspline，NURBS）控制顶点的操作来实现新船型的生成；为实现基于计算流体力学（computational fluid hydrodynamics，CFD）的船型自动优化，德国的Stefan Harries等提出了一种全新的船型参数化方法，通过各特征曲线（平底线、平边线等）和相应的剖面曲线函数定义来生成参数化船体曲面，并开发了船型参数化建模的软件Friendship－Framework，但该软件在剖面曲线的定义方面比较难掌握，灵活性太大，对各曲线参数的配合需要建模者自己去协调，这对建模者来说是比较困难的［5］.于雁云在其博士论文中提出了采用变换函数修改船型的方法［6］，其原理是通过构造变换函数，并将该变换函数叠加在母型的船体曲面上，进而求得控制顶点新坐标.该方法可以在很少的参数情况下，进行船型的参数化自动生成，既可避免融合方法中需要建多个母型船而产生手工操作量大的问题，又可克服采用直接修改控制顶点方法导致优化变量多及船体光顺性差的弊端，并且容易实现.本文在此基础之上，分别对局部变换函数和整体变换函数进行了相应的改进，使局部变换函数更合理，整体变换后获得的船体曲面可以更丰富.

1 船体曲面的参数化表达

本文采用NURBS曲面来表达船体曲面，对任一NURBS曲面，可表达为［7］

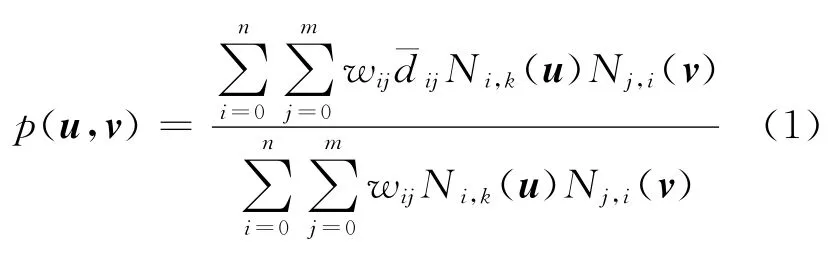
式中：u，v 2个参数是节点向量；m，n 为u，v向控制顶点的个数；dij（0≤i≤j.0≤j≤m）为NURBS控制顶点；wi（i＝0，1，…n）为权重因子，分别与控制顶点dij（i＝0，1，…n）相联系；Ni，k（u）为B样条基函数，它的第1个下标i表示B样条的序号，第2个下标k表示B样条的幂次（等于阶数－1）.其由以下递推公式定义

可知，当固定u，v向的节点矢量时，船体曲面各点的型值由控制顶点的位置决定，因此，通过修改控制顶点的位置可以实现对曲面形状的修改，生成新的船型.

2 变换函数的构造

对一般船型，设初始的母型船体曲面方程表示为

式中：x，y，z为船体曲面上的点.本文的参数化船型变换以母型船体曲面为基础，通过构造坐标变换函数，对母型船体曲面上点的3个方向的坐标进行函数变换来实现新船型的生成.设构造变换后的船型曲面方程如下.

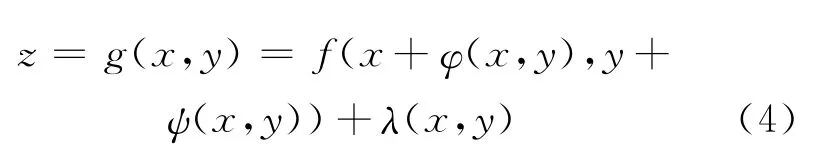
式中：φ（x，y），ψ（x，y），λ（x，y）分 别为X，Y，Z 轴方向上的坐标变换函数.则可知，当φ（x，y）＝ψ（x，y）＝λ（x，y）＝0时，变换后得到的船型就是母型船的船型；当这3个函数有任何1个不为零时，就可以产生和母型不同的船型.虽然通过变换函数可以产生和母型不同的新船型，但这并不能保证船型的光顺性.因此，需要对变换函数及其参数取值做相应的限定.

具体实行船体曲面变换时，由于文中的曲面是NURBS参数化的曲面，因此只需修改控制顶点，然后由NURBS原理可自动反映到船体曲面的型值点上去，从而实现了船体曲面的变换.这里对船型的变换分为两类考虑：对船型的局部线型进行变换；对全船的线型进行变换.

对船型曲面进行局部变换，可以选择下面的变换函数

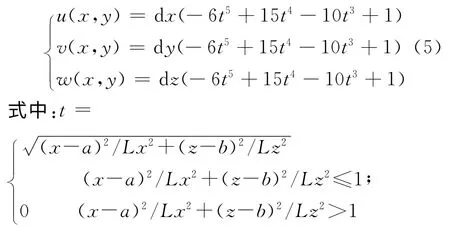
dx，dy，dz，a，b，Lx，Lz，为可变参数，x，z 为控制曲面控制顶点，利用该函数对船型曲面进行修改的局部变换区域为XOZ 平面上以点（a，b）为中心、Lx 和Lz 为长、短轴的椭圆形区域.进行船型变换时，只对椭圆区域内的控制顶点进行坐标变换.根据式（5）可知，参数t的值域为［0，1］；又函数f（t）＝－6t5＋15t4－10t3＋1在0≤t≤1上为单调递减函数，取值也为［0，1］，且在t＝0时，坐标值变化最大，但变化率为0；在t＝1处，坐标值变化最小（不变化），变化率也为0，且在变量域内，其取值成渐进变化的，该函数特性见图1.

对船体曲面进行整体变换，选择下面的坐标变换函数

式中：dxf，dxa分别为X 轴方向舯前段和舯后段变换的参数；dy，dz 分别为沿船宽方向和型深方向的变化参数；ep 亦为型深方向变化参数；Lmax，Bmax，D 分别为最大船长、最大船宽和型深.

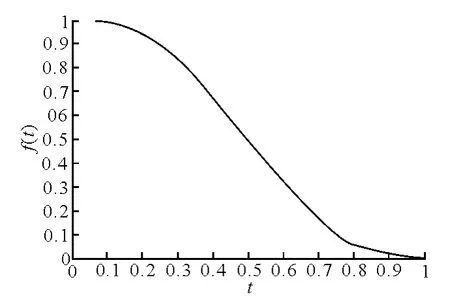
图1 函数特性图

3 船型曲面的光顺条件

文献［6］在数学上给出了曲面光顺性准则，即任何曲面函数只要满足下面3个条件就能够保证曲面光顺.

1）坐标变换函数需要满足C2（2 阶导数）连续性方程

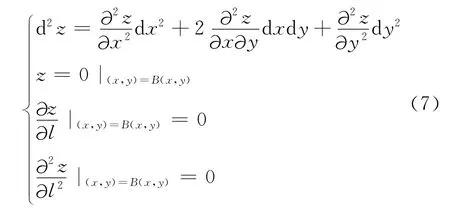
式中：B（x，y）＝0 为一封闭曲线，曲线内部区域为φ（x，y），ψ（x，y），λ（x，y）的作用域，即在B（x，y）＝0区域外，φ（x，y）＝ψ（x，y）＝λ（x，y）＝0，也就不受影响.

2）坐标变换函数不会使变换后的船体曲面产生多余的拐点.

3）坐标变换函数在作用域内曲率变化是均匀的.

要保证经船型变换函数进行船型变换后的新船体曲面仍然是光顺曲面，即要证明z＝g（x，y）＝f（x＋φ（x，y），y＋ψ（x，y））＋λ（x，y）是光顺的船型曲面，则应证明变换后的船型满足上文中提到的曲面光顺的3个条件.研究表明，只要选择合适、满足连续光顺条件的坐标函数，并且设定合适的变换范围则可以保证船体曲面的光顺性，由光顺条件易知本文中选择的变换函数（公式5、6）满足这几个条件，即可以保证变换后船型曲面的光顺性，详细的光顺性证明参考文献［6］.

4 船型变换示例及其CFD 计算

4.1 局部变换实例

利用已给出的局部变换函数式（4），对1300 TEU 集装箱船球鼻首部位进行局部变换，变换前后的线型对比如图2～4所示.其中图2为变换前的船体首部，图3～4为变换后的球鼻首部位，图3船型变换采用的相关参数选择为：a＝0，b＝6.7086，dx＝2，dy＝0，dz＝2.5，Lx＝4，Lz＝3；图4船型变换采用的相关的参数选择为：a＝9.2653，b＝6.2178，dx＝－2，dy＝0，dz＝－1.4，Lx＝4，Lz＝3.

图2 变换前的母型

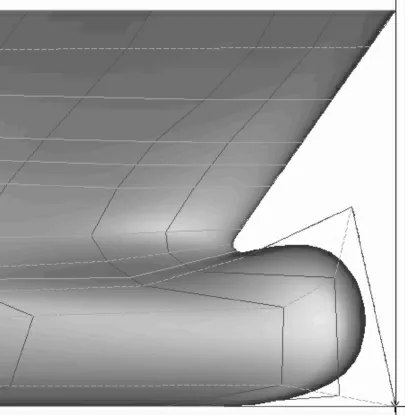
图3 变换后的船型

图4 变换后的船型

4.2 整体变换实例及CFD计算

在整体变换中，以戴维泰勒水池DTMB5415标模作为初始船型，采用整体变换（见式（5））进行线型变换，变换前后的型线对比见图5～6.采用的相关参数为：dxf＝－0.0141，dxa＝－0.238，dy＝－0.0347，dz＝0.329，ep＝－0.261.

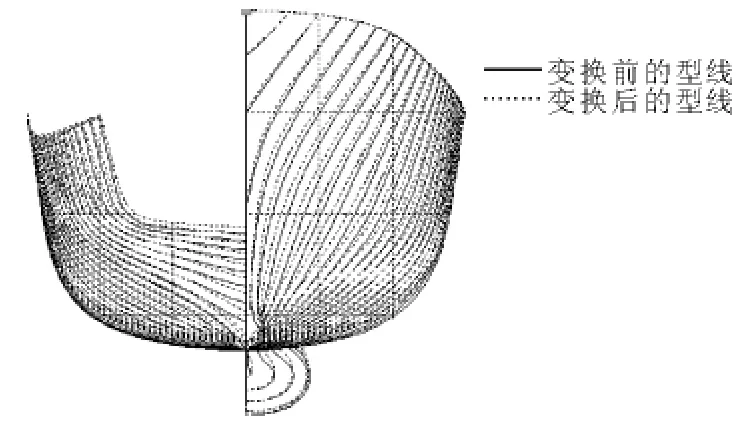
图5 DTMB5415线型整体变换前后横剖线对比

图6 DTMB5415线型整体变换前后纵剖线对比

以上2种变换方法的参数是在其值域范围内随机选取.

对变换前后的线型应用CFD 技术进行船体兴波阻力数值模拟，计算结果见图7.可以看到，船型变换前后船体周围相应的流场和压力场发生了改变.图8所示的为船型变换前后的纵向波切图对比，变换后船体的波高有了明显的变化.图9～10为变换前后的船体表面压力分布图，可以看到船体表面的压力场分布发生了较大的改变.

图7 船型变换前后的波形对比

图8 变换前后的纵向波切图对比（y／L＝－0.0728）

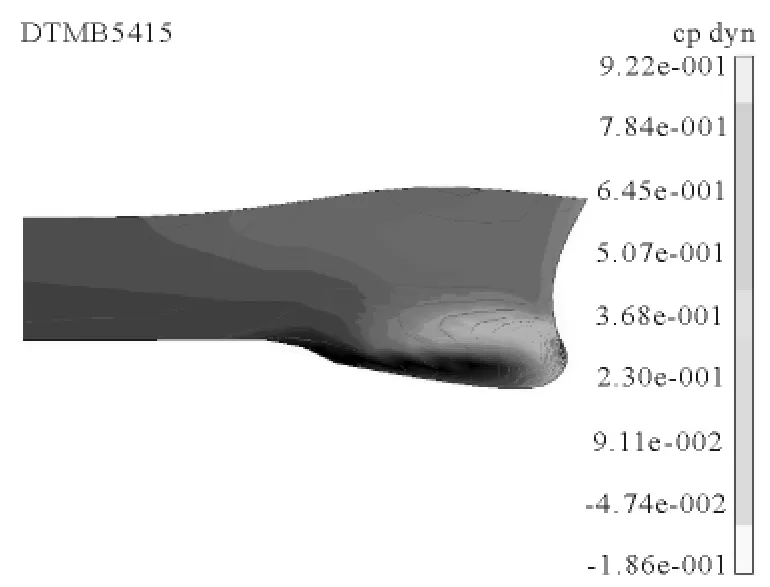
图9 母型船船体表面压力分布

图10 变换后船体表面压力分布

5 结束语

实现船体型线自动优化的关键是能够使用较少的参数控制船型的自动生成，并保证曲面的光顺性.本文采用了基于变换函数修改船型曲面的方法，该方法仅仅需要很少的几个参数就可实现船体曲面局部和整体变换，并保证了船型曲面的光顺性.尽管该方法未用到船型优化中，但却为后期基于CFD的船型精细优化研究打下了很好的基础［8］.

［1］YUSUKE T，SATOSHI T，TOKIHIRO K.CFDbased multi－objective optimization method for ship design［J］.Int.J.Numer.Meth.Fluids，2006，52：499－527.

［2］冯佰威，刘祖源，詹成胜，等.基于船型修改融合方法的参数化建模技术［J］.计算机辅助工程，2010，19（4）：3－7.

［3］HYUNYUL K.Multi－objective optimization for ship hull form design［D］.George：George Mason University，2009.

［4］刘祖源，冯佰威，詹成胜.船体型线多学科优化［M］.北京：国防工业出版社，2010.

［5］ABT C，BADE S D，HARRIES B S.Parametric hull form design－a step towards one week ship design［C］.8th International Symposium on Practical Design of Ships and Other Floating Structures，PRADS 2001，Shanghai，September 2001.

［6］于雁云.船舶与海洋平台三维参数化总体设计方法研究［D］.大连：大连理工大学，2009.

［7］张 萍，朱德祥，何术龙.参数化的船型设计方法［J］.中国造船，2008，49（4）：26－35.

［8］冯佰威，刘祖源，詹成胜，等.船舶CAD／CFD 一体化设计过程集成技术研究［J］.武汉理工大学学报：交通科学与工程版，2010，34（4）：649－651.