物流中心选址与规模的层次优化模型＊

王建忠 杜 纲

（中国民航大学空中交通管理学院1） 天津 300300） （天津大学管理学院2） 天津 300072）

0 引 言

目前，物流中心选址问题的定量方法主要包括重心法、Cluster法、Baumol－Wolfe法、混合0－1整数规划法、模拟法.重心法将物流系统中的需求量点和资源点看成是分布在某一平面范围内的物流系统，各点的需求量和资源量分别看成是物体的重量，物流系统的重心作为物流网点的最佳设置点.Cluster法的基本思想是先将物流中心定位在各个需求点，然后通过对需求点进行组合以降低物流中心的数目，并根据组合后的需求点的几何重心安排新的物流中心地址，直到总费用不再降低为止.Baumol－Wolfe法［1］是一个整数规划方法，在满足供应及需求约束条件下，追求由运输费、发送费及可变费用组成的总费用最低，以此选定物流中心，这种模型计算简单，只要运用一般运输规划的计算方法即可，避免了混合整数规划模型的求解困难.混合0－1整数规划模型［2］是选址问题最常用的模型，Holmberg［3］研究了非线性运输成本和非受限容量条件下的选址问题；Barahona和Jensen［4］在混合0－1整数规划模型中不仅考虑了固定成本和运输成本，并且考虑了库存成本；Klose和Drexl［5］综述对选址问题的定量方法进行了详尽的综述.以上方法都是单层优化方法，未能考虑供应链上下游企业在进行优化决策时内在的相互影响.

为克服单层优化方法的这一缺点，不少学者应用双层规划来描述物流中心的选址问题.孙会君等［6］对选址问题进行了详细的研究.管小俊等［7］在下层规划中考虑了新建物流中心与原物流中心的竞争问题.Taniguchi［8］建立了公共物流终端选址的双层规划模型，并设计了遗传算法进行求解；Sun等［9］建立双层规划模型，上层考虑满足需求的广义成本（非线性）和建立物流中心的固定成本，下层考虑消费者对物流中心的选择.本文综合考虑了进货时分销商对物流中心的选择和生产商内部生产物流之间的相互影响，建立了基于层次优化的物流中心选址与规模模型，并针对模型特点提出基于遗传算法的求解方法，最后用算例验证该方法的有效性.

1 问题描述

某生产企业在各地共设有N 个分厂生产一种产品.该企业共有M 个需求地，考虑在这些需求地中选择若干个建立大型物流中心，而没有被选为物流中心的需求地由分销商满足需求，分销商从物流中心进货.生产商需确定：（1）选择哪些需求地建立物流中心，将物流中心建成何等规模；（2）各物流中心由哪些分厂供货，如何安排运输流.分销商需确定：为满足各地需求，需从哪些物流中心进货，进货多少.二者的决策相互影响、相互制约，生产商拥有更大的决策权力，选择物流中心地址和规模，间接影响分销商的运输成本；分销商通过调整进货量在各物流中心的分配可以影响生产商的选址及规模决策.

为方便建立数学模型，使模型不至于太复杂而又有一定的实用性，做如下模型假设：（1）生产商为上层决策者，处于决策的主导地位；分销商为下层决策者处于决策的追随地位；（2）从物流中心到需求地的运输费用由分销商承担，两地间的单位运输费用为常量，与运输量无关；（3）被选为物流中心的需求地由工厂直接供货，没有被选为物流中心的需求地由同一家分销商代理；（4）不考虑与其他制造厂商间的竞争；（5）各地需求较长时期内相对稳定.

2 模型的建立

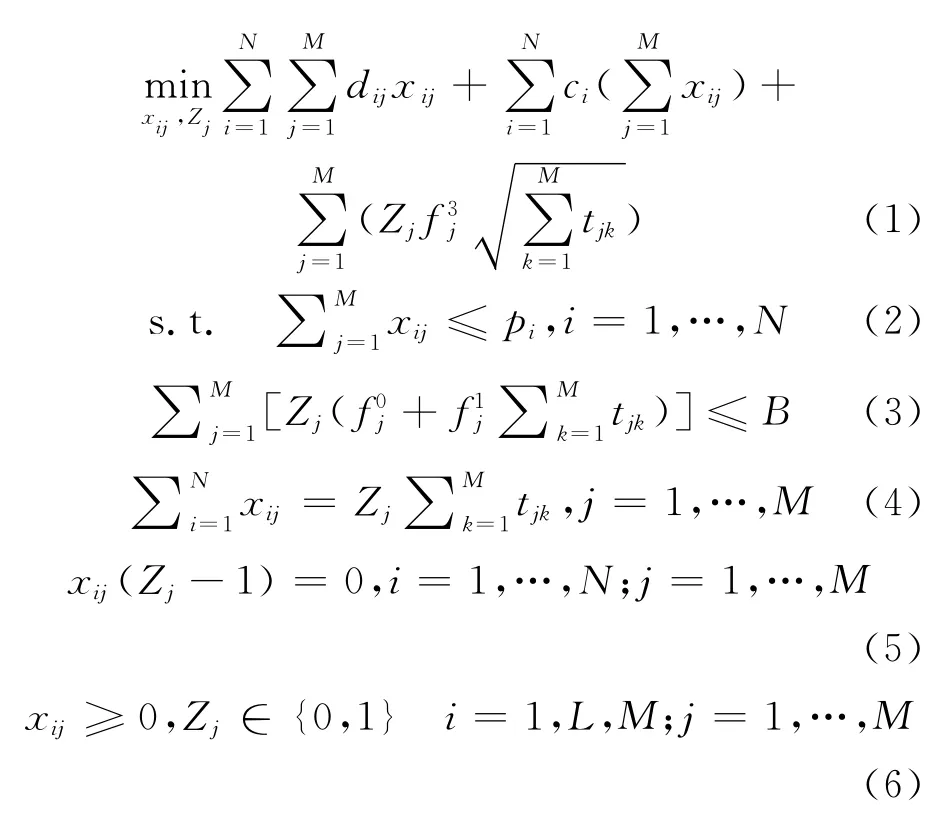
其中：tjk是下面规划的解：

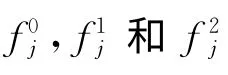
式（1）～（6）为上层规划，决策者为生产商.上层目标函数：（1）为生产商的生产成本、运输成本及物流中心运营费用最小；约束条件（2）为各物流中心从工厂i进货的总量不应超过工厂的最大生产能力；（3）为建立物流中心的总费用不应超过预算；（4）为平衡约束，物流中心的进货量应等于输出量；（5）使工厂只向被选为物流中心的需求地运输产品；（6）为上层决策变量xij的非负约束和Zj的0－1约束.

式（7）～（11）为下层规划，决策者为分销商.下层目标函数（7）为分销商从物流中心进货的平均运输费用最低；（8）为各地需求都必须满足；（9）使各需求地均从被选为物流中心的需求地进货；（10）为物流中心的规模应介于最大和最小规模之间；（11）为下层决策变量tjk的非负约束.

3 模型求解

双层优化模型（1）～（11）是混合整数双层规划，通过分析发现模型具有以下特点：（1）上层变量Zj是0－1变量，由于选址模型中的备选数目一般比少，故Zj的组合数目相对较少；（2）上层决策变量中只有Zj对下层决策有影响.而xij只是在下层变量tjk确定以后，对上层目标函数有影响.上下层的决策顺序为：上层给出Zj，下层根据Zj确定tjk返回上层，最后上层确定xij；（3）下层的目标函数为分式，分式规划不是凸规划，不易找到全局最优解.

针对模型特点（1）拟对上层规划采用隐枚举法，用投资预算约束和规模约束除去不可行的Zj取值.

针对模型特点（2），可以将上层决策中的生产运输问题分解出来单独求解.模型如下.

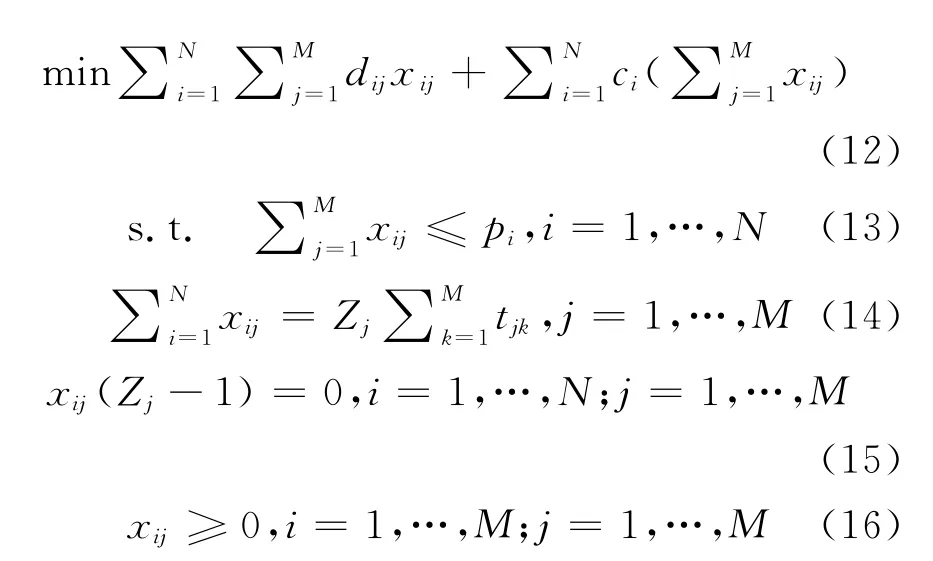
针对模型特点（3）拟采用遗传算法对下层规划进行求解.

算法基本思想：基于对模型的特点分析，可采用直接搜索法对模型进行求解.上层不断生成Zj的组合，将其作为参数代入下层，利用遗传算法求解下层规划得到下层满意解tjk.将Zj和tjk代入生产运输模型，求出xij.将xij代入上层规划用上层约束检验解｛Zj，tjk，xij｝是否可行，若可行，记录上层目标函数的值.最后比较所有可行组合下的目标值确定最优解.算法具体步骤如图1所示.

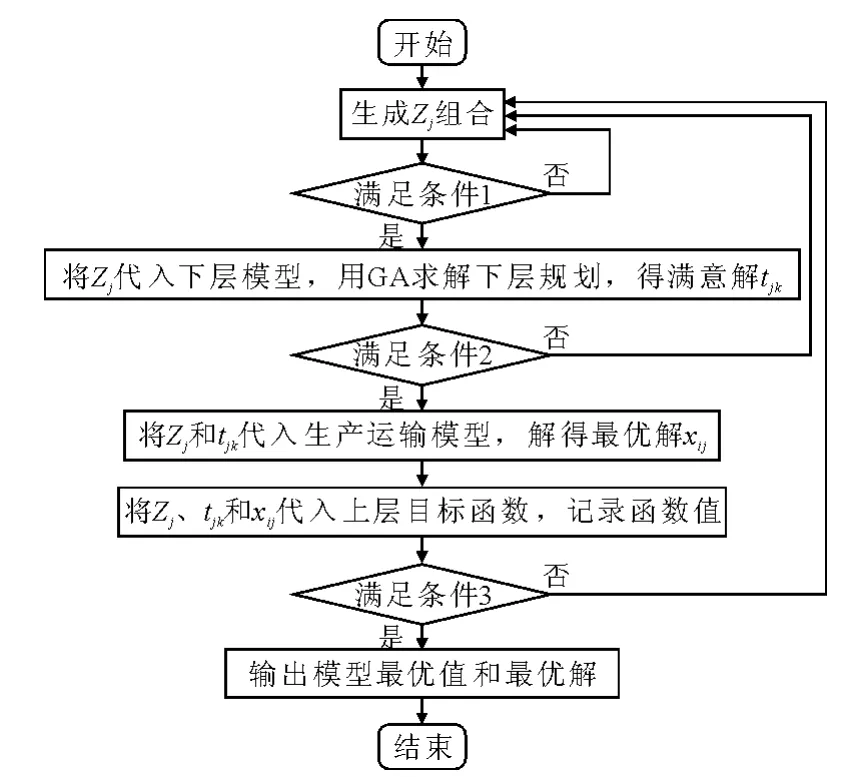
图1 算法步骤

4 算 例

某天然气生产商PCCL拥有2座天然气生产厂F1和F2，与天然气分销商XA 合作满足A1，A2，A3，A4，A5，A6，A7，A88个城市的需求，计划在合适的需求地建立合适规模的天然气物流中心，资金预算B＝2750万元，使其总成本（生产成本、工厂到物流中心的运输成本、物流中心经营成本）最小.具体数据如表1～表4所列.

表1 工厂生产数据

表2 工厂到各需求地的单位运输成本 元／m3

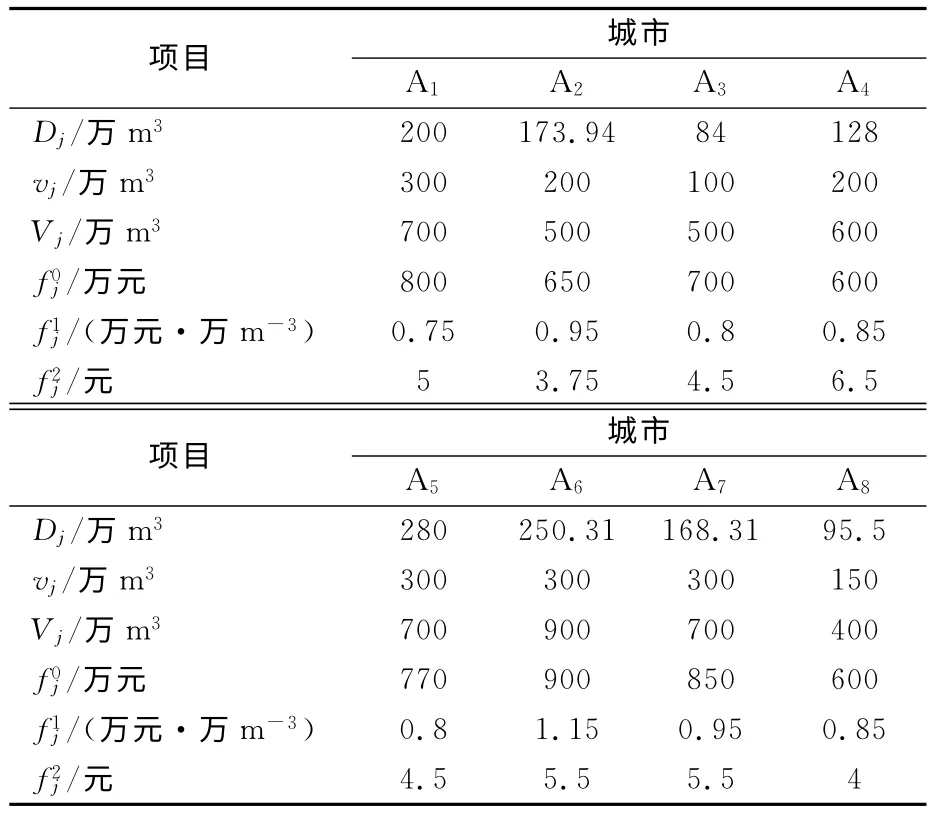
表3 需求地信息

表4 需求地间单位运输成本 元／m3

应用上一节提出的算法求解，其中遗传算法采用实数编码方案、转盘赌选择法和精英保留法结合的选择策略、线性交叉策略，种群个体数目为20，交叉概率取0.6，变异概率取0.03，最大迭代次数为200.用Matlab 6.5编程解得Z1＝Z5＝1，即在需求地A1和A5建立物流中心，x11＝900，x25＝980，即生产商从工厂F1，F2分别运往A1，A5天然气为900万和980万m3，同时也是2个物流中心的规模大小；生产商的最低总经营成本为2617.34万元，分销商的最低平均单位运输成本为0.6675元／m3.分销商的运输策略如表5所列.

表5 计算结果 万m3

使用遗传算法对下层规划求解，迭代次数超过90后，最优值即保持稳定.当Z1＝Z5＝1时，下层规划的遗传算法收敛情况如图2所示.

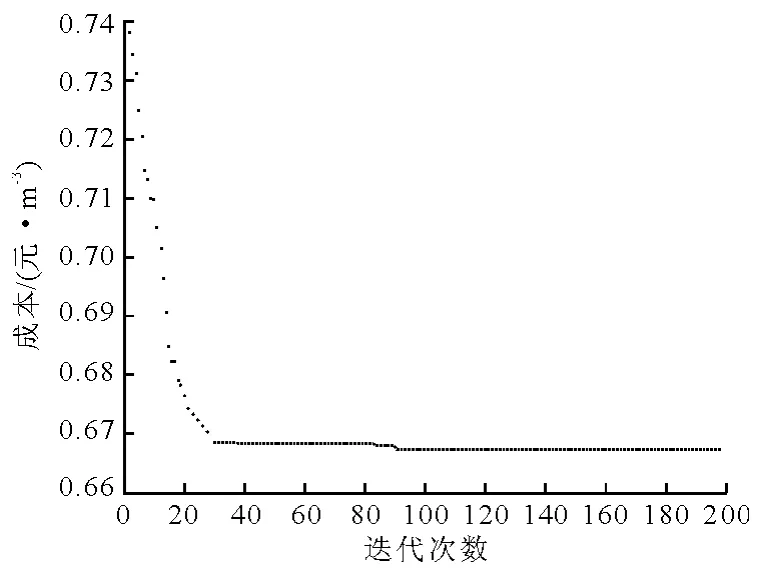
图2 Z1＝Z5＝1时下层算法收敛情况

5 结束语

本文建立了基于层次优化的物流中心选址与规模模型，充分考虑了决策过程中生产商与分销商相互影响的关系，根据模型的具体特点提出了基于遗传算法的求解方法，最后用算例验证了模型和方法的有效性.

［1］BAUMOL W J，WOLFE P.A warehouse－location problem［J］.Operations Research，1958，6（2）：252－263.

［2］BROWN G G，GRAVES G W，HONCZARENKO M D.Design and operation of a multi commodity production／distribution system using primal goal decomposition［J］.Management Science，1987，33（11）：1469－1479.

［3］HOLMBERG K.Exact solution methods for uncapacitated location problem with convex transportation costs［J］.European，Journal Operational Research，1999（114）：127－140.

［4］BARAHONA F，JENSEN D.Plant location with minimum inventory［J］.Mathematical Programming，1998（83）：101－111.

［5］KLOSE A，DREXL A.Facility location models for distribution system design［J］.European，Journal Operational Research，2005（162）：4－29.

［6］孙会君，高自友.考虑路线安排的物流配送中心选址双层规划模型及求解算法［J］.中国公路学报，2003，16（2）：115－119.

［7］管小俊，王喜富，王翠华，等.基于竞争的物流中心选址双层规划模型及算法研究［J］.武汉理工大学学报：交通科学与工程版，2009，33（5）：956－959.

［8］TANIGUCHI E.Optimal size and location planning of public logistics terminals［R］.Transport.Res.1999（35E）：207－222.

［9］SUN Huijun，GAO Ziyou，WANG Jianjun.A bilevel programming model and solution algorithm for the location of logistics distribution centers［J］.Applied Mathematical Modeling，2008（32）：610－616.