基于磁流变阻尼器的车辆悬架振动优化控制*
赵 强 米 磊 尹佳星
(东北林业大学交通学院 哈尔滨 150040)
0 引 言
近年来磁流变(MR)阻尼器作为智能型减振器,在车辆悬架振动的半主动控制领域中日益得到重视.文献[1]研究了配备MR 阻尼器的1/4车悬架振动的神经网络半主动控制,文献[2]根据MR 阻尼器的Bouc-Wen模型研究了1/4车悬架振动的开关控制.然而,由于MR 阻尼器所固有的高度非线性特性,当MR 阻尼器用于振动控制时,需要解决如何由控制规律所决定的控制力得到其输入电压的逆向问题.目前,通常的解决方案是根据开关控制律来调整输入电压[3]以及开关最优控制算法[4].由于MR 阻尼器的输入电压只能在最小值和最大值之间切换,这样就没有实现控制信号的连续可调,必然会限制MR 阻尼器的性能.
鉴于神经网络可以逼近任意的非线性函数,本文提出运用神经网络技术建立非线性控制装置MR 阻尼器的神经网络模型来模拟其逆向动特性,同时与LQR 主动控制方法结合形成闭环回路对车辆悬架系统进行半主动控制研究.运用该方法能够通过逆模式神经网络得到连续的控制电压,从而实现阻尼力的连续可调,充分发挥MR阻尼器的智能特性,从而实现控制车辆悬架系统振动响应的目的.
1 MR 阻尼器神经网络逆模式控制的分析方法
1.1 控制策略
图1为车辆悬架系统在路面激励的作用下进行MR 阻尼器神经网络逆控制的整体框图.控制器根据车辆悬架系统的振动响应计算出期望的控制力,期望控制力连同阻尼器位移一起进入到MR 阻尼器的神经网络模型,它的输出就是在当时悬架系统的振动响应下,为了使MR 阻尼器产生与期望控制力相对应的控制电压,该电压输入给MR 阻尼器使之产生接近期望控制力的输出力作用到车辆悬架系统,从而降低其振动响应.
1.2 MR 阻尼器半主动约束
本文采用Spencer 等提出的修正的Bouc-Wen模型来描述MR 阻尼器的力学特性,该模型引入2个内变量,构造了包含14个待定参数的微分方程模型[5].
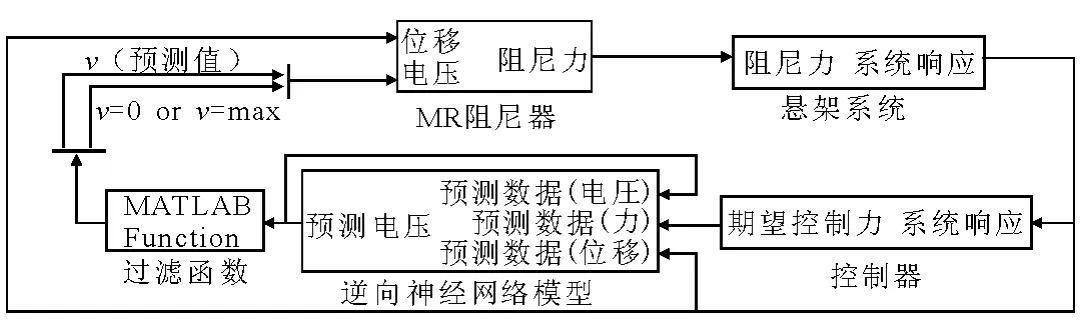
图1 控制策略框图
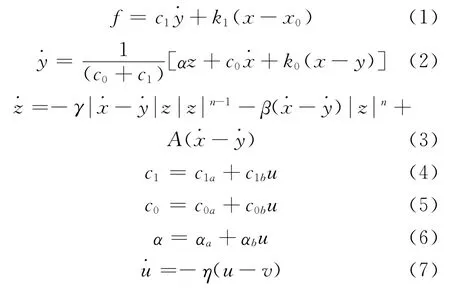
式中:x 和f 分别为MR 阻尼器的位移和阻尼力;c1a,c0a,αa为无电压时的系数;c1b,c0b,αb为随电压变化的系数;u为联系f 和v 的中间变量;v 为阻尼器的驱动电压;γ,β,A 为迟滞特性相关系数;n为指数系数,一般取2.式(1)~(7)描述的MR 阻尼器力与位移以及力与速度的关系曲线见图2.
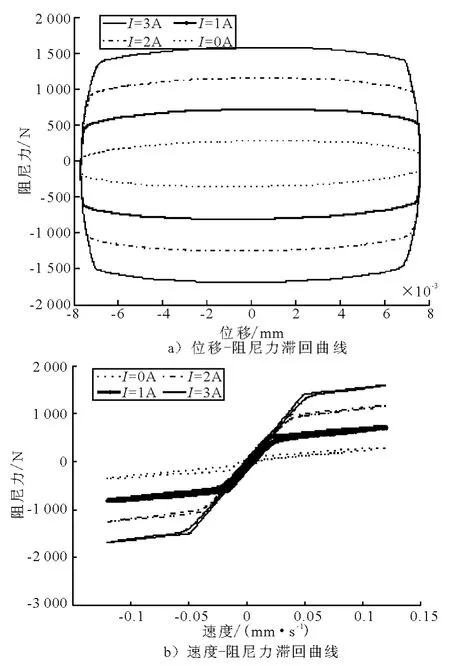
图2 MR 阻尼器位移-阻尼力、速度-阻尼力滞回曲线
从图2b)可看出,MR 阻尼器所能提供的阻尼力位于阻尼力-活塞速度平面的第I,III象限,而不能如主动控制元件那样提供4个象限的力,也就是说只有当期望控制力与活塞速度两者符号相同时,磁流变阻尼器才能输出跟踪期望控制力的阻尼力,可描述为



1.3 MR 阻尼器的逆向神经网络模型
MR 阻尼器逆向神经网络预测实质上是由下列方程所示的输入输出之间的非线性映射.
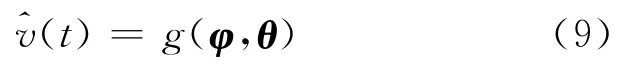

其中:nv,nx和nf分别是输入电压、位移和阻尼力的时间步长数.图3为其训练框图.
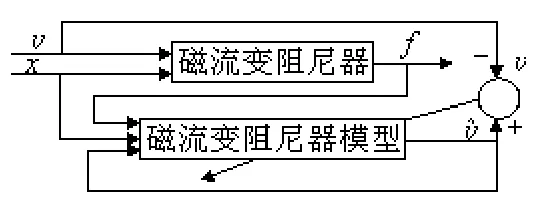
图3 MR 阻尼器的逆向神经网络模型训练框图
由Kolmogorov逼近定理可知,具有单隐层的(修改)BP神经网络可以逼近任意具有有限间断点的非线性函数,因此本文选用一个3 层BP神经网络来描述MR 阻尼器的逆向动特性.网络的输入层有9个节点,由3个连续时间步长的输入电压、位移和阻尼力组成(nv=nx=nf=3);隐层有20个节点,输出层有1个节点,是当前时刻的控制电压.此外,隐层和输出层的传递函数分别采用tansig函数和purelin函数,以目标输出和网络输出的均方误差为网络性能函数,网络训练函数采用标准梯度下降算法traingd函数(修改).训练和验证数据选取如下位移和输入电压由Gaussian白噪声生成,频率范围分别是0~3 Hz和0~4Hz,阻尼力由式(1)~(7)求得.以500Hz采样频率对上述生成数据采样20s,共产生10000个数据对用来对该逆模型进行训练和验证,在使用中,采样数据要进行规则化处理(均值为零方差为1).图4所示为控制电压目标值和预测值的比较,从图中可看出,预测值能够很好的跟踪目标值,说明网络训练比较成功,具有很强的泛化能力.
1.4 车辆悬架动力学模型
为了简化控制模型,突出研究问题的主要方面,图1中的车辆悬架系统采用简化的1/4车二自由度悬架系统模型,见图5.

图5 1/4车二自由度车辆悬架系统模型
由图5得悬架系统的动力学方程

式中:m1为半主动悬架非簧载质量,kg;m2为半主动悬架簧载质量,kg;k1为轮胎径向刚度系数,N/m;k2为悬架刚度系数,N/m;c为磁流变阻尼器的无场阻尼系数,N·s/m;z2为车身簧载质量的垂直位移,m;z1为车身非簧载质量的垂直位移,m;z0为路面激励,m;fd为磁流变阻尼器的有场阻尼力,N.
2 最优控制器的设计
将训练完成的MR 阻尼器神经网络逆向模型用于实现控制算法所解算出的控制力的要求,为了尽可能的降低车身垂直加速度 悬架动挠度及轮胎动载荷使车辆获得较高的行驶平顺性和操纵稳定性,同时不消耗太多能量,本文综合考虑悬架各种性能指标,采用LQR 算法[6]进行控制器的设计.
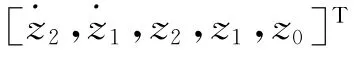
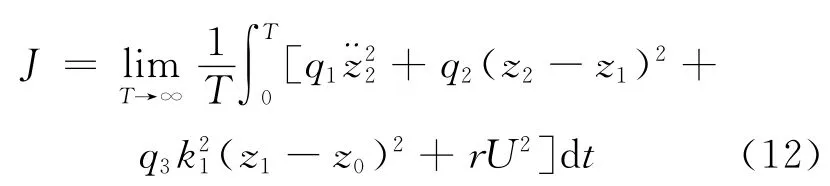
式中:q1,q2,q3为加权矩阵q系数,决定着悬架系统的性能;r为约束系数.加权系数可以书写为矩阵形式
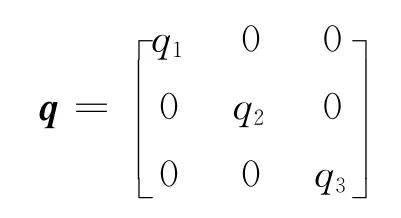
则性能指标公式转换为

按照矩阵的运算规律,将上式展开可得

设Q=CTqC,N=CTqD,R=r+DTqD,则式(14)可写为
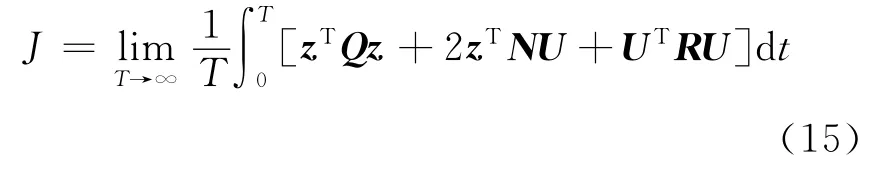
确定车辆参数和加权系数之后,运用黎卡提方程求出反馈增益矩阵K.

求出增益矩阵K 之后,最优控制器的设计基本完成.根据任意时刻的反馈状态变量 z(t) ,就能得出t时刻作动器的最优控制力 U(t) :
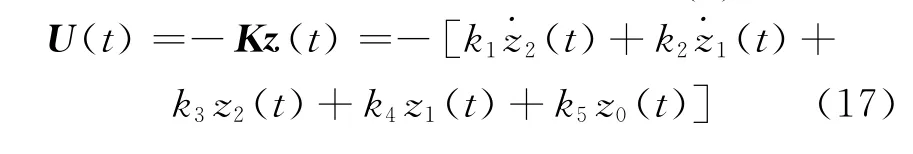
3 仿真分析
3.1 减振效果分析

为更好地分析本文提出的MR 阻尼器神经网络逆控制的减振效果,将其与被动悬架作比较.图6为悬架加速度 动挠度以及轮胎动载荷的仿真结果,由图可知,基于神经网络逆控制的悬架系统相比于被动悬架性能有明显的改善,表1为其相应的均方根值.由表1 可知,基于MR 阻尼器神经网络逆模型控制的半主动悬架加速度较被动悬架下降20.72%,动挠度下降了22.11%,轮胎动载荷下降了10.67%,有效降低了车身振动对人体的影响,显著提高了车辆悬架系统的动态舒适性.

图6 仿真结果
3.2 频域减振分析
随机路面激励下的车辆悬架加速度功率谱密度低频放大(20 Hz)图见图7.从中可以看出,神经网络逆模型控制作用下的车辆悬架加速度在高频处因变频干扰基本和被动悬架相同,但在车身共振(1~1.5 Hz)和人体垂向最敏感(4~12.5 Hz)[8]这2个低频范围内,神经网络逆模型控制有效地降低了车辆悬架加速度.在1~1.5 Hz区间,神经网络逆模型控制较被动控制加速度改善不少,而在4~8Hz这个人体内脏器官最易产生共振的频率范围内,神经网络逆模型控制较被动控制加速度也有显著降低,进而减轻乘员乘坐的不舒适性.
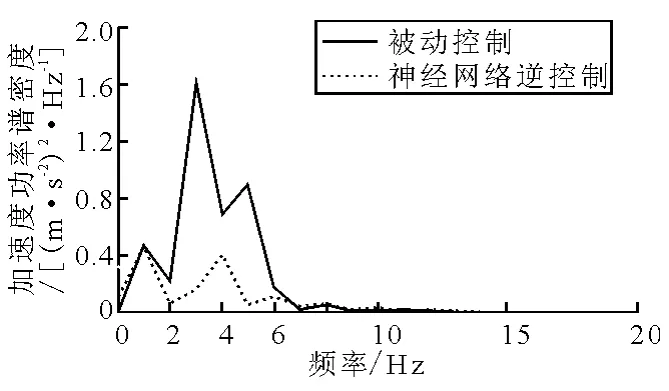
图7 加速度功率谱密度低频放大图
图8所示为MR 阻尼器的输入控制电压以及由此产生的阻尼力,为了比较还给出了LQR主动控制的期望控制力,从图中可见,MR阻尼器实际出力跟随期望控制力较为接近.

图8 MR 阻尼器的输入电压及输出阻尼力
4 结 论
1)针对MR 阻尼器的高度非线性特性,运用神经网络模型来模拟MR 阻尼器的逆向动特性,该神经网络模型直接提供了为产生由最优控制算法计算出的期望控制力所需连续输入电压的估计手段.
2)时域和频域内的数值仿真结果表明:在控制策略中通过引入MR 阻尼器的逆向神经网络模型,可有效的改善车辆悬架系统的性能,同时使MR 阻尼器的连续调节主动控制成为可能,为进一步的工程应用奠定了理论基础.
[1]GUO D L,HU H Y,YI J Q.Neutral network control for semi-active vehicle suspension with a Magnetorheological Damper[J].Journal of Vibration and Control,2004,10(3):461-471.
[2]YAO G Z,YAP F F,CHEN G,et al.MR damper and its application for semi-active control of vehicle suspension system[J].Mechatronics,2002 (12):963-973.
[3]DYKE S J,SPENCER B F.A comparison of semiactive control strategies for the MR damper[J].Intelligent Information Systems,1997(8-10):580-584.
[4]DYKE S J,SPENCER B F,SAIN M K.Modeling and control of magneto-rheological dampers for seismic response reduction[J].Journal of Smart Materials and Structures,1996(5):565-575.
[5]SPENCER B F,DYKE S J,SAIN M K,et al.Phenomenon logical model of a magneto-rheological damper[J].ASCE Journal of Engineering Mechanics,1996(3):1-23.
[6]赵 亮,文桂林.基于磁流变阻尼器的车辆半主动悬架最优控制的研究[J].汽车工程,2008,30(4):341-343.
[7]俞 凡,林 逸.汽车系统动力学[M].北京:机械工业出版社,2005.
[8]DAVE C,喻 凡.车辆动力学及其控制[M].北京:人民出版社,2004.

