径向多圈层桩-土耦合振动模型研究

薛国强，张 琳，周 燕

（1.常熟理工学院 管理学院，江苏 常熟 215500；2.常熟中法水务有限公司，江苏 常熟 215500；3.常熟市住房和城乡建设局，江苏 常熟 215500）

桩基振动理论是桩基抗震、防震设计以及各种动力测试方法的理论依据.近年来国内外对桩的振动研究取得了丰硕的成果，其进展主要表现在对桩土相互作用问题的处理上.从早期相对简单的Voigt体模型[1-3]和平面应变模型[4-6]到胡昌斌等[7]提出的考虑桩周土竖向波动模型，再到王奎华等[8]提出的同时考虑土体径向和竖向位移的真三维土体波动模型，这些工作有力地促进了桩基振动理论的发展，但这些研究工作还都是把桩周土体视为均质或纵向分层均质线性弹性材料.而在桩的施工过程中，由于挤土、松弛效应及其他因素的影响，在距离桩中心不同范围内，土的性质、参数会发生不同程度的改变，也就是说在桩的直径方向，土体性质也会存在不均匀性，周铁桥、杨冬英[9-10]等研究了土的径向不均匀性对桩振动的影响.但由于数学上的求解困难，周铁桥等只考虑了土体分为两个圈层的情况，其划分太粗略，还难以反映桩周土径向非均质的实际情况，杨冬英虽然进行了任意圈层的计算，但计算过程太长，不利于工程应用.本文在考虑沿径向参数改变（主要是密度和剪切波速的改变），忽略土体径向位移的情况下，将桩周土分为三圈层进行了桩的振动问题研究.

1 定解问题的建立

1.1 计算简图

本文在土体为三维轴对称条件下，考虑土体竖向位移、忽略径向位移的情况下，对多圈层土中的弹性支承桩的纵向振动问题进行研究，其基本模型如图1所示.桩顶作用谐和激振力Feiωt，桩周土对桩身的侧壁切应力（摩阻力）为 f(r1,z)eiωt，桩沿侧壁对土体的反力为 p(r1,z)eiωt，其中，F、f(r1,z)、p(r1,z)及 ω分别是上述三种力的幅值和圆频率.桩长、桩径、截面积、密度、桩底弹性支承常数分别为H、r1、A、ρp、kb，三圈土体厚度、密度、土底弹性支承常数分别为 H 、ρ1、ρ2、ρ3、ks1、ks2、ks3.

1.2 假设条件

（1）每一圈层土体均各自为均质、各向同性线性粘弹性体，土体材料阻尼采用与频率无关的滞回阻尼，土层底部为弹性支承，最外圈土体径向无限延伸，土体仅有竖向位移，径向位移可忽略；

（2）桩为完全弹性、竖直、圆形等截面体，桩底部支承为弹性支承；

（3）桩土接触面两侧位移、应力连续，各圈层土的接触面两侧位移、应力连续，桩土系统为小变形谐和振动.

图1 桩土系统动力模型

1.3 定解问题

1.3.1 动力平衡方程

（1）土体动力平衡方程

设第一圈土（靠近桩的为第一圈土）、第二圈土及第三圈土中任何一点的位移为w1(r,z,t)、w2(r,z,t)、w3(r,z,t)，建立轴对称粘弹性土层纵向振动动力平衡方程如下：

由于桩土系统发生谐和振动，则位移表示为：wj(r,z,t)=wj(r,z)eiωt,代入方程（1）得到

其中：λj为拉梅常数、Gj为各自圈层土的剪切模量，λj'、Gj'为拉梅常数和剪切模量相关的粘性系数，分别为土纵向和剪切波速，μ为泊松比，Dsj=Gj'Gj和Dvj=λj'λj分别与剪应变和体积有关的滞回阻尼比，与振频无关.

（2）桩的动力平衡方程

设桩在垂直简谐荷载作用下桩身质点位移为u(z)eiωt，桩的动力平衡方程为

其中

式（4）为桩周土对桩身的侧壁切应力，m=ρpA为单位长度桩的质量，Ep为桩的杨氏模量.

1.3.2 定解条件

（1）桩周土与桩的接触界面两侧应力位移连续条件

p(r1,z)为桩对第一圈土沿侧壁的反作用力.

（2）桩的边界条件

桩顶

桩底

（3）土体的边界条件

土层顶面

土层底面

各圈土之间接触

外圈土无穷远处应力、位移为0.

2 方程求解

2.1 土体振动问题求解

采用分离变量法求解土体动力平衡问题，对第三圈土进行求解.设w3=R(r)Z(z),代入方程（2）化简得

方程（13）可分解为两个常微分方程

I0(q3r)、K0(q3r)为零阶第一类、第二类虚宗量Bessel函数.

由无穷远处位移应力为零推出A3=0；将w3=R(r)Z(z)代入土层边界条件式（9）得：C3=0；将w3=R(r)Z(z)代入土层边界条件式（10）得

其中K3=ks3HEs3为土层底部支撑刚度的无量纲参数.

至此，得到外圈土层振动的幅值表达式为

其中Bn为一系列代定常数.第三圈土对第二圈土的侧壁切应力为

K1(q3nr3)是一阶第二类虚宗量Bessel函数.

同理可以得到第二圈土体的解

及第二圈土对第三圈土的侧壁切应力、第二圈土对第一圈土的侧壁切应力

进一步可得第一圈土的方程解

及第一圈土对第二圈土的侧壁切应力、第一圈土对桩的侧壁切应力

根据第二、三圈土位移、应力连续可得

根据第一、二圈土位移、应力连续可得

根据固有函数cos(h2nz)的正交性：

对于式（27）、（28）方程两边分别乘以 cos(h2nz)，然后[0，H]积分，对于式（29）、（30）则乘以 cos(h1nz)，然后[0，H]积分. 最后得

2.2 桩振动问题求解

将公式（26）代入桩振动方程公式（3）

化简式（35）得

上述方程（36）对应的齐次方程的通解为

令方程式（36）的特解为

其中：

利用连续条件公式（5）得

利用固有函数cos(h1nz)的正交性（40）得

根据式（31）、（32）、（33）、（34）、（41）可得 An、Cn、Dn、En、Bn.至此得到桩的位移幅值表达式

式中：

其中

桩顶位移频率响应函数（即位移导纳函数）为

其中

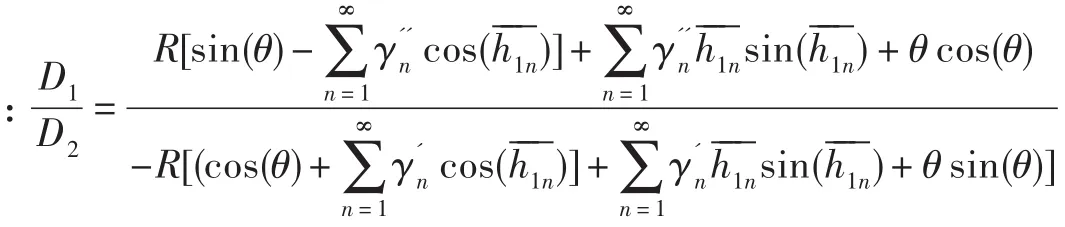
桩顶的速度频率响应函数（即速度导纳函数）为

定义桩顶位移复刚度（即位移阻抗函数）

这里k'为桩顶复刚度（阻抗）无量纲因子根据傅立叶变换性质，由H'v得到单位脉冲激励的时域响应为

式中t'=t/Tc为无量纲时间.由卷积定理可得任意激振力 f(t)作用下桩顶的时域响应

式中F(iω)是 f(t)的傅立叶变换.

式中

T'=T/Tc为无量纲脉冲宽度因子.

3 与前人解的对比

文献[7]的解是本文桩周土为均质的特殊情况，而文献[9]的解中两层土参数取为一致时即为文献[7]的解.本文对于各圈土层参数取为一致时即退化为文献[7]的解.图2与图3显示了本文解与文献[7]、文献[9]相对比的情况.证明了本文解可以退化为文献[7]、[9]的解，得到的解析结果是正确的.

图2 桩顶速度导纳曲线

图3 桩顶反射波曲线

4 结语

（1）在三维轴对称条件下，考虑土体沿径向主要参数变化，把桩周土分为三圈，在仅考虑土体竖向位移的情况下，建立在垂直简谐振动情况下弹性支承桩与滞回阻尼土体耦合作用的定解问题，得到了相对严格的桩顶频域响应解析解及时域响应半解析解.

（2）与前人成果对比表明，本文成果能退化成桩周土均质的情况，以及桩周土分为两个圈层的情况，证明了本文解的正确性和合理性.

[1]Koten H Van,Middendorp P,Brederode P Van.An analysis of dissipative wave propagation in a pile[C]//Stockholm:Seminar on the application of Stress-Wave Theory on Piles,1980.

[2]Wang T,Wang KH,Xie KH.An analytical solution to longitudinal vibration of a pile of arbitrary segments with variable modulus[J].Acta Mechanica Solida Sinica,2001,14(1):67-73.

[3]王奎华.成层广义Voigt地基中粘弹性桩纵向振动分析与应用[J].浙江大学学报:工学版，2002，36（5）：565-571，595.

[4]Novak M,Youpele O.Beredugo,Vertical Vibration of Embedded footings[J].Soil Mechanics and Foundation Division,ASCE,1972,98(SM12):544-546.

[5]Novak M.Vertical vibration of floating piles[J].Journal of the Engineering Mechanical Division,ASCE,1977,103(EM1):153-168.

[6]Novak M,Toyoaki N,Fakhry A E.Dynamic soil reaction for plane strain case[J].Journal of the Engineering Mechanical Division,ASCE,1978,104(EM4):953-959.

[7]胡昌斌，王奎华，谢康和.考虑桩土耦合作用时弹性支承桩纵向振动特性分析及应用[J].工程力学，2003，20（2）：146-154.

[8]王奎华，阙仁波，夏建中.考虑土体真三维波动效应时桩的振动理论及对近似理论的校核[J].岩石力学与工程学报，2005，24（8）：1362-1370.

[9]周铁桥，王奎华，谢康和，等.轴对称径向非均质土中桩的纵向振动特性分析[J].岩土工程学报，2005，27（6）：720-725.

[10]杨冬英，王奎华.任意圈层径向非均质土中桩的纵向振动特性研究[J].力学学报，2009，42（2）：243-252.