基于分享度的最小连通支配集求解算法
赵学锋,陈祥恩
(西北师范大学 a. 计算机科学与工程学院;b. 数学与统计学院,兰州 730070)
1 概述
支配集问题在无线网络设计、社交网络和Web 图中有许多应用和研究[1-2]。无线传感器网络(Wireless Sensor Network,WSN)中节点往往随机散落在区域中,具有相同的通信半径,常用单位圆盘图(Unit Disk Graph,UDG)作为研究网络的基本模型,所关注的问题如构建虚拟骨干网、网络分簇和拓扑控制等都与UDG 的连通支配集(Connected Dominating Set,CDS)有关。在UDG 类拓扑结构上构造最小连通支配集(Minimum Connected Dominating Set,MCDS)是NP 难题,而出于无线网络中节点计算能力和能量消耗等因素的考虑,MCDS 算法应具有分布式、局部化的特性。文献[1]提出邻居指定的局部化算法,从节点的多点中继集合中选定几个支配节点,这类算法得到的CDS 规模较大。在基于支配树的MCDS 算法中,较常见的是2 阶段构造方式,即首先构造极大独立集,然后另外选择一些连接点共同组成CDS[3-4],文献[4]给出了这类算法的近似比为7.6。文献[5]将2 阶段合为一个阶段,在与上一轮选出的支配点相距2-跳的节点中选出新的支配点,并由与新旧支配点相距1-跳的节点连接,生成网络的支配树。文献[6]在广度优先搜索树上构造分层的支配集,然后通过相邻层的中间节点将不连通的支配点连接为一个支配树,除了CDS 的大小外,还提出了以支配树的平均跳数距离(Average Hop Distance,AHD)作为新的评价准则,AHD 小,则网络通信的平均代价小且更可靠。在构造支配树时,需要确定节点权值和支配点的连接方式,最简单的权值是节点标识[3],但对CDS不是本质的[1],更多的研究以节点度数为主要指标[5-6],文献[7]将节点局部转发因子作为选择支配点的优先级。文献[8]计算的CDS 规模较小,但该文设计的是集中式算法,而面对无线传感器网络和大数据的复杂网络,利用局部信息求解问题成为新的要求[9],集中式算法不能适应这一要求。另外,对MCDS 的研究还延伸到一些新的问题,如文献[10]要求网络节点要被多个节点所支配,文献[11]将分享度(Share Degree,SD)作为量化指标选举网络的覆盖集。以上述内容为基础,本文提出一种基于分享度的最小连通支配集求解算法。
2 符号与概念
设N(u)={v|v∈V,(u,v)∈E}是节点u∈V 的邻接点集合;u 的度d(u)=|N(u)|;T 表示SD 算法构造的支配树;VT为T的节点集;u.prev 是u∈VT的父节点;h (u,v)表示网络G 中u,v∈V 之间最短通信链路的跳数,最大的h (u,v)称为网络直径;hT(u,v)是T 中节点u、节点v 之间唯一通信链路的跳数。特别地,当u 为T 的根节点时,将h(u,v)和hT(u,v)分别记为h (v)和hT(v);G 的AHD 的计算公式为:∑h (u,v)/n(n-1),T 的AHD 为:∑hT((u,v)/|VT|(|VT|-1),∑分别是对各自图中的所有点对求和。
定义1(UDG)n 个点随机均匀分布在区域[0,R]2上,2 点邻接⇔其欧氏距离不超过r。当R=1 时,UDG 存在临界半径rc,满足πnrc2=lnn 且对r≥rc,UDG 几乎是连通的。
定义2(SD)设节点v∈N(u),即v 是u 的d(u)个邻居中的一个成员,则v 对u 的分享度为1/d(u)。现将N(u)中度数相同的节点归为一类,设|{v|v∈N(u)∧d(v)=i}|=ki,称ki/i 为u 关于度数i 的分享度。
称fu(x)=k1x+k2x2+…+kn-1xn-1为u 的度分布,显然fu(1)=d(u)。
称gu(x)=k1x+k2x2/2+…+kn-1xn-1/(n-1)为u 的分享度分布。
设v 的分享度分布为:gv(x)=b1x+b2x2/2+…+bn-1xn-1/(n- 1)。若k1=b1,k1=b2,…,ki-1=bi-1,但ki>bi,则称gu(x)>gv(x)。
若gu(x)>gv(x)对∀v∈{w|w∈N(u)∧s(w)=0}成立,则u为局部剩余SD 最大节点,称u 是局部分享度占优的。分享度的意义在于,gu(x)越大则邻居点被支配的比例下降得越快。
节点u 的权值Q(u)=<gu(x),u>,Q(u)>Q(v)⇔(gu(x)>gv(x))∨(gu(x)=gv(x)∧u<v)。
3 基于SD 的MCDS 求解算法
3.1 算法规则与流程
SD 算法的支配树构造表示一个迭代过程,记Ai为第i 次迭代后V 中所有状态为4 的节点集合,即Ai={u|u∈V∧s(u)=4}。初始阶段,A0={I},一般情况下,Ai=SD(Ai-1),i=1,2,…,若迭代进行到Ak=∅时结束,则k 为迭代复杂度。算法可形式化地描述为一个4 元组:<G,SD,s,A0>,其中,s 为节点状态变迁,s(u)∈{0,1,2,3,4,5}。初始时只有根节点I 状态为4,其余节点状态为0。其中,1(支配点)、2(连接点)和5(退化点)为稳定状态;s(u)=3 表明u 是支配点的子节点;若没有转到状态2,迭代结束后维持3 状态不变;s(u)=4,是3 状态节点的子节点,是一个临时状态。算法的迭代运行将当前4 状态节点的状态转为{1,3,5}中的一种。对节点w∈Ai,状态变迁为4→1,表明w 在局部分享度占优;状态变迁为4→5,即w 的局部分享度为0;状态变迁为4→3,表明在w 的邻居N(w)∩Ai中新产生了1 态点u,则令w.prev=u,而N(w)中的0 态点随后转为新的4 态点,完成一次迭代。算法结束时状态为1、2 的节点组成CDS。节点的状态变迁如图1 所示,边上的数字表示接收的消息种类。

图1 节点状态变迁
基于分享度构造支配树的算法描述如下:

3.2 算法分析
在执行While 的迭代过程中依次产生的4 状态节点集合为A0,A1,…,Ak,现设相应的1 状态节点集合为D0,D1,…,Dk,显然Di是Ai(1≤i≤k)的子集且A0=D0={I},而D=D1∪D2∪…∪Dk={u|u∈V∧s(u)=1}为支配点集;C={u|u∈V∧s(u)=2}为连接点集。
定理1 SD 算法得到的是网络的支配树。
证明 迭代结束时Ak=∅意味着G 中已无4 态点,也不存在0 态点,网络节点的状态为{1,2,3,5},进入稳定状态。设第次i 迭代完成时1、2 状态节点组成了一个树,设u∈Di+1,由步骤9、步骤10,u 将选择Di与Di+1之间的一个3 态节点v 为唯一的父节点,并使s(v)=2,由于网络中的每个3 态点都是1 态点的子节点,因此存在唯一的w∈Di,使w 为v 的父节点,因此,u 通过v 与w 连接,形成一个随迭代次数增长的树。若以根节点I 为0 层,则算法结束时形成一个偶层为1 态点,奇层由2 态点组成的交错支配树T。T 的节点集VT=D∪C 为G 中MCDS 的近似解,T 的边集ET={(u,v)|u,v∈VT∧(u=v.prev)}。
引理1 设G 是n 个节点的UDG,r2=arc2,参数a>1 调节网络连通性和节点密度。记△为G 中节点的最大度数,则对常数δ≥6,以1-(1/n3a)的概率,使△≤δalnn。
证明 用D(u,r)表示以u∈V 为中心r 为半径的圆盘,则N(u)中的节点都分布在D(u,r)中,按照UDG 模型,G 中节点分布在区域[0,R]2中,当u 接近区域边界时,D(u,r)不会完全包含在[0,R]2中,相交部分的面积为Area{D(u,r)∩[0,R]2}<Area{D(u,r)}=πr2。为方便分析,令D(u,r0)是另一个圆盘,满足:r0>r 且Area{D(u,r0)∩[0,R]2}=πr2,设D(u,r0)∩[0,R]2中的节点数为μ,其期望值为E[μ]=(n-1)×πr2/R2=(n-1)×alnn/n=alnn-O(1),于是:
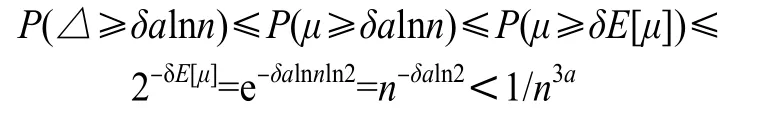
其中,第3 个≤依据的是文献[12]的定理4.4。
网络中节点的期望度数为alnn,引理1 说明G 中节点度数超出alnn 较大倍数几乎是不可能的,因此,在下面的分析中将G 中节点度数看作alnn。
定理2 SD 算法的时间复杂度为O(nlnn)。
证明 控制算法运行时间关键步骤是支配点的选举。∀u∈D,需要收集邻居点v∈A∩N(u)的Q(v)=<gv(x),v>,并与自己的权值Q(u)=<gu(x),v>比较,因此,在u 上选举的时间代价最多为O((lnn)2),从而算法的执行时间为O(|D|(lnn)2)。由于V 随机分布在[0,R]2中,G 的支配集大小由[0,R]2中所能填充的半径为r/2 的圆盘数量决定,即|D|≤1/(π(r/2)2)≤4n/lnn,因此|D|(lnn)2≤4nlnn,即结论成立。
引理2 ∀u∈Di,∀v∈Di-1,1≤i≤k,成立h(u)≥h(v)+1。
引理3 ∀u,v∈Di,1≤i≤k,成立hT(u)=hT(v)。
定理3 ∀u∈Di,1≤i≤k,成立hT(u)≤2h(u)。
证明 依归纳法证明。当i=1 时,hT(u)=h(u)=2,符合;假设结论对i(≥2)成立,考虑i+1 的情况。∀u∈Di+1,如果u.prev∈Ai-Di,则u.prev 的状态变迁为0→4→3,则∃v∈Di为u.prev 的更新后唯一的父节点,这时hT(u)=hT(v)+2,按照归纳假设,hT(v)≤2h(v),所以,hT(u)≤2h(v)+2=2(h(v)+1)=2h(u);如果u.prev 的状态变迁为0→3,此时,hT(u)=hT(v)+2≤2h(v)+2=2h(u)-2<2h(u)。这表明T 中从根节点I 开始的每条路径长度不超过网络直径的2 倍。
4 实验结果与分析
本文算法用Java 语言实现。为验证其有效性,在UDG上进行了实验,并与文献[6]的CDS-BD-C2 算法进行比较,以文献[8]集中式算法——BCOP 算法作为MCDS 测试基准。每个实验数据都是在随机产生的100 个连通网络拓扑图上运行结果的均值。2 组实验数据如下:
(1)节点数n 从300 开始以增量100 变化至900,区域边长R=500 m,通信半径r=50 m,CDS 中的点数随网络节点数的变化如图2 所示,平均跳数距离随节点数的变化如图3 所示。随着节点数的变化,本文算法的计算结果总是保持较优。

图2 CDS 中的点数随网络节点数的变化
(2)节点数n=1000,R=100 m,半径r 以5 为步长从10 m 增加至40 m,随着r 的增大,网络密度逐渐增加。CDS中的点数随网络通信半径的变化如图4 所示,平均跳数距离(Average Hop Distance,AHD)随网络通信半径的变化如图5 所示,在较为稀疏的网络中,本文算法有明显的优势。

图4 CDS 中的点数随网络通信半径的变化
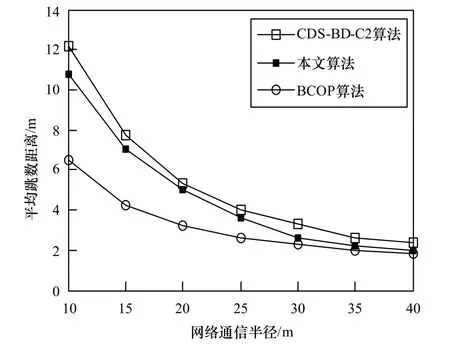
图5 平均跳数距离随网络通信半径的变化
上述实验结果中的G-AHD 表示图G 的AHD,是任何支配树的AHD 下界,在此作为算法比较的参照。综合2 组实验的数据进行对比分析可见,在不同的网络参数下,无论是CDS 的大小还是支配树的平均跳数距离,这2 个性能指标上本文算法都对CDS-BD-C2 算法有所改进,构造的支配树的平均跳数距离平均减少12%,得到的CDS 更接近BCOP 算法。
5 结束语
本文提出一种基于分享度求解最小连通支配集的SD 算法。从根节点开始迭代交替选择支配点和连接点,支配点的选取主要依赖于1-跳邻居中0 状态节点分享度的比较。连接点将本次生成的支配点和上次产生距根节点近的支配点连通起来,使得所有选择出的具有局部分享度占优的节点恰好是连通的。算法具有分布式特点,由1 个阶段完成构造,避免了2 次构造的通信开销。在UDG 模型上分析了时间复杂度和支配树的特性。实验结果表明,和现有构造支配树的分布式相比,该算法得到的CDS 点数较少,支配树的平均跳数也比近期具有代表性的CDS-BD-C2 算法计算得到的值小,便于实际应用。研究新的节点权值和连接方式,以网络局部信息改进MCDS 算法的性能是今后的研究重点。
[1]Wu Jie,Lou Wei,Dai Fei. Extended Multipoint Relays to Determine Connected Dominating Sets in MANETs[J]. IEEE Transactions on Computers,2006,55(3): 334-347.
[2]Cooper C,Klasing R,Zito M. Lower Bounds and Algorithms for Dominating Sets in Web Graphs[J]. Internet Mathematics,2005,2(2): 275-300.
[3]Wan Pengjun,Alzoubi K M,Frieder O. Distributed Construction of Connected Dominating Set in Wireless Ad Hoc Networks[J]. Mobile Networks and Applications,2004,9(2):141-149.
[4]Wu Weili,Du Hongwei,Jia Xiaohua,et al. Minimum Connected Dominating Sets and Maximal Independent Sets in Unit Disk Graphs[J]. Theoretical Computer Science,2006,352(1-3): 1-7.
[5]Funke S,Kesselman A,Meyer U. A Simple Improved Distributed Algorithm for Minimum CDS in Unit Disk Graphs[J].ACM Transactions on Sensor Networks,2006,2(3): 444-453.
[6]Kim D,Wu Yiwei,Li Yingshu,et al. Constructing Minimum Connected Dominating Sets with Bounded Diameters in Wireless Networks[J]. IEEE Transactions on Parallel and Distributed System,2009,20(2): 147-157.
[7]解文斌,李 佳,鲜 明,等. 基于拓扑特性的分布式虚拟骨干网算法[J]. 软件学报,2010,21(6): 1416-1425.
[8]Butenko S,Cheng Xiuzhen,Oliveira C,et al. A New Heuristics for the Minimum Connected Dominating Set Problem on Ad Hoc Wireless Networks[C]//Proc. of Recent Developments in Cooperative Control and Optimization. New York,USA:Kluwer Academic Publisher,2004.
[9]Borgs C,Brautbar M,Chayes J,et al. The Power of Local Information in Social Networks[C]//Proc. of the 8th International Conference on Internet and Network Economics.Berlin,Germany: Springer,2012.
[10] Wang Feng,Du Hongwei,Camacho E,et al. On Positive Influence Dominating Sets in Social Networks[J]. Theoretical Computer Science,2011,412(3): 265-269.
[11] Li Shaohua,Wang Jianxin,Chen Jianer,et al. An Algorithm for Minimum Vertex Cover Based on Max-I Share Degree[J].Journal of Computers,2011,6(8): 1781-1788.
[12] Mitzenmacher M,Upfal E. Probability and Computing:Randomized Algorithms and Probabilistic Analysis[M].Cambridge,UK: Cambridge University Press,2005.

