码垛机器人的轨迹规划与仿真分析*
叶辰雷,刘晓平,贠 超
(1.北京邮电大学自动化学院,北京 100876;2.北京航空航天大学机器人研究所,北京 100191)
码垛机器人的轨迹规划与仿真分析*
叶辰雷1,刘晓平1,贠 超2
(1.北京邮电大学自动化学院,北京 100876;2.北京航空航天大学机器人研究所,北京 100191)
针对码垛机器人在高速运行过程中产生的冲击问题,以优化运行节拍提高效率为目的对码垛机器人的运动轨迹进行规划。利用笛卡尔空间圆弧插补方法对运行轨迹进行优化,并在此基础上利用三次曲线插补对r关节运动轨迹进行了再次修正,基于Matlab建立模型对规划结果进行了仿真。结果表明通过轨迹曲线规划方法使得码垛机器人在运行过程当中满足了减小运行冲击和提高运行效率的要求。
码垛机器人;轨迹规划;圆弧插补;仿真曲线
1 引言
码垛机器人技术作为自动化物流技术的重要环节,对于提升生产效率,降低市场成本,推进生产方式现代化有着重要意义。码垛机器人对于响应时间和冲击力的控制只有在相对应的运动轨迹之下,才能同时保证运动速度的高效和机械本体所受到冲击最小。
通过进行有效地轨迹规划,对于保障运行过程中的运动平稳和时间要求[1],提高码垛机器人的运行效率和稳定性起着关键性的作用,笔者采用笛卡尔空间圆弧圆的滑过渡方法来保证运动轨迹路径的规划,圆弧轨迹在运动过程中避免了冲击,在空间轨迹规划之后又对规划结果利用三次曲线插补的关节轨迹规划做了二次修正,针对课题要求的运动轨迹结合实际运动规范进行了理论推导,根据相关理论推倒的结果联合Matlab编程给出了数学仿真数据结论,验证了规划方案的可行性。
2 码垛机器人的结构和运动轨迹
2.1 码垛机器人的设计结构
码垛机器人的结构其具体结构如图1所示,该机器人的手臂,固定在腰部上,在该部分内小臂通过前大臂、后大臂与的搬运和码垛作业,且机械系统主要有4个关节部分组成,能实现四种运动:腰部旋转,大臂上下运动,小臂前后运动和手腕回转运动四种运动,全部由交流伺服电机驱动。
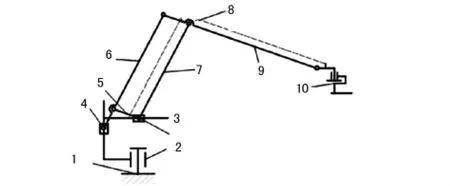
图1 机器人机构简图
2.2 码垛机器人的运动
对于自由度大于3的常规工业机器人而言,其运动参数的设计及计算不唯一[2]。本文涉及的码垛机器人所采用的是基于“取-放”这一工作模式的要求进行的设计,实际工作情况下采取的是“4-3-4”的工作模式。即刚开始时位于初始位置O,抓取时抓手位于流水线上方位置等待抓取这一位置为抓取准备点P2,当有货物来到时从P2点垂直向下运动至抓取点P1,抓取货物,之后返回P2位置再进行下一步的动作,垂直提升一段距离以确保做搬运运动时抓手不与流水线运输带发生碰撞;之后由抓取准备点P2向放置准备点P3做水平运动;再由P3点向预先计算的放置点P4做垂直运动到达之后抓手打开,货物按一定姿态放置于垛型之中。其中P3、P4是根据垛型不同位置,每次放时重新计算生成的点,如图2所示。
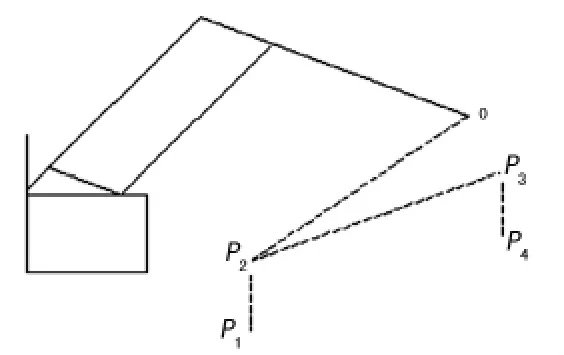
图2 码垛机器人的运动示意图
2.3 码垛机器人实际运动轨迹
码垛机器人堆垛的过程,在堆垛过程当中,机器人运行采用点到点运行,即采用PTP的方式,即只需要确定各段运动轨迹的端点,而端点之间运动轨迹由各轴电机独立控制,因此实际运动曲线在空间当中并不是如示意图中的折线,而是随机的曲线,同时由于在必须到达准备点这一要求,在准备点处极有可能形成锐利的夹角,在实际空间运动中对于机械结构和电机都会构成较大的力和扭矩的冲击,会造成机械本体的震动同时又影响到运行速度和节拍。实际运动曲线如图3所示。
3 轨迹规划的理论方法及规划方案的确定
实际运动过程当中码垛机器人运动的目标点是依据两方面构成的:首先是控制试教点位置确定抓取点以及放置点;其次是通过计算得到抓取准备点的位置和第一放置准备点,以及通过垛型规划计算确定的其余放置点。因此在每次行程工作中码垛机器人的运动都是由前文中提供P1、P2、P3、P4四个点位置构成的,在轨迹设计当中有以下要求:①轨迹必须包含4个位置点;②避免锐利的转角和折线,在空间内行程应当是一条圆滑曲线;③通过插补的方式确保所有点到点的距离相等。
综合上述三点,通过空间4点位置插补两段圆弧,根据设定的运动轨迹方程计算符合要求的插补点坐标,通过坐标转换将空间轨迹转化为关节的运动轨迹,将转换的圆柱坐标发送至PMAC卡,执行运动程序实现轨迹的规划。由图4可知,4个点构成的三条直线位于同一平面内,由于P2与P3两点作为准备点,必须通过,因此在轨迹规划中增加两点Pa与Pb,其坐标位于准备点z轴坐标上方。对直线与直线的连接处做圆弧插补要求既要圆弧位于同一平面内,又要求圆弧与直线的切点在z轴方向上不小于准备点。
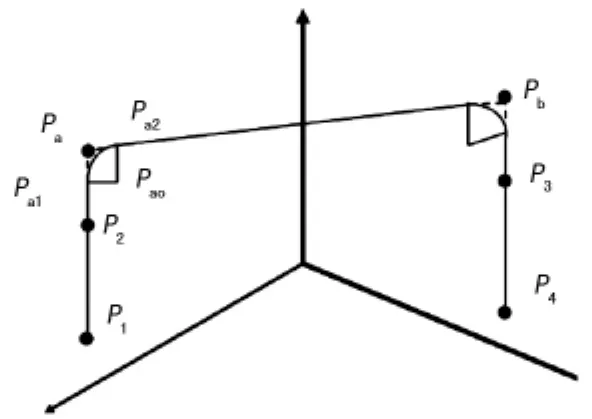
图4 轨迹规划曲线
4 轨迹插补的理论推导及计算
4.1 空间圆弧轨迹的插补
4.1.1 圆弧位置点的计算
已知空间不共线三点坐标,求由三点组成的两条线断的插补圆弧情况如图5所示,插补圆弧要求已知空间三点P1(χ1,y1,z1),P2(χ2,y2,z2),P3(χ3,y3,z3)三点分别构成的两条直线,假设圆心点坐标为Po(a,b,c),根据空间能不共线的三个点可以确定一个平面可确定方程为:
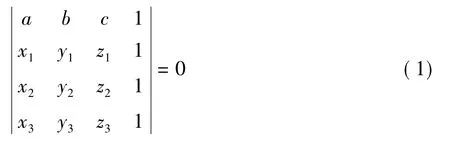
同时假设圆弧的起始点Pa(χa,ya,za)和终止点Pb(χb,yb,zb)。根据过度圆弧的圆心到切点的距离等于半径r,可联立方程组:
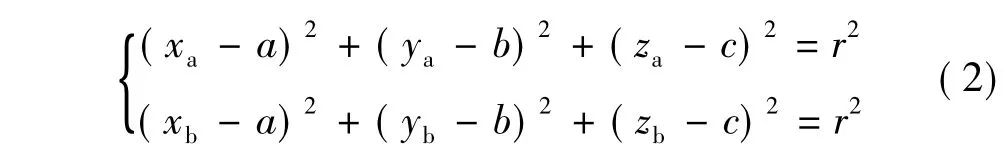
又可知,过度圆弧的圆心与切点的连线垂直于相切直线,可联立方程组:
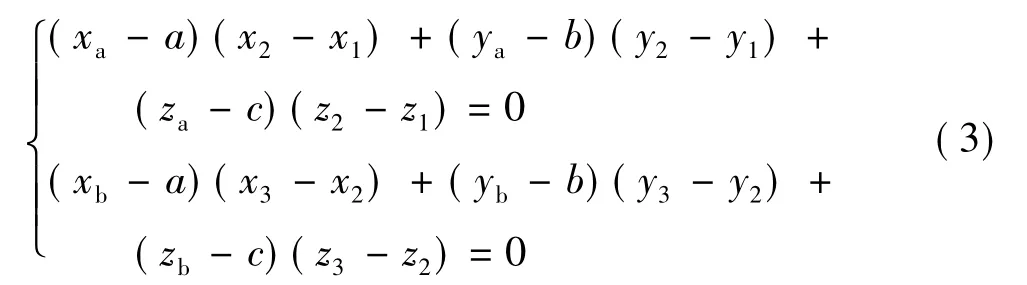
通过上述5个方程可以求解,由于需要求解的变量有Po(a,b,c)、Pa(χa,ya,za)和Pb(χb,yb,zb),共有9个未知量,因此还需要再引入两个比例系数来表示切点坐标。已知 Pa与 Pb分别位于线段 P1P2和P2P3上,引入两个比例系数k1和k2,这样就可以将Pa(χa,ya,za)和Pb(χb,yb,zb)的六个未知量用k1和k2及P1(χ1,y1,z1),P2(χ2,y2,z2),P3(χ3,y3,z3)来表示。并且从图中可知,切点始终位于线段两点之间,因此要求将0<k1<1和0<k2<1作为筛选条件,最终得到圆心坐标和两个切点的坐标值。
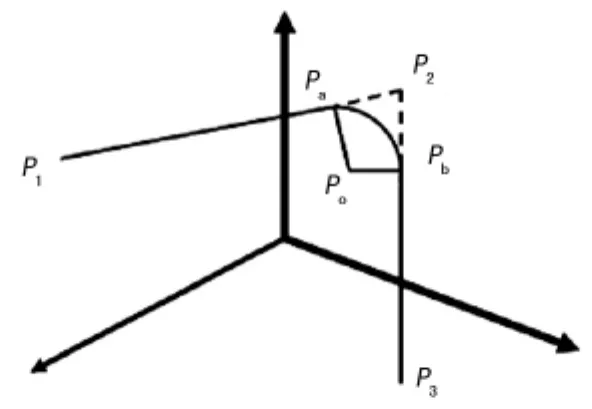
图5 圆弧位置计算示意
4.1.2 圆弧插补的计算推导
通过已知起始点,终止点和圆心点的坐标,同时根据已设定的半径插补圆弧上的距离求取插补点坐标。
(1)确定所要插补圆弧点的数量,以给定各个点之间距离l,通过计算个点之间圆弧段距离判断圆弧所需要插补点数量,首先由圆弧起始点点原点终止点所构成的弧如公式S=θr所得,通过均分计算计算所需插补点N=S/l,为确保插补足够数量向上取整数。
(2)通过向量求出圆弧插补方向通过已知起始点A终止点C及圆弧圆心B,可以利用≤90°来表示圆弧所在平面的法向量n,由于所得插补圆弧始终插补于两条直线之间,所以可以得知∠ABC≤90°,由于法向量方向由右手定则确定,具体方法是右手拇指与其余四指垂直,握拳时四指运动的方向表示从第一向量到第二向量,拇指所指方向就是法向量的方向。确定插补总是以法向量方向沿顺时针方向,因此只需要确定圆弧起始点与终止点位置利用插补方程计算插补点坐标。如图6所示,在A为起始点C为终止点的情况下,法向量的顺时针沿A指向C;反之法沿C指向A,因此在不同的环境下都可以表示出圆弧所要插补圆弧的移动方向。
(3)根据圆弧插补递推方程插补圆弧并修正误差通过圆弧起始点、圆心和终止点确定圆弧向量方向,在做切向插补递推时,可以看出在做切向运动的,如图7所示。
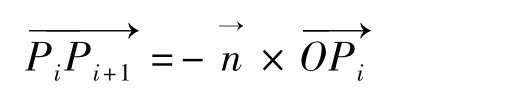
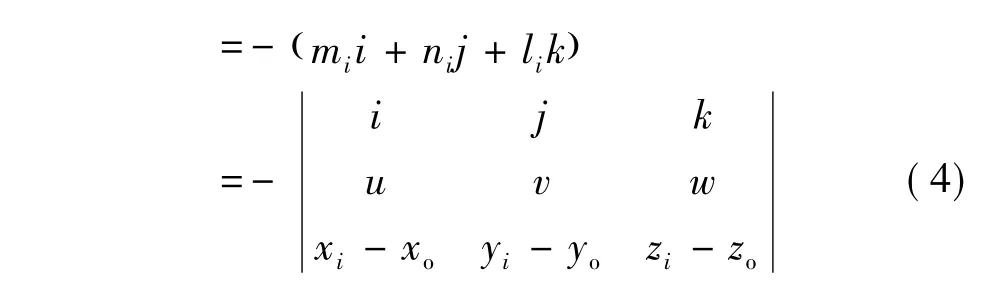
其中所得(mi,ni,li)为切向进给方向,根据切向距离l可以求出切向运动的位置坐标Pi+1'如下:

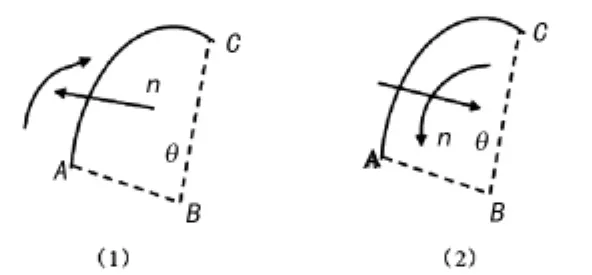
图6 圆弧方向的确定
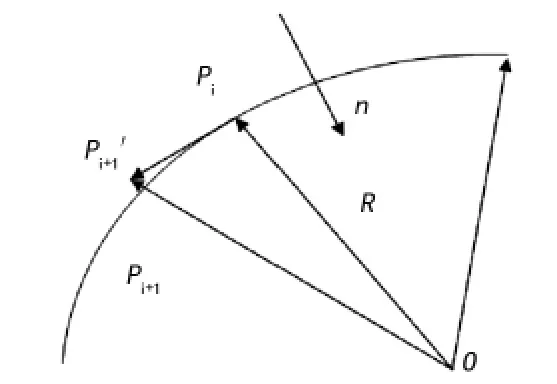
图7 圆弧递推插补示意

可以通过公式计算出每个插补点的空间位置坐标,此种插补方法插补点总在圆弧上,不存在累积误差,但由于存在插补点不能再到达终止点时确定插补到位,存在最终插补点偏离终止点的问题,因此对于终止点的位置进行修正,用计算所得的终止点坐标替换插补递推点的坐标,确保插补点的位置在所要求的范围之内。
4.2 空间直线轨迹的插补
首先要确定直线坐标的起始点A和终止点B根据要求的点和点之间的距离要求l来先确定插补点的数量,通过求取两点间的距离可以得到的直线距离;其次对于距离求取点的个数并且取上限,同时利用等比例插补的原理分别求出插补点的空间坐标,其计算公式如下:
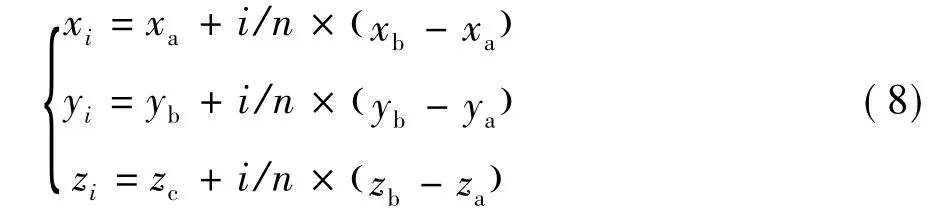
其中:i表示各个点n表示所插补点的总数量。最后利用替换最后一点为给定终止点确保插补点的位置信息位于规划轨迹范围内。
5 轨迹的仿真分析及二次修正
5.1 规划轨迹的仿真和分析
根据上述方法可以求出规划轨迹插补点的空间坐标,利用这些点使用Matlab可以绘制出仿真空间轨迹如图8所示图中曲线所取插补圆弧半径r=50 cm,插补点间距l=10 cm。图中黑色的轨迹为原轨迹,圆点为规划轨迹。可以证明在货物提升之后到货物搬运过程的曲线由之前的尖锐夹角过渡成为平滑的圆弧,避免了由于尖锐过度造成的问题。
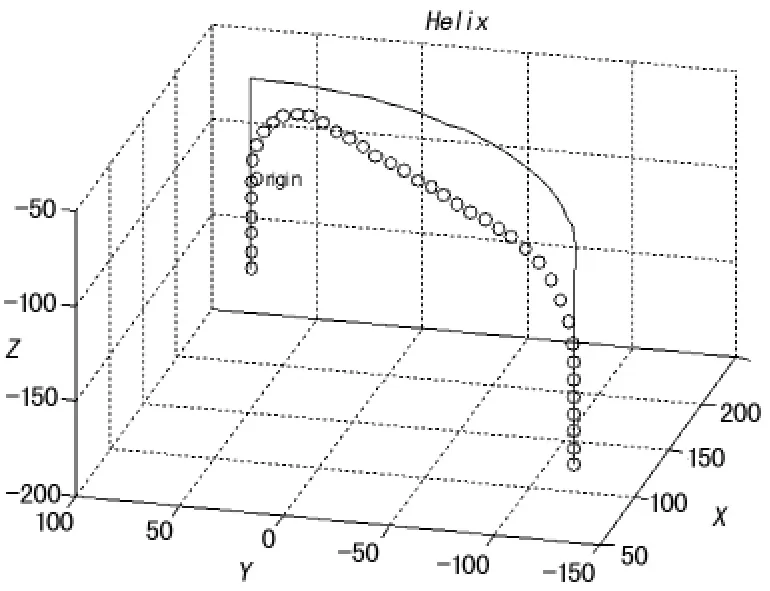
图8 轨迹规划空间曲线
对于码垛机器人运动,其关节运动直接关系到电机选型及运动速度极限问题,通过坐标系的转化和运动学反解,我们可以通过笛卡尔坐标系运动轨迹点得到控制位置的三个电机的关节运动曲线运动情况,如图9为轨迹仿真曲线。
码垛机器人作为一种点对点的搬运机器设备,在实际运动中被关心的更多是运动速度和运动起始与终止位置。在规划运动曲线图9中可以看出在实际关节运动过程中在r轴方向上的运动相较于未进行规划的运动在运动曲线上更加平滑,但同时也可见其运动速度曲线绝对幅值变大,造成这一变化的原因是由于插补轨迹曲线是利用4个点坐标来确定的曲线坐标,而曲线位于四个点所构成的平面内,而码垛机器人的运动坐标系是柱坐标系,变量θ对应柱坐标系中的偏转角,关节变量χ对应柱坐标系中的距离在轴距离r,关节变量z对应柱坐标系当中z。因此在实际运动情况下,我们分别考虑三个关节运动曲线的实际情况。由规划曲线我们可以看出:根据现有轨迹运动,r值得变化存在一个先变小后变大的过程,这个过程实际上对于电机运转是多余的,而会引起加减速过程从而减缓运动速度。
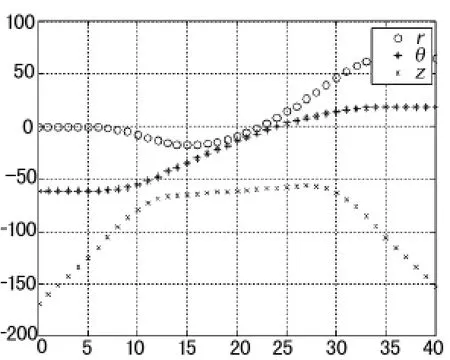
图9 轨迹规划关节曲线
从上述原因所导致的结果——在实际运动中所做的运动路程更长,速度变化也更大。这点不符合轨迹规划要求运动结果时间优化的要求,而更大的运动变化同时也会造成更明显的震动和冲击,考虑到上述问题,有必要对 r关节的运动曲线进行重新规划[5-6]。
5.2 利用三次曲线插补的二次修正计算
对于上述问题本文利用三次曲线插补的方法进行处理。三次曲线具有二阶可导性,其表达方式保证了其一阶求导结果即速度曲线平滑和二阶求导结果即加速度曲线的连续性,在原有插补点基础上可以保证所得结果符合路程运动和速度曲线的要求。
(1)三次曲线方程 已知给定数量的插补点n,对于各个位姿点的变化量为Qi(i=1,2,……,n),各连续点的运动时间为ti(i=1,2,……,n)其间隔时间为T。由上述已知量可以推导出插补曲线的方程为:

在修正曲线的计算当中,规划的曲线是基于之前所得到的插补点进行的,即修正曲线插补点的数量与之前插补点的数量为一一对应的关系,因此在计算过程中,公式ti=n×T,其中T为确定插补点时间间隔常量。当确定了插补点的坐标位置要求、速度要求和插补点要求,可得到所求三次曲线方程[7-8]。
(2)求解三次曲线方程系数 根据本文中所涉及的关节空间轨迹修正方法,对于方程插补确定起始点位置坐标Q1(t1)和速度Q1'(t1)以及终止点的位置坐标Qn(tn)和速度Qn'(tn)可得到方程组:
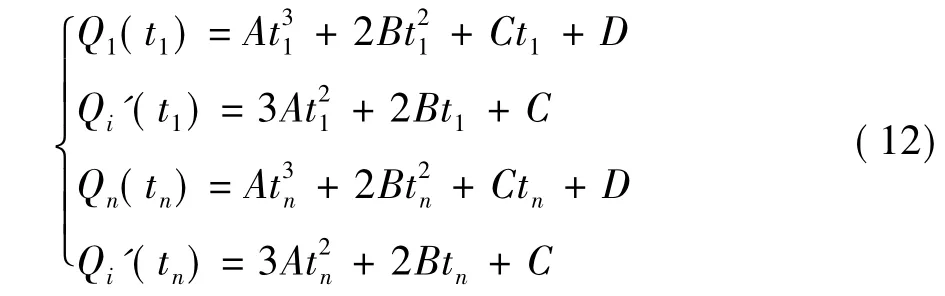
规划中胜定速度在起始点和终止点皆为0,因此由方程式(12)可以求出所需要的A、B、C、D四个未知量以确定三次曲线的方程,且通过已知的三次曲线修正之前的r位置坐标各个点,从而达到对轨迹规划曲线的二次修正。
5.3 修正后的仿真及分析
根据上文所提供的算法结合仿真数据对插补轨迹曲线做修正将位于规划平面内的插补曲线做出二次轨迹修正规划。最后得到轨迹空间运动曲线仿真如图10所示。
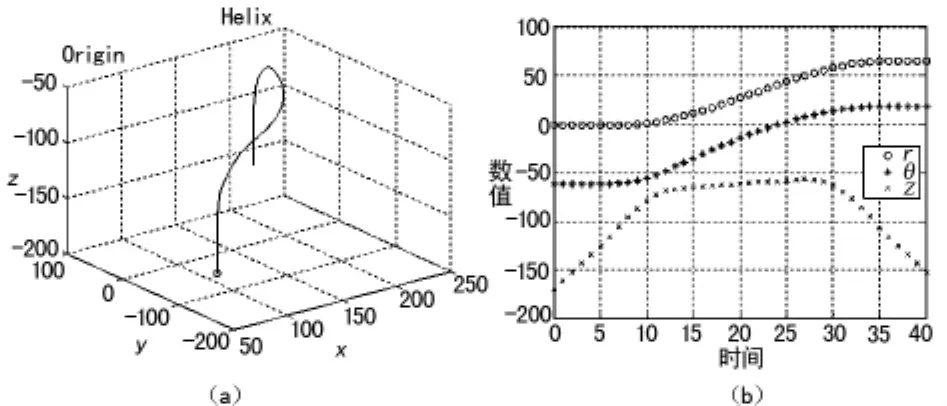
图10 轨迹规划空间及关节运动曲线
通过关节运动轨迹图10可以看出,r关节轨迹运动满足要求,不再出现富余运动。速度曲线图也显示速度变化更加平稳,幅值变化不大。
6 结论
通过对空间机器人运动轨迹规划方法结合码垛机器人的自身特点和实际运动需求进行设计的轨迹规划方案,利用直线插补和圆弧插补计算结合数学算法和规划要求推导计算公式;从而得到了插补点的空间轨迹位置集合。通过利用Matlab数学计算工具对计算方案进行了模拟仿真,通过比较仿真结果针对相关规划曲线做了二次修正,验证了修正结论的可行性,证明轨迹规划的相关要求。对于提高码垛机器人的运动效率减小运行中的冲击振动问题起到了重要作用。
[1] 蔡自兴.机器人学[M].北京:清华大学出版社,2009.
[2] 马香峰.机器人机构学[M].北京:机械工业出版社,1991.
[3] 原 魁.工业机器人发展现状与趋势[J].工厂自动化,2007,1(1):34-38.
[4] 余达太,马香峰.工业机器人应用工程[M].北京:冶金工业出版社,1999.
[5] 胡洪国,高建华.码垛技术综述[J].组合机床与自动化加工技术,2000(6):7-9.
[6] Zlajpah L,Nemec B.Implementation of time-optimal path-tracking control on palletizing robots[C]//Industrial Electronics,1999.ISIE'99.Proceedings of the IEEE International Symposium on.IEEE,1999(2):861-866.
[7] Lin C,Chang P,Luh J.Formulation and optimization of cubic polynomial joint trajectories for industrial robots[J].Automatic Control,IEEE Transactions on,1983,28(12):1066-1074.
[8] 陈 航,殷国富,赵 伟,等.工业机器人模块化设计研究[J].机械,2009(3): 57-59.
Trajectory Planning and Simulation for Palletizing Robot
YE Chen-lei1,LIU Xiao-ping1,YUN Chao2
(1.School of Automation,Beijing University of Posts and Telecommunications Institute of Automation,Beijing 100876,China; 2 Robotics Institute,Beihang University,Beijing 100191,China)
Aiming at the impact problems at the process of high-speed operation of the palletzing robot,trajectory of palletizing robot is planned in order to optimize operational tempo and improve the efficiency.Arc interpolation methods are used to optimize running track in a Cartesian coordinate system.On this basis,r-joint trajectory is corrected secondary using cubic spline interpolation,the planning conclusion is simulated based on Matlab model.The results show that palletizing robot operation meets the requirements of reducing impact and improves the operation efficiency by this trajectory planning method.
palletizing robot;trajectory planning;circular arc interpolation;simulation curve
TP242
A
1007-4414(2013)05-0026-05
2013-09-03
叶辰雷(1988-),男,云南昆明人,硕士,主要从事测控技术与结构动态设计方面的研究。

