UPQC最小化视在功率补偿策略研究

陈辰，夏益辉，李哲

(1. 海军装备技术研究所，北京102442；2.海军工程大学电气工程学院，武汉市 430033)

0 引言

统一电能质量控制器[1-4](UPQC，Unified Power Quality Conditioner)在补偿电压跌落和负载谐波(无功)电流时，串、并联部分将会与整个电力系统交换有功功率和无功功率，考虑到电压跌落幅度和无功电流的大小可知UPQC的功率需求是不容忽视的。对UPQC的功率分析一方面可深入研究串、并联部分与系统的功率交换关系，为确定IGBT等开关管的电压、电流等级提供依据；另一方面对不同补偿策略下的功率需求分析也为补偿策略的选择、优化提供了可能。

目前对UPQC补偿策略及功率需求分析的研究主要是在串联有源滤波器(DVR)和并联有源滤波器补偿策略的基础上进行的，但考虑对无功功率的协调补偿时，其补偿策略和功率需求分析又有所不同。文献[5]分析了采用最小有功的补偿方式，文献[6]在串联滤波器额定容量允许的情况下，控制补偿电压的注入角，使得串联部分承担了一部分无功补偿的任务，扩大了UPQC补偿无功功率的范围。

本节从UPQC与整个电力系统的功率交换的角度出发，建立了UPQC不同补偿策略下统一功率模型，分析了各补偿策略下UPQC内部及其与系统有功功率和无功功率的交换关系，研究了不同补偿策略对系统稳定的影响并提出采用最小化视在功率补偿策略来减小整个UPQC的容量，有效提高系统稳定运行的安全性并降低了系统损耗。

1 UPQC的基本数学模型

图1是所研究的三相三线统一电能质量控制器的主电路图，其中串联侧通过三个隔离变压器以Y/Y方式串联接入主电路，并联部分直接并联接入负载侧，串联部分和并联部分均采用基于IGBT的三相全控桥，相互之间通过直流侧电容连接。

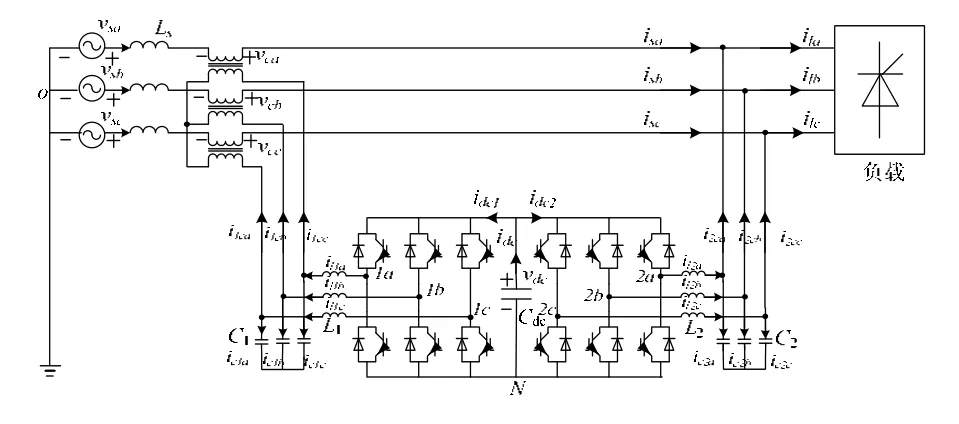
图1 UPQC的基本电路结构

2 UPQC不同补偿策略分析

并联有源滤波器常见的补偿策略是单独补偿负载电流中的谐波分量或同时补偿谐波分量和无功分量。由于谐波电流产生的有功功率和无功功率相对于基波电路产生的有功功率和无功功率是非常小的，因此，并联部分的补偿策略是同时补偿谐波电流和无功电流。

串联有源滤波器的主要任务是补偿电源侧电压的跌落、波动、谐波等电能质量问题，其基本目标是保证负载侧电压的稳定。若仅考虑补偿基波电压的跌落，则串联有源滤波器的功能与动态电压恢复器(DVR)的功能是一致的，因此其补偿策略与DVR补偿策略是一致的，其补偿策略(如图2所示)主要有：

1）最小电压补偿。补偿电压和系统电压、负载电压同相，负载电压相位始终跟随系统电压的相位，在图中以VDVR1表示；

2）完全补偿。即通过补偿使得电压的幅值和相位都恢复扰动出现前的水平(V)，在图中以VDVR2表示；

3）最小能量补偿。在保证负载电压幅值达到扰动前水平时，补偿电压与系统电流产生的有功功率最小，即串联滤波器输出的有功功率最小，在图中以VDVR3表示。

图2 DVR电压补偿策略示意图

将串联部分的补偿策略和并联部分的补偿补偿策略结合起来，即可对整个UPQC的补偿策略进行分析。

图3 UPQC补偿向量示意图

以图3所示的向量图来说明补偿策略。图中：Vs为网侧电源电压、VL为负载侧电压、Vc为串联部分补偿电压、Is为系统电流、IL为负载电流、IC为并联部分补偿电流、α为负载侧电压超前电源电压相角、β为串联侧补偿电压超前电源电压相角、γ为负载基波电流相对于负载电压的滞后相角、θ为负载基波电流相对于电源电压的超前相角。

以下标1、2表示电压跌落前后的电压、电流变量。若电压跌落幅度相对于参考电压为(1-k)，则跌落后电压有效值的幅值为：

由于电压跌落前后负载需要的功率不变，因此可得：

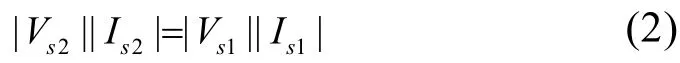
由式 (1) 和式(2)可得：

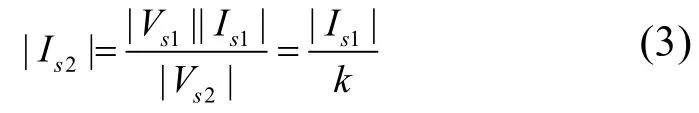
UPQC正常工作时，电压跌落前后负载侧电压幅值应保持不变，因此负载电流的幅值也保持不变，因此可得：

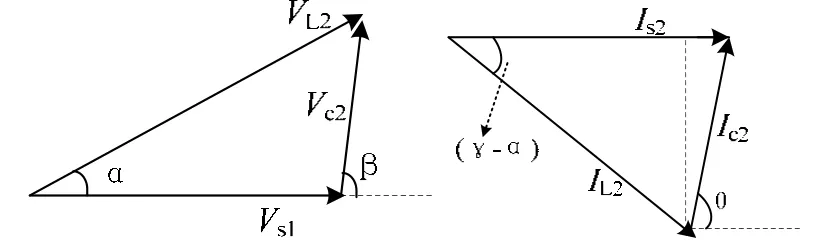
图4 电压补偿三角关系和电流补偿三角关系

根据图4的电压、电流补偿三角关系，可得：

UPQC的总视在功率、有功功率和无功功率为：

由式(8)～式(10)可知，在不同的补偿策略下，UPQC产生的无功功率恰好补偿负载所需的无功功率；串联侧消耗的有功功率由并联侧从电网吸收，整个UPQC并不消耗有功功率；随着串联侧补偿电压相角的变化，串联从不提供负载所需的无功功率到提供一定比例的无功功率，串、并联侧产生的总无功功率与负载所需的无功功率相等。

对最小电压补偿策略，DVR提供的电压与当前跌落后的电源电压相位一致，相角差β=0，相应地α=0；对最小能量补偿策略，DVR提供的电压与当前跌落后的电源电压相位相差90o，相角差β=π/2，相应地α=tan-1k；对完全补偿策略，α、β取决于电源电压跌落时的相角突变。通过上述关系和式(8)～式(10)不难得到不同补偿策略下UPQC的视在功率和串、并联部分的功率关系。

对式(8)求最小化可得：

对式(18)化简可得到：

由式 (12)可知，k=cosα是UPQC视在功率最小化的一个解，根据因式分解的必要条件可知，式 (12)的后一项乘积项无法做进一步的因式分解，难以得到具体的解析表达式。但注意到对实际的视在功率，在k和cosγ确定时，SUPQC存在唯一的最小值，因此可通过计算机数值计算确定近似解，进而得到对应k和cosγ的最优相角α，存储相应的二维数据表以便于实际使用。

对上述两个解，需要根据实际功率确定可行解，在MATBLAB中计算式(12)表示的UPQC视在功率并绘制cosα随k、cosγ变化的曲线，如图所示。

图5 UPQC最小化功率与k、cosγ的关系图

通过观察图5可看出，当k≥cosγ时，SUPQC最小的可行解为cosα=k；当k＜cosγ时，SUPQC最小的可行解由式（12）确定。由于负载电压相角α与补偿电压相角β存在式(5)的数学关系，为方便计算，若考虑电压跌落幅度（1-k）∈[0，0.5]，负载功率因数cosγ∈[0.5，1]，可建立最优相角α随k、cosγ变化的二维数据表。

3 仿真验证

在MATLAB中搭建三相三线UPQC的仿真模型，负载类型为三相阻感负载并联三相不控整流接电阻性负载。为便于直观对比，所有功率均以电源侧视在功率为基准标幺化。

图6 UPQC不同补偿策略下的仿真结果

图7 UPQC不同补偿策略下系统各部分的功率的对比

从图6、图7的对比可看出，最小电压补偿策略下，串联侧未补偿无功功率，负载的无功功率由并联侧补偿，整个UPQC的视在功率约为1.67(p.u.)；在最小能量补偿策略下，串联侧不仅补偿了电压，同时还对无功功率进行了补偿，但由于其提供了过多了的无功功率，导致并联部分须吸收额外的无功功率，整个UPQC的视在功率达到了1.93(p.u.)，并且大部分由DVR产生，这对于UPQC来说是非常大的功率等级，严重影响了UPQC的安全运行；最小视在功率补偿策略下，串联部分和并联侧共同补偿了负载所需的无功功率，而整个UPQC的视在功率也控制在1.38(p.u.)附近，并且串、并联部分的视在功率相差不大，相对于最小电压补偿策略和最小能量补偿策略来说，最小视在功率补偿策略显然更有利于UPQC的安全运行并能将开关器件的损耗降低到最小。

4 结论

在统一功率模型的基础上，分析了不同补偿策略下UPQC的功率关系，理论分析和仿真均表明：最小化视在功率补偿策略可有效降低串联部分和并联部分的视在功率，整个UPQC的功率等级和系统损耗得到有效降低，同时系统运行安全性得到了一定的提高。

[1] Akagi H．New trends in active filters for power conditioning[J]．IEEE Transactions on Industry Applications, 1996, 32(6)：1312-1322．

[2] 谭智力, 李勋, 陈坚, 等．基于简化p-q-r理论的统一电能质量调节器控制策略[J]．中国电机工程学报,2007, 27(36)：85-91．

[3] Mohammadi H, Varjani A, Mokhtari H．Multiconverter Unified power-quality conditioning system： MC-UPQC[J]．IEEE Transactions on Power Delivery, 2009, 24(3)：1679-1687．

[4] Forghani M, Afsharnia S． Online wavelet transform-based control strategy for UPQC control system[J]．IEEE Transactions on Power Delivery,2007, 22(1)：481-491．

[5] Yashomani K, Shyama D．Experimental investigation of a single-phase UPQC with minimum VA loading[J]．IEEE Transactions on Power Delivery,2007, 22(1)：373-380．

[6] Vinod K, Ambrish C．A New Control Philosophy for a unified power quality conditioner (UPQC) to coordinate load-reactive power demand between shunt and series inverters[J]．IEEE Transactions on Power Delivery, 2008, 23(4)：2522-2534．