List流上梯度Shrinking Solitons的广义Ricci张量

马冰清,潘全香（.河南师范大学数学与信息科学学院,河南新乡453007；.河南科技学院,河南新乡453003）

List流上梯度Shrinking Solitons的广义Ricci张量

马冰清1,潘全香2
（1.河南师范大学数学与信息科学学院,河南新乡453007；2.河南科技学院,河南新乡453003）

研究List流上梯度Shrinking Solitons的广义Ricci张量和广义数量曲率的增长行为.通过选取适当的截断函数,利用散度定理,得到了广义Ricci张量的积分上界估计.另外,还得到了广义数量曲率的积分上界估计.关键词：List流；梯度Shrinking Solitons；上界

由于俄罗斯数学家Perelman利用Ricci流的方法解决了Poincare猜想,使得Ricci流的研究已经成为一个非常热的研究方向.梯度RicciSolitons是Ricci的解,因此,研究梯度RicciSolitons的几何结构对理解Ricci的几何性质和Ricci流的奇性非常重要.Ivey证明了当流形是紧致的时候,Steady和Expanding的梯度RicciSolitons是平凡的[1].如果n=2或者n=3,则紧致的Shrinking的梯度RicciSolitons是平凡的.因此,自然的问题是：研究完备流形上梯度Solitons的几何结构.Cao研究了完备梯度Shrinking Solitons的位势函数的增长行为,证明了完备梯度Shrinking Solitons至多具有欧氏增长[2].Munteanu研究了完备流形上的Shrinking梯度RicciSolitons有关Ricci张量的积分上界估计,并且得到了数量曲率的积分上界估计[3].

为了建立与广义相对论之间的联系,List引入了List流[4],它是一种比Ricci流更加广泛的几何流,对于List流也有类似的梯度RicciSolitons的概念.本文研究了List流上的梯度Shrinking Solitons及其广义Ricci张量和广义数量曲率的增长行为,对研究List流的奇性有一定的理论意义.

1 梯度Solitons的概念及主要结果

其中Sij=Rij-（ 称Sij为广义Ricci张量）,α是正常数,则称（M,g）是对应于List流一个梯度RicciSolitons.特别的,ρ=0称为梯度Steady Solitons,ρ＞0为梯度Shrinking Solitons,ρ＜0为梯度Expanding Solitons.如果φ是常数,则式（1）变为了下面的Hamilton-Ricci流的梯度Solitons方程

因此,由式（1）定义的梯度Solitons是Hamilton-Ricci流的梯度Solitons的一个推广.令广义数量曲率S==R-α.则有下面的结果：

定理1设（M,g）是由式（1）定义的n维完备的梯度Shrinking Solitons.则对于任意的λ＞0,都有

另外,从定理1得到了广义Ricci曲率和广义数量曲率在指数体积元下的积分估计：推论1设（M,g）是由式（1）定义的n维完备的梯度Shrinking Solitons.则有

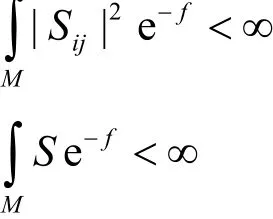
2 定理的证明

利用第二Bianchi恒等式和式（1）得到

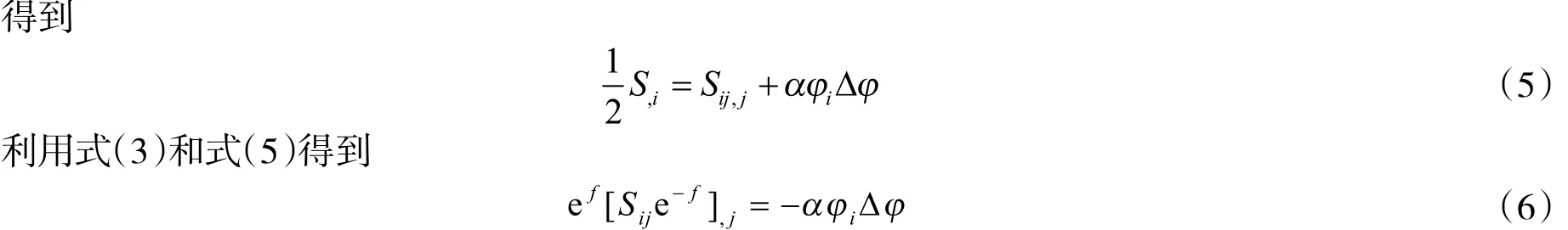
选取（M,g）上的一个截断函数φ,使得supφ⊂M,0≤φ≤1,|∇φ|≤C.则利用式（6）得到把式（8）式（9）带入式（7）得到

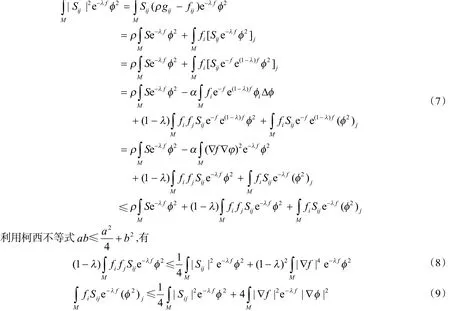
注意到,Yang-Shen[5]证明了：S≥0,并且存在一致的常数c使得

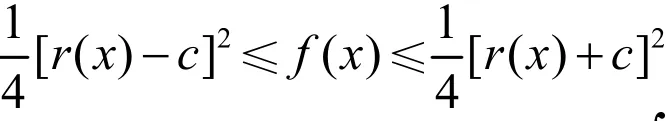
3 结论

本文研究了List流下的完备梯度Solitons广义Ricci张量和广义数量曲率的积分上界估计,完善了Solitons在完备流形上的结构.另外,作者在文献[6]中,分析了List流上的log熵函数,并计算了其关于时间t的第一变分公式.在文献[7]中探讨了紧致黎曼流形上的Yamabe Solitons的平凡结构.在文献[8]中,证明了List流上的微分Harnack不等式.结合本文,这些研究对梯度Solitons的发展将起到促进作用.

[1]Ivey T.Riccisolitons on compactthree-manifolds[J].Diff.Geom.Appl.,1993,3（4）：301-307.

[2]Cao H D,Zhou D.On Complete gradientshrinking Riccisolitons[J].J.DifferentialGeom,2010,85（2）：175-185.

[3]Munteanu O,Sesum N.On gradient Ricci solitons[J/OL].J.Geom.Anal.DOI：10.1007/s12220-011-9252-6.[2012-10-15]. http：//www.springerlink.com/content/y816mgn46l53n867.

[4]ListB.Evolution ofan extended Ricciflow system[J].Comm.Anal.Geom,2008,16（5）：1007-1048.

[5]Yang F,Shen J F.Volume growth for gradient shrinking solitons of Ricci-harmonic flow[J].Science China Mathematics,2012,55（6）：1221-1228.

[6]马冰清,潘全香.List流上的log熵函数[J].河南科技学院学报：自然科学版,2012,40（6）：44-47.

[7]马冰清,姚素霞.紧致黎曼流形上的Yamabe soliton[J].河南师范大学学报：自然科学版,2012,40（6）：12-13.

[8]Ma B Q.Differential Harnack estimate for a nonlinear parabolic equation under List's flow[J].Comm.Math.Appl.,2013,4（1）：75-83.

（责任编辑：卢奇）

Generalized Ricci tensor of gradient Shrinking Solitons under the List's flow

Ma Bingqing1,Pan Quanxiang2
（1.College ofMathematics and Information Science,Henan NormalUniversity,Xinxiang 453007,China；2.Henan Institute ofScience and Technology,Xinxiang 453003,China）

Growth estimates on the generalized Ricci tensor and the generalized scalar curvature of gradient shrinking solitons under the List's flow are studied in this paper．By choosing an appropriate cut-off function and the divergence theorem,upper bounds of the integral Ricci curvature are obtained．On the other hand,upper bound of the integral scalar curvature is obtained also．

List's flow；gradient Shrinking Solitons；upper bound

O186.12

A

1008-7516（2013）01-0059-03

10．3969/j．issn．1008-7516．2013．01．015

2012-12-05

国家自然科学基金（11171368）；河南省自然科学基金（092300410143）

马冰清（1978-）,女,河南商丘人,硕士,讲师．主要从事微分几何、概率论等方面的研究．