Sobolev空间等价模定理在偏微分方程中的应用
刘娟,原保全(.河南理工大学数学与信息科学学院,河南焦作454000;2.河南科技学院,河南新乡453003)
Sobolev空间等价模定理在偏微分方程中的应用
刘娟1,2,原保全1
(1.河南理工大学数学与信息科学学院,河南焦作454000;2.河南科技学院,河南新乡453003)
给出了Sobolev空间的等价模定理在偏微分方程理论中的应用,解决了一个Neumann边值问题弱解的存在性.
Sobolev空间;弱解;存在性;Neumann边值问题
在十九世纪末二十世纪初,数学这门学科有着飞速的发展,特别是Lebesgue积分理论和泛函分析的建立,使得人们能够在更广泛的空间使用更先进的理论来研究问题.在研究偏微分方程(PDE)解的存在性和唯一性问题时,人们发现,如果仅限于古典分析的范围内理解微商,并求偏微分方程的古典解,就会在使用近代的数学工具上受到限制,为了使泛函分析的方法能够应用于微分方程,就必须扩充微商的概念.Sobolev空间理论就是在上个世纪三十年代由俄国数学家Sobolev为了确定PDE解的存在性和唯一性以及研究函数空间中许多问题的需要而发展起来的,这些空间一般是由多个实变量的弱可微函数所组成的Banach空间[1-3].
本文在商空间的基础上,给出了Sobolev空间的等价模定理在PDE理论中的一个应用,解决了一个Neumann边值问题弱解的存在性问题.
1 预备知识
定义1设K是线性赋范空间,K0是K的闭线性子空间,将K中的向量分类,凡满足x1-x2∈K0,x1-x2∈Z的两个x1,x(2∈Z)归为同一类,称其为等价类[4].把一个等价类看作是一个新的向量,这种向量集合的全体构成的空间称为商空间,记为Wk+1,其元素[u]为

由于Pk(Ω)中的元素的k+1阶导数为0,故上式与代表元的选取无关,所以定义是有意义的,且显然有

2 等价模定理在偏微分方程中的应用
2.1 问题描述

的弱解.
关于问题(1)的弱解的存在性有如下定理:
定理设Ω⊂Rn是有界区域,∂Ω满足局部Lipschitz条件,f ∈L2(Ω),则问题(1)弱解的存在的充分必要条件是

证明:
必要性:
如果u∈H1(Ω)是问题(1)的弱解,则对于∀v∈ H1(Ω)有

令v为常值函数,则有
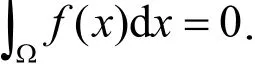
充分性:
考虑H1(Ω)中的子空间P0(Ω)(其实Wk+1,p(Ω)是所有的常值函数组成的子空间).根据等价模定理,商空间H1(Ω)P0(Ω)的范数可以取为

且在此范数下商空间H1(Ω)P0(Ω)是一个Banach空间.
易验证,此范数满足平行四边行法则,所以它可以诱导出内积,此内积为

在此内积下H1(Ω)P0(Ω)成为一个Hilbert空间.
我们定义泛函

最后一个不等式应用了等价范数定理.
于是T是H1(Ω)P0(Ω)上的有界线性泛函.由Riesz表示定理,存在

3 结论
对于偏微分方程的其他初边值弱解的存在性,利用Sobolev空间等价模定理类似于上面的讨论也可以相应的给出,Sobolev空间是泛函分析在偏微分应用中的桥梁,不仅对偏微分方程理论创新有重大的推动作用,在数值逼近等诸多分支中都有着重大的应用.
[1]Deny J,Lions-J L.Les espacese du type de Beppo Levi[M].Grenoble:Ann lnstFouries,1955:305-370.
[2]Yosida K.FunctionalAnalysis[M].New York:Springer-Verlag,1980.
[3]Adams R.Sobolev Space[M].New York:Academic Press,2003.
[4]张恭庆,林源渠.泛函分析讲义[M].北京:北京大学出版社,1987.
[5]马宝林,刘娟,吴亮.关于Sobolev空间的等价模定理的一个证明[J].河南科技学院学报:自然科学版,2010,38(4):95-97.
[6]胡春洪.加权Sobolev空间的完备性[J].数学杂志,2004,24(3):249-252.
[7]王万义,孙炯,郑志明.加权Sobolev空间中的Poincaré不等式[J].应用力学与数学,2006,27(1):112-118.
[8]陈恕行.一类Sobolev不等式及其应用[J].工程数学学报,1985,2(2):37-45.
(责任编辑:卢奇)
Application of the Sobolev space equivalent modulus theorem on partial differential equation
Liu Juan1,2,Yuan Baoquan1
(1.Henan Polytechnic University,Jiaozuo 454000,China;2.Henan Institute ofScience and Technology, Xinxiang 453003,China)
An application of the Sobolev space equivalent modulus theorem on the theory of partial differential equations,and solve the existence of weak solution of a Neumann's problem.
Sobolev space;weak solution;existence;Neumann's problem

O186.12
A
1008-7516(2013)01-0056-03
10.3969/j.issn.1008-7516.2013.01.014
2012-12-11
国家自然科学基金(10771052)
刘娟(1979-),女,回族,宁夏石嘴山人,讲师,硕士在读.主要从事偏微分方程研究.
原保全(1965-),男,博士,教授.主要从事微分方程和数学流体力学偏微分方程研究.

