城市机动交通与非机动交通的演化博弈分析

郭运瑞,董瑞

（河南科技学院,河南新乡453003）

城市机动交通与非机动交通的演化博弈分析

郭运瑞,董瑞

（河南科技学院,河南新乡453003）

利用演化博弈中的动态复制方法,以城市内城区的机动交通群与非机动交通群为研究对象,对机动交通与非机动交通随机配对后,根据鹰鸽博弈的思想建立了博弈双方的收益矩阵.讨论了交通执法频率、范围和力度等模型参数,易发生交通拥堵路段的机动交通与非机动交通违规选择的影响,解释了城市交通拥堵的部分原因：出行者的个人素质因素和地方政府交通执法因素.

演化博弈；复制动态；交通拥堵；稳定性

我国的交通拥堵问题首先出现在特大城市,很快省会城市、计划单列市也卷入交通拥堵之中,甚至一些三线城市都相继出现了严重的交通拥堵状况.交通拥堵对经济发展和居民生活产生了很多负面影响：增加了城市的建设费用、降低了基础设施的使用寿命,增加了居民的出行时间、出行费用等成本,降低了居民的生活质量,交通事故频发、交通事故隐患严重,城市大范围、长时间的交通拥堵,严重阻碍城市经济社会的健康发展[1].造成城市交通拥挤的原因很多,我国城市化速度快、私家车辆剧增,而道路的设施运输能力和交通管理措施没有及时地配套跟进,城市交通信号控制不能发挥作用等都是形成和加剧拥堵的原因.大城市以功能分区进行规划,增大了市民的出行需要,加重了市民对私人汽车的依赖,同时也加重了城市公共交通负担.还有一些城市商业区域过于集中于市中心,各种服务、商品集中在一条街上,人流量非常大,但却没有提供足够的停车位,机动车道、人行道的空间严重不足[2-4].

大中型城市普遍存在的行人、非机动车和机动车三元混合交通流结构,使得现有道路交通设施的运输能力得不到充分利用.交通管理只是在路口进行,而中间路段是机动车和行人混行,流量大、管理乱,从而造成在特定地区和特定时段的交通瘫痪.本文应用演化博弈理论的思想和方法,把出行人群是否遵守交通规则当作一个学习的渐进演化系统,强调博弈的动态性和宏观性,并注重从分析影响系统演化过程及演化稳定的出行人素质及交通法规执行等因素的角度,对出行人群中机动车司机与非机动车及行人的策略进行研究.

1 演化博弈模型

演化博弈论是把博弈论和生物演化过程分析结合起来的一种新理论,它起源于行为生态学和生物进化论[5-6].演化博弈论研究的对象是一个“种群”,而不是单个的参与者.演化博弈思想用于分析交通拥堵问题的文献比较少,文献[7]建立了单总体出行方式演化博弈模型.由于出行者的有限理性,其最佳策略就是模仿和改进过去自己和别人的最有利战略.通过长期的模仿和改进,所有的博弈方会趋于某个稳定的策略,这个稳定的策略被称为“演化稳定策略”（evolutionary stable strategy,ESS）[6].当出行者绝大多数选择某种策略（遵守交规或者不遵守）时,少数人违背这种策略对自己不利.在大群体反复博弈中,复制动态（replication dynamics）演化博弈是常用的一种.复制动态是描述某一特定策略在一个种群中被采用的比例或频率的动态微分方程,其动态变化速度可以用动态微分方程表示,式中x为一个种群中博弈方采用策略S的比[6].

2 本文符号

为了研究方便,本文引入符号如下：

x：内城区行驶的机动车辆选择遵守交通规则的概率；

y：内城区行驶的非机动车辆和行人选择遵守交通规则的概率；

u1,u2：分别表示机动车和非机动车遵守交规时通行某路段的支付；

v1：机动交通遵守交规,非机动交通不遵守时节省的等待支付；

v2：非机动交通遵守交规,机动交通不遵守时节省的等待支付；

p1：机动交通遵守交规,非机动交通不遵守时发生交通事故的概率；

p2：非机动交通遵守交规,机动交通不遵守时发生交通事故的概率；

p3：两者均不遵守交规时发生交通事故的概率；

q1：机动交通不遵守交规被处罚的概率；

q2：非机动交通不遵守交规被处罚的概率；

g1：机动交通不遵守交规由处罚引发的支付；

g2：非机动交通不遵守交规由处罚引发的支付；

f1,f2：分别表示机动交通遵守交规,非机动交通不遵守时由交通事故引发的两者的支付；f3,f4：分别表示机动交通不遵守交规,非机动交通遵守时由交通事故引发的两者的支付；f5,f6：分别表示二者均不遵守时由交通事故引发的两者的支付；

3 演化博弈分析

3.1 博弈主体

以机动交通方式出行者与以非机动交通方式出行者作为城市内城区某些路段（路口与非路口）交通拥堵形成与发展的两大因素,二者的行为发展遵循着演化博弈论的基本假设.

3.2 策略选择

双方的策略集合分别为C（遵守交规,不遵守交规）和L（遵守交规,不遵守交规）.当两者都选择遵守交规时,就会选择耐心等待,交通拥堵状况就会缓解甚至不会发生拥堵；当机动交通选择遵守交规时而非机动交通选择不遵守时,可以减少自己的等待时间,但同时增加了发生事故的风险；当交通拥堵严重、等待时间过长时,非机动交通也有不遵守交规的动力；当两者都选择不遵守交规时,拥堵状况严重.这种发展系统是通过自身的演化所形成的,机动交通和非机动交通根据对方的策略选择,考虑在自身群体中的相对适应性来选择和调整各自的策略.

3.3 收益矩阵

根据鹰鸽博弈[5]的思想建立机动交通与非机动交通博弈的收益矩阵如表1所示：

表1 机动交通与非机动交通博弈的支付矩阵Tab.1 PayingMatrix ofevolutionary game ofmotorized and non-motorized transport

3.4 机动交通与非机动交通演化博弈支付分析

3.4.1 机动交通的支付分析当机动交通选择遵守交规时,其支付为

当机动交通选择不遵守交规时,其支付为

因此,机动交通的平均支付为

由此可得到机动交通选择遵守交规的复制动态方程为

3.4.2非机动交通的支付分析同机动交通的支付分析过程类似,同样可以得到非机动交通选择联动发展时的复制动态方程为

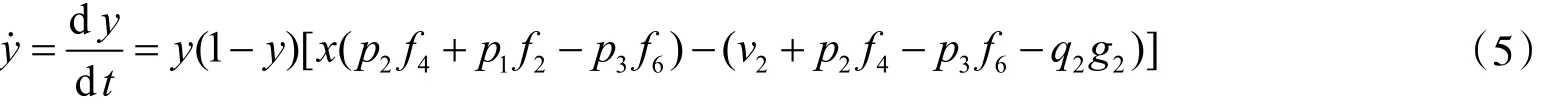
3.5 机动交通与非机动交通演化博弈稳定性分析

（1）在平衡点E1（0,0）,系统在平衡点E1（0,0）的稳定情况有如下3种：①当机动交通与非机动交通均可以由交通违章获得便利（v1＞0,v2＞0）,减少支付,因违章被交管部门惩罚而增加的支付（q1g1,q2g2）非常少,是否交通违规对由交通事故引发的支付影响不大时, P2＞0,Q2＞0时,由于det J＞0,trJ＜0,平衡点E1（0,0）是系统的稳定点；②当全路段检查交通违规,机动交通与非机动交通都会因违规被查而带来较大的支付时,P2＜0,Q2＜0,由于det J＞0,trJ＞0平衡点E1（0,0）是系统的不稳定平衡点；③当全路段检查交通违规,机动交通会因违规被查而带来较大的支付而非机动交通不会因违规而增加支付时,P2Q2＜0,由于det J＜0,平衡点E1（0,0）是系统的鞍点.

（2）在平衡点E2（0,1）,系统在平衡点E2（0,1）的稳定情况有如下3种：①当机动交通可以由交通违章获得便利（v1＞0）,减少支付,因违章被交管部门惩罚而增加的支付（q1g1）非常少,而非机动交通因违章被交管部门惩罚而增加的支付（q2g2）比较大时,P1-P2＜0,Q2＜0,由于det J＞0,trJ＜0,平衡点E2（0,1）是系统的稳定点,但这种情况实际上几乎不会发生；②当发生与①相反的情况时,P1-P2＞0,Q2＞0,由于det J＞0,trJ＞0,平衡点E2（0,1）是系统的不稳定平衡点；③当全路段检查交通违规,机动交通与非机动交通都会因违规被查而带来较大的支付或者全路段均不检查交通违规时,（P1-P2）Q2＜0,由于det J＞0,平衡点是系统的鞍点.

（4）在平衡点E4（1,1）,系统在平衡点E4（1,1）的稳定情况有如下3种：①当全路段检查交通违规,机动交通与非机动交通都会因违规被查而带来较大的支付时,（P1-P2）＜0,（Q1-Q2）＜0,由于,平衡点E4（1,1）是系统的稳定点；②当机动交通与非机动交通均可以由交通违章获得便利,因违章被交管部门惩罚而增加的支付非常少发生与①相反的情况时,（P1-P2）＞0,（Q1-Q2）＞0,由于平衡点E4（1,1）是系统的不稳定平衡点；③当全路段检查交通违规,机动交通与非机动交通只有一方会因违规被查而带来较大的支付时（,Q1-Q2）（P1-P2）＜0,由于detJ＜ 0,平衡点E（41,1）是系统的鞍点.

trJ=0,下面对P2Q（2P1-P2）（Q1-Q2）P1Q1的符号进行分析.当博弈方生在交通非常拥挤的路段,机动交通与非机动交通同时选择违规与单方违规相比只是加重了拥挤的程度,并不增加双方由交通事故引发的支付时,可假定P1＞0,Q1＞0.当全段交通违规检查,机动交通与非机动交通都会由于违规招致的惩罚支付远大于违规产生的便利时（,P1-P2）＞0（,Q1-Q2）＞0,P2＜0,Q2＜0,因此detJ＜ 0；当机动交通与非机动交通均可以由交通违章获得便利,而因违章被交管部门惩罚而增加的支付非常少时（,P1-P2）＞0（,Q1-Q2）＞0, P2＞0,Q2＞0,因此detJ＜ 0；当全路段检查交通违规,机动交通与非机动交通只有一方会因违规被查而带来较大的支付时（,Q1-Q2）（P1-P2）＜0,P2Q2＜0,detJ＜ 0.综上,detJ＜ 0恒成立.

4 结论与建议

本文根据鹰鸽博弈的思想建立了机动交通与非机动交通博弈的收益矩阵,得到5个平衡点E1（0,0）,E2（0,1）,E3（1,0）,E4（1,1）和进一步分析发现各平衡点仅在特定情况下才能成为稳定点：当机动交通与非机动交通均可以由交通违章获得便利,减少支付,因违章被交管部门惩罚而增加的支付非常少,是否交通违规对由交通事故引发的支付影响不大时,平衡点E1（0,0）是系统的稳定点；当机动交通可以由交通违章获得便利,减少支付,因违章被交管部门惩罚而增加的支付非常少,而非机动交通因违章被交管部门惩罚而增加的支付比较大时,平衡点E2（0,1）是系统的稳定点,但这种情况实际上几乎不会发生；当非机动交通可以由交通违章获得便利,减少支付,因违章被交管部门惩罚而增加的支付非常少,而机动交通因违章被交管部门惩罚而增加的支付比较大时,平衡点E3（1,0）是系统的稳定点；当全路段检查交通违规,机动交通与非机动交通都会因违规被查而带来较大的支付时,平衡点E4（1,1）是系统的稳定点；而平衡点不会成为稳定点.可见仅在当全路段检查交通违规,机动交通与非机动交通都会因违规被查而带来较大的支付时,模型的演化稳定策略是（遵守交规,遵守交规）.即要想减少因机动交通与非机动交通不守交规而引起的交通拥堵,严格检查交通违规并严厉处罚才能实现双方的守法.

文中模型只考虑了严格执法给机动交通与非机动交通带来的惩罚性支付,并未涉及交通执法成本和当事人守法意识等问题,模型不能很好地作为对现实交通情景的准确抽象.应该认识到除了复制动态,演化博弈还有更加先进的学习机制,比如强化学习、适应性学习的机制,今后需对它们做进一步的应用研究.

[1]刘波.缓解城市交通拥堵探讨[J].公共管理,2011（6）：145-147.

[2]闫庆军.基于外部性的交通拥堵成因分析与缓解策略[J].经济论坛,2005（5）：57-59.

[3]赵冬斌,刘德荣,易建强.基于自适应动态规划的城市交通信号优化控制方法综述[J].自动化学报,2009,35（6）：676-681.

[4]张莉娜.浅谈解决中国城市交通拥堵问题的主要思路[J].现代企业文化,2009（5）：118-119.

[5]Maynard SJ.The theory ofgamesand theevolution ofanimalconflicts[J].Journalof TheoreticalBiology,1974,47（1）：209-221.

[6]Maynard SJ,PriceGR.The logic ofanimalconflict[J].Nature,1973,246：15-18.

[7]陈星光,周晶,朱振涛.城市交通出行方式选择的演化博弈分析[J].管理工程学报,2009,23（2）：140-142.

[8]Friedman D.Evolutionary games in economics[J].Econometrica,1991,59（3）：637-666.

（责任编辑：卢奇）

Evolutionary game ofmotorized and non-motorized transport in city

Guo Yunrui,Dong Rui
（Henan InstituteofScienceand Technology,Xinxiang453003,China）

By using of the evolutionary game theory based on bounded rationality,proposes a dynamic unsymmetrical replicating model of motorized and non-motorized transport．Motorized and non-motorized transport are random ly paired based on the idea of hawk-dove game payoffmatrix of the game．This paper discusses the impact of themodel parameters：the traffic enforcement frequency,scope and intensity of the city．The reasons of urban traffic congestion have been explained：the traveler's personal quality factors and local government traffic enforcement factors．

evolution；game theory；traffic congestion；stability

O225

A

1008-7516（2013）03-0090-05

10．3969/j．issn．1008-7516．2013．03．019

2013-04-18

2012年河南省政府决策研究招标课题（2012B252）

郭运瑞（1964-）,女,河南辉县人,教授．主要从事最优化理论及应用、小波分析及应用研究．