多电极电磁流量计用于非轴对称流的测量

赵宇洋，张 涛，Lucas G

多电极电磁流量计用于非轴对称流的测量

赵宇洋1，张 涛1，Lucas G2

(1. 天津大学天津市过程检测与控制重点实验室，天津 300072；2. 英国哈德斯菲尔德大学，哈德斯菲尔德 HD1 3DH，英国)

为解决两电极电磁流量计对于速度非轴对称分布的敏感问题，基于Shercliff权函数提出区域权函数概念，研究其计算方法并设计出多电极电磁流量计．通过多电极传感器测量不同位置的弦端电压，计算管道截面各区域的局部轴向平均速度，并实现体积流量的测量．介绍了多电极电磁流量计传感器设计，通过测量偏流发生器下游的非轴对称单相流及倾斜管固-液两相流，证明该设计对于非轴对称流具有较高的流量测量精度及可靠的速度分布测量结果．

区域权函数；电磁流量计；非轴对称流

多电极电磁流量计(multielectrode electromagnetic flow meter，MEFM)针对非轴对称流测量应运而生，通过获得流动截面处不同位置的感应电势差，利用任意流型下的平均流速表达式，实现速度分布和体积流量测量，以解决两电极电磁流量计的弊端．Horner等[1]提出以层析成像为基础的6电极电磁流量计测量平均流速，并通过实验证明多电极流量计对速度分布不敏感，但未给出局部速度信息. Teshima等[2]设计出旋转磁场下的多电极电磁流量计．徐立军等[3]对多电极阵列的数量与几何尺寸进行了研究．

自Shercliff[4]给出两电极电磁流量计权函数表达式以来，很多学者都致力于权函数理论的发展．Lim等[5]通过有限元容积法仿真比较了4种不同栅格划分方法对不同流型的测量效果．Lucas等[6]针对多电极权函数的仿真求取方法进行了详细研究．张小章[7]利用解析法对权函数计算进行探索．

此外，学者们还希望利用电磁测量原理解决多相流领域的难题．Bernier等[8]将多电极测量方法应用于两相流测量当中，Gladden等[9]也曾做过有益的尝试．

本文中基于Shercliff权函数理论发展出区域权函数的概念，并基于该理论设计多电极电磁流量计测量系统，以仿真数据为基础优化样机模型[9]，通过测量局部轴向平均速度，解决非轴对称的单相流及固-液两相流测量问题．

1 区域权函数及多电极电磁流量计

在Shercliff权函数理论[10]指出，流动截面上各个流体质点都影响感应电动势的数值，并解析得到长筒型两电极流量计的权函数二维近似计算公式，指出由于权函数分布不均匀导致两电极电磁流量计对流速分布轴对称比较敏感．

多电极测量中，J对电极布置在管道内圆周上(见图1)，每对电极都沿平行于直径的弦分布．假设测量截面处包含总数为K，且K→∞的尺寸极小的流体质点，并且所有质点中直径的最大值趋于零，则各电极间的感应电动势可以表示为极限求和的形式，即

式中：Uj为第j对电极测量的感应电压；K为测量截面所包含的质点个数；vk为第k个质点的轴向速度；Wk,j为第k个质点对第j个感应电压的权函数；Ak为该质点的面积；B为测量截面处的磁感应强度；a为管道半径．

图1 测量截面区域划分方式Fig.1 Layout of region in cross section

本文中提出的区域权函数不再以单独的流体质点作为研究对象，而是将流动截面划分为I个区域．假设第i个区域内包含的流体质点个数为in，且满足，则in个质点的轴向速度求和便得到该．管道截面上每一区区域的轴向平均速度域内流体的流速vi切割磁力线所产生的感应电动势对任意对电极的感应电压Uj都有贡献，贡献的大小通过区域权函数wij反映．区域权函数理论揭示了感应电压与区域内流速的关系，进而由流动截面处的速度分布信息得到体积流量值，解决了两电极测量中速度分布非轴对称对于流量测量的影响．

如图1所示，文中多电极电磁流量计采用16个电极均匀分布在管道内壁，GNDe和GNDe′为接地电极，电极对e1e1′～e7e7′分布在与直径平行的弦上．测量截面采用如图1所示方式划分为7个区域，每对电极对应1个区域．采用该种划分方式的依据为：①平行布置各区域更有利于反映管道内速度剖面的变化；②仿真表明，电极位于各区域在y方向上的中心处时，可以获得最强的感应电动势信号，提高计算和测量精度．

多电极流量计不同电极对间的感应电压是各区域内轴向平均速度共同作用的结果，即

式中Ai为各区域面积值．权函数wij的大小表示了不同区域的流体对各感应电压值的贡献大小．

利用COMSOL Multiphysics软件建立三维仿真模型，在电极所在二维测量平面处求取区域权函数wij．因此，多电极电磁流量计测量方程可表示为

式中：V为包含I个区域轴向平均速度的速度矩阵；U为包含J个感应电压测量值的电压矩阵；W为IJ×维的区域权函数矩阵；A为II×维以I个区域的面积为对角元素的对角阵．

如式(4)所示，多电极传感器测量不同位置的弦端电压，计算得到图1中各区域内的轴向平均速度．对比两电极电磁流量计，仅由布置在直径处的电极测量得到电压，并以此计算整个截面处的平均速度而言，利用区域权函数原理的多电极电磁流量计提供测量截面处速度分布的详细信息，解决了速度分布非轴对称的敏感问题．

本文中阐述的多电极电磁流量计传感器设计如图2所示．聚甲醛树脂材料制成测量管组件，两端以法兰连接．16个非导磁316,L不锈钢电极阵列以22.5°圆心角均匀布置在测量管中部，耐腐蚀性好且不会对工作磁场造成干扰．励磁系统采用Helmholtz线圈，由图2中所示的夹具精确定位，以保证电极阵列所在的测量截面处磁感应强度均匀分布．信号导线槽用来固定工作磁场内电极间以及电路中的所有导线，使其都平行于磁场方向，避免非流动因素产生的干扰电压．

图2 多电极电磁流量计传感器Fig.2 Transducer of MEFM sensor

2 单相非轴对称流实验

2.1 实验系统简介

实验在英国Huddersfield大学低压固水两相流装置上进行，如图3所示．

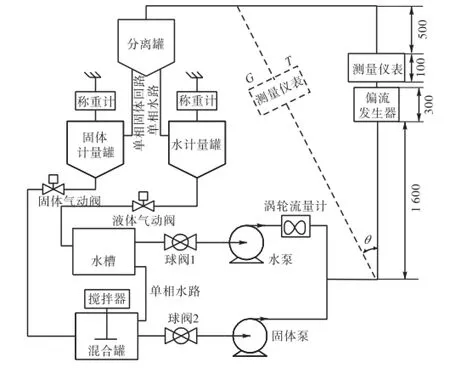
图3 实验装置示意Fig.3 Layout of experimental setup

装置分为介质源、计量管段、可调角度的实验管段及计算机控制系统4部分；管道内径80,mm，实验管段长度2.5,m；实验的液相介质为水，流量范围为0.7～17.6,m3/h；涡轮流量计经称重装置校正后提供单相水实验中体积流量的标准值，计量精度为±0.5%.

单相非轴对称流实验中，关闭球阀2，将如图4所示偏流发生器串入实验管段，多电极电磁流量计安装在其下游出口处(见图3)．偏流发生器利用不同直径的圆形流量通道得到非轴对称分布的单相流，电磁流量计不仅可以实现对单相流在管道截面处速度分布的在线测量，也可通过流量计转换器中的微处理器计算得到流体的体积流量．

图4 偏流发生器结构Fig.4 Structure of flow conditioner

管道截面的速度分布标准值由皮托管获取，通过测量流体总压和静压确定流速．皮托管安装在电磁流量计电极所在平面，调整位置沿16个径向方向进行测量，在整个截面上获得80个不同坐标点处的速度值，计算第i个区域中所包含测量点的数值平均，即得到该区域内的轴向平均速度标准值ˆiv．由于皮托管自身几何尺寸，移至管壁附近占据一定体积，因此在面积较小的区域1和区域7内只包含一个测量点.

2.2 单相流实验结果分析

多电极电磁流量计对单相非轴对称流的实验在6种不同流量下进行，各区域速度分布测量结果与皮托管标准值的对比如图5所示．皮托管作为侵入式测量方法，会对流体流动引入干扰，但在目前有限的技术条件下，仍可作为局部轴向平均速度分布的标准值来衡量流量计的性能．

图5表明，在不同流量条件下，多电极电磁流量计测量的管道截面速度分布呈现由偏流发生器结构所致的流动规律．特别是在区域2～5处，皮托管测量点相对密集，标准值精度较高，多电极电磁流量计对于轴向平均速度的测量一致性较好．虽然速度值在区域1和区域7处出现最大误差，但原因之一是由于皮托管侵入式测量原理的限制，以及在区域1和7内只有1个测量点，造成这2个区域内速度标准值精度较低；另外，由Shercliff理论可知[4]，与电极距离越近权函数数值越高，因此区域权函数11w和77w的数值远高于其他，所以感应电压值1U和7U在测量中的微小扰动也会带来该区域内轴向平均速度的较大差异．

在图5所示单相流实验中，多电极电磁流量计对体积流量的测量结果与涡轮流量计标准值的相对误差如表1所示．

表1中体积流量的标准值由涡轮标准表提供，测量值由多电极电磁流量计输出．电磁流量计转换器在处理数据时，按照式(4)直接计算得到速度分布结果，没有经过任何系数校正．表1显示电磁流量计对体积流量测量的相对误差在1.0%±范围内，具备较高测量精度．

图5 MEFM与皮托管速度分布测量结果比较Fig.5 Results comparisons of velocity profile between MEFM and Pitot

3 固-液两相流实验

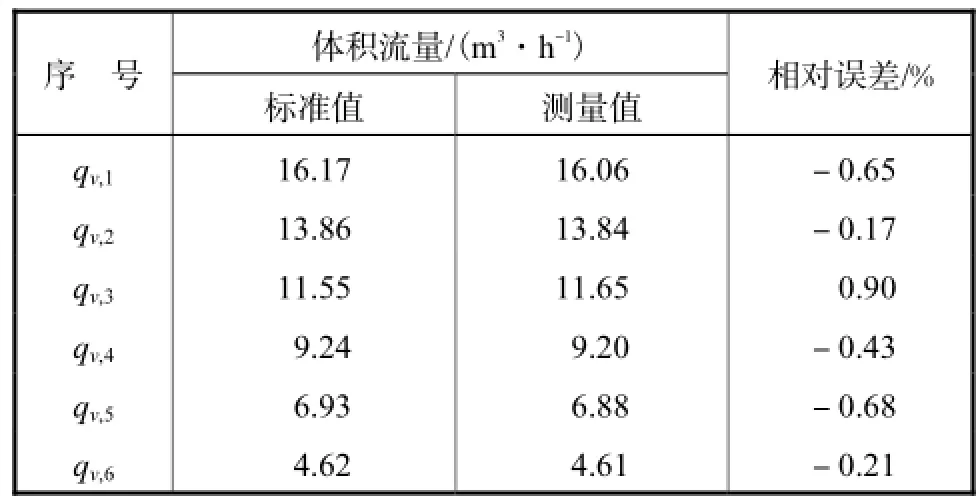
表1 单相非轴对称体积流量测量相对误差Tab.1 Relative errors of non-axisymmetric flow rate

3.1 两相流实验系统简介

如图3所示，固-液两相流实验在30°倾斜管中进行，固相介质为非电导性球形颗粒，平均直径5,mm、材料平均密度为1,340.8,kg/m3．小颗粒与水在混合罐中均匀混合，通过调整球阀1、2的开度控制液相流量wq和固相流量sq，体积流量的标准值w,stq和s,stq由称重系统测量；管道内局部固相含率s,iα由6电极探针测量[11]，测量点选取和标准值计算与皮托管所用方法一致；多电极电磁流量计测得固-液两相流中水的体积流量为

式中s,iα为第i个区域内固体的相含率．在实际应用中还可采用电阻层析成像技术等来测量局部固相含率s,iα的值．

3.2 两相流实验结果分析

针对深海采矿业中的矿石传输问题设计了倾斜管实验．采矿现场通常利用液压升降系统将矿石与海水两相混合物由倾斜管道运送至船上，角度在30°左右．开采中需要实时监测矿石流速，不仅为获得矿石的质量流量信息，更为了避免传送速度过低而造成矿石循环流动甚至回流至海床的现象．

在两相流实验中，多电极电磁流量计安装在30°倾斜管段中，区域1位于管道上侧(图3中“T”侧)，区域7位于下侧(图3中“G”侧)．利用高速照相机拍摄透明有机玻璃管内的流动情况，照片表明倾斜管道下侧的流体速度低于上侧并且会产生回流．

如图6所示，利用带箭头的圆圈分别标注位于管道上、下侧的颗粒组A、B，箭头方向指示颗粒运动方向．通过对比图6(a)和(b)，表明位于管道上侧的A组颗粒运动速度明显高于下侧的B组，并且B组颗粒呈现逆向流动．

对于固-液两相流，多电极电磁流量计可以实现对导电相在截面处的速度分布和体积流量测量．本文中两相流实验在6种不同固相含率条件下进行，通过调节球阀1、2开度得到不同相含率的两相流，利用差压变送器计算上下游压差得到管道内平均固相含率αs,DP．

图7为30°倾斜管实验中水相速度分布的测量结果，fm1～fm6表示6种实验条件(固相含率值见表2)，每个点表示管道截面各区域内的轴向平均速度．

图6 30°倾斜管固-液两相流动图像Fig.6 Flow pictures of 30°inclined pipe

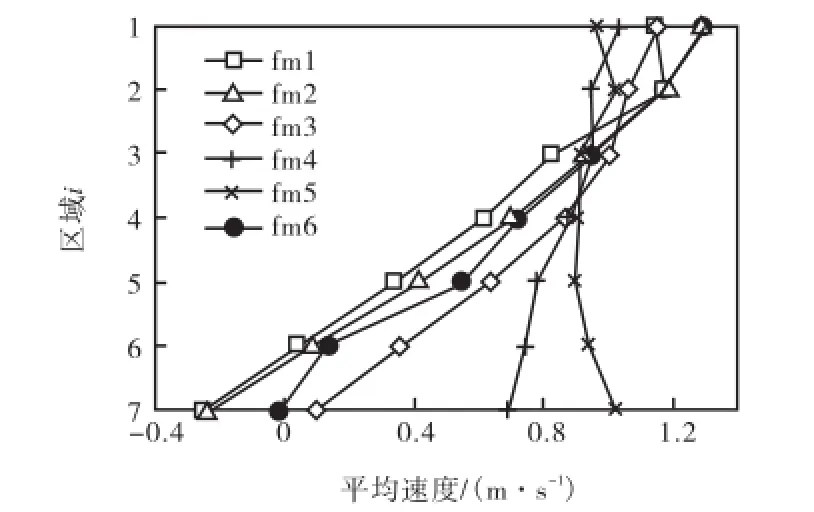
图7 30°倾斜管水相速度分布测量结果Fig.7 Water velocity profile in soil-water two-phase flow of 30°inclined pipe

如图7所示，利用多电极电磁流量计在6种实验条件下测量管道截面速度分布的结果表明：在大多数流动情况下，管道上侧的速度值高于下侧，并且局部轴向速度分布的规律与Lucas[13]研究结果一致．在固相含率较高的fm1和fm2测量条件下，管道下侧区域内的速度为负值，表明该区域内流体出现逆向回流，与高速相机采得的图片一致．

在图6所示两相流实验中，多电极电磁流量计对水相体积流量的测量值与称重装置标准值的相对误差如表2所示．误差计算为

由式(5)可知，局部固相含率s,iα的精度也影响电磁流量计的流量测量，由于6电极探针测量精度的限制，使得电磁流量计对水相体积流量测量的误差波动性较严重．

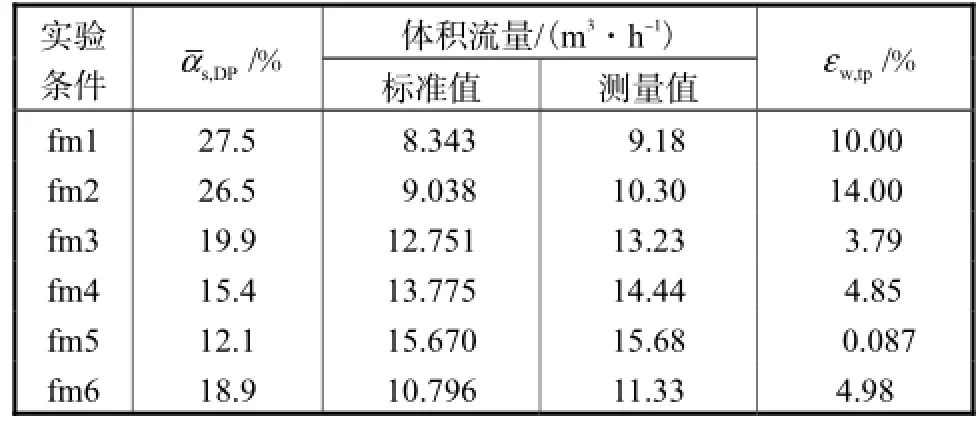
表2 固-液两相流倾斜管水相体积流量相对误差Tab.2 Water flow rate relative errors of inclined solid-water two-phase flow

4 结 语

由Shercliff权函数提出区域权函数理论，将管道截面划分为若干区域，既得到局部轴向平均速度信息，又实现对体积流量的测量，消除了速度分布非轴对称的影响．文中设计了多电极电磁流量计，并进行了单相及两相流实验．通过测量偏流发生器下游的单相流，表明对于弯头、阀门下游或者管径突变等造成的单相非轴对称流，都可以使用多电极电磁流量计．固-液两相流实验结果表明，该流量计可以提供管道测量截面的局部轴向速度信息，如果结合高精度的固相含率测量手段，必将提高多电极电磁流量计的测量精度．

［1］ Horner B，Mesch F，Trächtler A. A multi-sensor induction flowmeter reducing errors due to non-axisymmetric flow profiles[J]. Measurement Science and Technology，1996，7(3)：354-360.

［2］ Teshima T，Honda S，Tomita Y. Electromagnetic flowmeter with multiple poles and electrodes[C] // Instrumentation and Measurement Technology Conference. Hamamatsu，Japan，1994：1221-1224.

［3］ 徐立军，王 亚，乔旭彤，等. 多对电极电磁流量计传感器电极阵列设计[J]. 仪器仪表学报，2003，24(4)：335-339.

Xu Lijun，Wang Ya，Qiao Xutong，et al. Design of electrode array of multi-electrode electromagnetic flowmeter[J]. Chinese Journal of Scientific Instrument，2003，24(4)：335-339(in Chinese).

［4］ Shercliff J A. The Theory of Electromagnetic Flow-Measurement[M]. New Ed. Cambridge，UK：Cambridge University Press，1987.

［5］ Lim K W，Chung M K. Numerical investigation on the installation effects of electromagnetic flowmeter next term downstream of a 90° elbow-laminar flow case [J]. Flow Measurement and Instrumentation，1999，10：167-174.

［6］ Lucas G P，Leeungculsatien T. A new method of measuring velocity profiles using a multi-electrode electromagnetic flow meter [C] // 6th World Congress on Industrial Process Tomography. Beijing，China，2010：1016-1025.

［7］ 张小章. 基于流动电磁测量理论的流场重建[J]. 计量学报，1998，19(2)：79-89.

Zhang Xiaozhang. Flow field reconstruction based on electromagnetic measurement theory[J]. Acta Metrologica Sinica，1998，19(2)：79-89(in Chinese).

［8］ Bernier R N，Brennen C E. Use of the electromagnetic flowmeter in a two-phase flow[J]. International Journal of Multiphase Flow，1983，9(3)：251-257.

［9］ 朴立华，张 涛，王军鹏，马艳芳．基于CFD的双锥形孔板浮子流量计的优化[J]. 天津大学学报，2012，45(3)：236-24．

Piao Lihua，Zhang Tao，Wang Junpeng，et al． Optimization of double-cone orifice rotameter based on CFD[J]. Journal of Tianjin University：Science and Technology，2012，45(3)：236-241(in Chinese)．

［10］ Sankey M，Yang Z，Gladden L，et al. Sprite MRI of bubbly flow in a horizontal pipe[J]. Journal of Magnetic Resonance，2009，199(2)：126-135.

［11］ Al-hinal S，Lucas G. Non-invasive velocity and volume fraction profile measurement in multiphase flows[J]. Journal of the Japanese Society for Experimental Mechanics，2009，9：s7-s12.

［12］ Lucas G. Gas volume fraction and velocity profiles：Vertical and inclined bubbly air-water flows[J]. Journal of Visualisation，2006，9(4)：419-426.

Measuring Non-Axisymmetric Flow by Multielectrode Electromagnetic Flow Meter

Zhao Yuyang1，Zhang Tao1，Lucas G2
(1. Tinanjin Key Laboratory of Process Measurement and Control，Tianjin University，Tianjin 300072，China；2. University of Huddersfield，Huddersfield HD1 3DH，UK)

A multi-electrode electromagnetic flow meter(MEFM)based on region weight function，which is derived from Shercliff weight function theory，has been developed and presented in this paper. The novel flow meter uses the region weigh function theory to reconstruct the local mean velocities of measurement cross-section and flow rate by acquiring the induced voltages at the boundary along flow pipe circumference and images the velocity profile in real time. This paper describes the design of MEFM. The experiments on non-axisymmetric single conductive flow which is generated by a flow conditioner and soil-water flow have been undertaken and the results are presented in order to demonstrate that the novel multi-electrode electromagnetic flow meter is highly suited in measuring volumetric flow rate and mapping the local average velocity of non-axisymmetric flow.

region weight function；electromagnetic flow meter；non-axisymmetric flow

TP216.1

A

0493-2137(2013)06-0559-06

DOI 10.11784/tdxb20130615

2012-04-24；

2012-06-25.

国家自然科学基金青年科学基金资助项目(61101227).

赵宇洋（1982— ），女，博士研究生，rainsunyy@126.com.

张 涛，zt50@tju.edu.cn.