一种渐晕纹理图像自动分类方法

何 凯，张伟伟，孔祥文

一种渐晕纹理图像自动分类方法

何 凯，张伟伟，孔祥文

(天津大学电子信息工程学院，天津 300072)

传统纹理分类方法对光照比较敏感，不均匀的光照分布(如渐晕)会在很大程度上影响纹理分类的准确率．为解决此类问题，针对渐晕纹理图像，提出了一种纹理图像自动分类方法；在利用小波包提取纹理指数算法的基础上，根据渐晕系数自动调整各小波包分解系数，从而消除了渐晕现象对纹理特征指数的影响，最终提高了纹理分类的准确率．仿真实验结果表明，利用此方法对渐晕纹理图像进行分类，准确率有了较大程度的提高，取得了比较理想的分类效果．

纹理分类；特征指数提取；渐晕模型；小波包变换；支持向量机

作为图像处理领域的重要研究内容，纹理图像分析在计算机视觉和模式识别领域具有重要意义，在遥感、目标识别、图像检索、医学图像分析和智能机器人导航等领域具有重要的研究价值[1-2]．目前，纹理图像分析主要集中在纹理特征提取和纹理分类2个方面．其中，纹理特征提取是进行纹理描述、分类与分割的关键环节，直接影响纹理分类的准确率，受到了人们的普遍关注．

目前，纹理特征提取方法主要分为4类：结构分析方法、统计方法、基于纹理模型方法和信号处理方法[3]．结构分析方法是基于纹理基元分析纹理特征；统计方法是通过计算像素的局部特征分析各个灰度级的空间分布，常用的统计特性主要有自相关函数、灰度共生矩阵和灰度梯度共生矩阵等[4-5]．基于纹理模型的方法是假设纹理按某种模型分布，如马尔可夫链和马尔可夫随机场模型[6]，通过求解模型参数来提取纹理特征．信号处理方法则是通过对纹理图像进行变换和滤波来提取相关谱特征．

随着小波理论的发展，其在纹理特征提取方面得到了广泛关注[7-8]．近年来，Ojala等提出的局部二进制模式以其计算复杂度小，具有多尺度特性和旋转不变特性，在纹理检索领域得到广泛应用[9-10]．除此之外，由于小波包继承了小波变换所具有的良好时频局部化的优点，能够在全频带对信号进行多层次的频带划分，能够获得更加全面的纹理信息[11-12]．

纹理特征的提取对纹理分类的正确率至关重要．然而，实际获得的纹理图像往往会受到天气、照相设备等因素的影响，这在很大程度上降低了纹理分类的正确率，限制了各种纹理分类方法在实际工程中的应用．渐晕是光照分布不均匀的一种典型表现形式，它指的是相机在远距离成像时，随着视场角的增大，能通过照相物镜成像的斜光束截面面积逐渐减少，从而导致影像中间亮、边缘暗，严重时会在图像的四角产生阴影，影响图像的主观质量[13-14]．渐晕现象会对提取的纹理特征造成很大影响，进而影响纹理图像的分类效果．为解决这一问题，笔者尝试利用渐晕系数，在高频和低频分别对提取的纹理特征进行补偿，以最大限度地减少渐晕现象对纹理特征指数的影响，提高纹理分类的正确率．

1 渐晕模型

渐晕图像可以认为是正常图像本身与渐晕效果相互影响的结果，可以利用一定的方法将二者抽取出来分别进行研究．根据Kang等[14]的渐晕模型，图像中的渐晕效果V(x，y)可以表示为

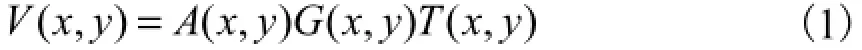
式中：A( x, y)为离轴照明因子，A( x, y)=1[1+(r f )2]2; r为像素点(x，y)距图像中心点的距离；f为照相机的有效焦距长度；G( x, y)代表几何因子，G( x, y)=1-αr，α为几何系数；T( x, y)为倾斜因子，，其中参数χ和τ分别表示平面场景表面绕轴平行于该光学轴的平面的旋转角度，以及这个旋转的平面相对于中心轴的旋转角度．

2 基于小波包分解提取纹理指数

基于小波包分解是目前比较有效的纹理指数提取方法，通过对LL、LH、HL和HH等4个频带图像分别处理，充分利用了纹理图像的细节信息，能够形成有效的特征矢量，获得较高的纹理分类准确率[11-12].函数Wn( x)( n=0,1,2)的小波包函数可表示为

式中：W0(x)是尺度函数；W1(x)是小波函数．

将纹理图像进行L级小波包分解，可以得到4L个大小为MN的子频带图像，可以根据式(3)和式(4)分别计算出各个子频带的均值和方差，即

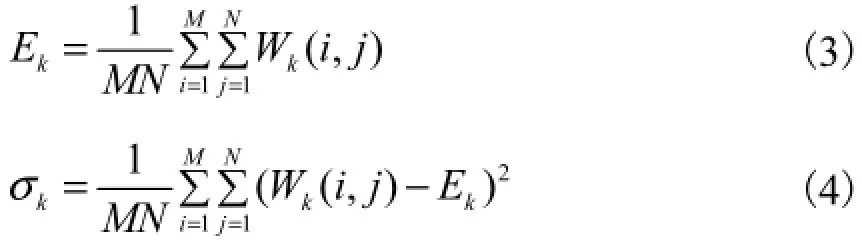
式中Wk( i, j)是小波包分解后第k个子频带的系数，k=1，2，…，4L．将所有子频带的均值和方差构成一个长度为2×4L的一维向量，即T=[E1,…,E4L,σ1,…,σ4L]，将其进行归一化处理后，可以作为描述纹理图像的特征向量．

3 本文方法

基于小波包分解方法提取的纹理特征，能够很好反映标准纹理图像的具体特征．然而，当光照分布不均匀时(如发生渐晕现象)，提取的纹理特征值会产生较大的偏差．笔者拟根据获得的渐晕系数来自动调整相关纹理指数，以解决上述问题．

3.1 纹理特征提取及特征向量的构造

渐晕是一种整体变化的过程，它对图像小波包系数的影响主要体现在低频信息方面，而对高频信息影响较小；因此，与低频信息相比，受渐晕影响较小的高频信息更能准确地反映出图像自身纹理的真实情况．对一幅图像而言，高频信息主要集中在边缘、轮廓和某些纹理的法线上，代表了图像的细节变化，可以认为小波包变换的各高频子带是图像中边缘、轮廓、纹理等细节信息的体现，而且各个子带代表的细节信息的方向是不同的，其中HL代表了水平方向上的边缘、轮廓和纹理，LH表示的是垂直方向的边缘、轮廓和纹理，而对角线方向的边缘等信息则集中体现在HH子带中．根据小波包变换具有的良好的空间方向选择性，以及纹理等细节信息大多集中在高频子带，对不同分辨率下的小波包分解系数分别进行处理，以使得处理后的小波包各子带系数能够尽可能准确地表达图像纹理自身的特征，减少渐晕现象对分类准确率的影响．首先选用高斯型高通滤波器对小波包各子带系数进行调整，以减小特征值对图像低频信息的依赖，获得可靠的高频信息．

渐晕模型能够在很大程度上反映出图像中各点受影响的程度，以及各像素点对纹理系数所做贡献的有效性；除此之外，低频与高频信息与对应图像的各频段信息亦存在一定的相关性．因此，可以根据渐晕的低频及高频信息来调整对应图像区域的相关信息．具体做法是：对渐晕模型与图像同时进行小波包变换，得到二者的各频段信息；然后根据小波包变换后的渐晕效果的低频及高频系数，分别对纹理图像的低频及高频系数进行修正，使之能够更加有效地反映图像的纹理特征，减少渐晕对纹理指数的影响．

将得到的渐晕模型与渐晕纹理图像分割成互不重叠的25张图像，对每张图像进行L级小波包分解，得到4,L个子频带图像，对每个子图像的小波包低频分解系数进行调整，即

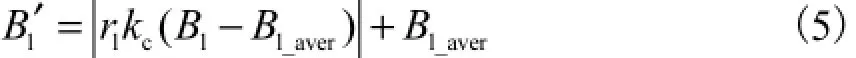
式中rl=1-(VLL_1-VLL_2)VLL_aver，VLL_1、VLL_2和VLL_aver分别代表与图像对应的渐晕模型图像进行小波包分解后，LL3子带系数的最大值、最小值和平均值．从式(5)中可以看出，渐晕越明显，VLL_1和VLL_2相差越大，对低频系数调整的力度也越大；无渐晕发生时，影响因子rl趋近于1，即低频系数基本不变；Bl和Bl'分别代表对图像进行小波包变换后，LL3子带及其调整后的系数，Bl_aver代表LL3子带上小波包系数的平均值，kc是调节因子；对图像其他含有高频信息的子带系数调整方法为

式中：rh=1+(Vother_1-Vother_2)Vother_aver，Vother_1、Vother_2和Vother_aver分别代表与图像对应的渐晕图像进行小波包分解后，含有高频信息的区域系数的最大值、最小值和平均值．Bh和B'h分别代表图像进行小波包变换后含有高频信息的子带系数及其调整后的系数；wh和wl分别代表水平权系数和垂直权系数，只有高频分量时二者分别取值为1和0，既有高频又有低频分量时二者取值均为1．渐晕效果越明显，影响因子rh越大，即对系数调整力度越大；无渐晕效果时，rh趋于1．

经过系数调整后，分别计算出各子图像的均值和方差，构建长度为2×4L的一维向量作为对应纹理图像的特征向量，即T=[E1,…,E4L,σ1,…,σ4L]．

3.2 算法流程

将纹理图像分为训练集和测试集，然后利用式(5)和式(6)分别对渐晕图像的小波包系数进行调整，构建纹理特征指数，利用训练集纹理指数构建SVM的最优分类模型，最后利用SVM实现对不同测试集中纹理图像的自动分类．

算法的具体流程如下：

(1) 提取渐晕纹理图像的渐晕模型[15]．

(2) 将渐晕纹理图像与渐晕模型分别分割成互不重叠、均匀大小的25张图像作为样本，按相同规则随机分为训练样本集和测试样本集．

(3) 利用小波包对纹理图像和渐晕模型的训练样本集的各子图像进行分解，得到相应的小波包系数，分别用式(5)、式(6)对纹理图像的低频子带系数和含有高频信息的子带系数进行调整．

(4) 依据式(3)、式(4)分别计算经过调整的小波包系数的均值和方差，构建纹理图像的特征向量，并对构建的特征向量进行归一化处理．

(5) 将步骤(2)～(4)得到的特征向量作为SVM的输入，寻找最优分类面，建立分类模型，判定该未知样本的类别．

(6) 对分类结果进行统计和分析．

4 实验结果

实验选取国际标准Brodats纹理图像集中的36类纹理图像，另外选取36张实际拍摄的渐晕图像，且渐晕图像的大小与纹理图像大小相同，为640× 640．基于Kang Weiss模型，利用文献[15]方法估计其渐晕模型，估计的渐晕模型参数分别为：χ=0.3，τ=0.6，f=250，α=0.001．由实际渐晕图像得到36种渐晕模型，将其分别添加到36类纹理图像中，形成渐晕纹理图像．

图1(a)表示通常情况下获得的渐晕图像；图1(b)是从实际渐晕图像中提取的渐晕模型；图1(c)是理想情况的均匀纹理图像；图1(d)是在原始理想纹理图像的基础上，依据渐晕模型形成的渐晕纹理图像．

将渐晕模型和对应的渐晕纹理图像分别分割成互不重叠的25张子图像，每张子图像大小为128× 128．采用3级小波包分解，利用36个渐晕模型各子图像的小波包系数，分别对其对应的纹理图像各子图像的小波包变换系数进行调整．在每类渐晕纹理图像的子图像中随机选用10张子图像作为训练样本，余下的15张子图像作为测试对象，即训练样本数为10× 36=360，测试样本数为15× 36=540；基于小波包提取纹理特征向量，将归一化后的特征向量作为SVM的输入，训练和测试SVM，记录分类正确率．

图1 渐晕模型及相关图像Fig.1 Vignetting models and related images

本文选用目前常用的灰度共生矩阵、灰度梯度共生矩阵、统计几何特征、局部二进制模式、小波包分解等纹理特征提取方法与SVM相结合，分别对原始纹理图像和渐晕纹理图像进行特征提取和自动分类，其分类正确率如表1所示．

表1 纹理图像和渐晕纹理图像的分类正确率Tab.1 Classification accuracy of texture images and vignetting images

从表1中可以看出，对于原始纹理图像而言，现在常用的纹理特征提取方法，可以提取较为有效的特征值以达到较高的纹理分类正确率；而对于添加渐晕效果后的纹理图像，由于受到渐晕的影响，利用现有各种纹理特征提取方法，图像分类正确率均比原始纹理图像有明显下降，其中灰度共生矩阵方法下降最少，局部二进制模式方法下降最多，达到了8.15%，整体分类效果均不理想．而利用本文方法对小波包各频段系数进行调整后，对渐晕纹理图像的分类正确率达到了95.19%，明显高于现有方法，取得了比较理想的分类效果．实验中，SVM选用高斯径向基核函数，图2显示了本文方法提取特征向量结合SVM进行分类测试的过程．

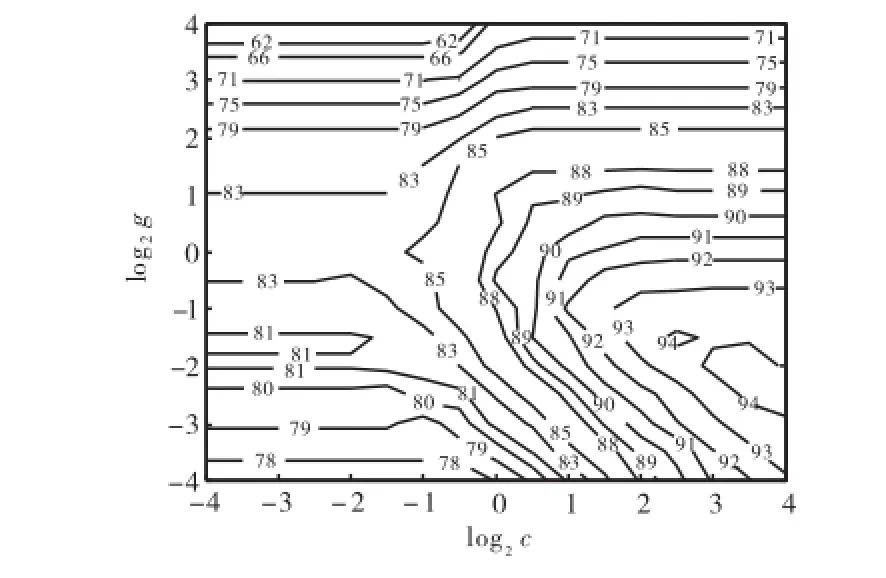
图2 本文方法结合SVM进行纹理自动分类Fig.2 Texture classification by proposed approach combined with SVM

图2 中，纵坐标表示SVM的高斯径向基核函数中参数g的对数值，横坐标表示控制对错分样本惩罚的程度c的对数值．在利用SVM进行分类实验的过程中，上述参数的取值会在很大程度上影响最终的分类正确率；SVM能够自动寻找最优参数，以实现最高的分类正确率．

在自动寻优过程中，2个参数不断变化，对应不同的分类正确率，在图中形成分类正确率的等值曲线，如图中曲线上的数值所示．实验的图像样本经过SVM的参数寻优进行分类，最终可以实现95.19%的分类正确率，此时对应横纵坐标分别为log2c=3.50，log2g=-2.00，即2个参数的取值分别为：c=11.31，g=0.25．

5 结 语

通过对渐晕纹理图像的各频段小波包分解系数进行调整，减小了渐晕现象对纹理特征指数的影响，提高了纹理图像的分类正确率．仿真实验结果表明，与传统纹理特征提取方法相比，本文方法对渐晕纹理图像能够获得更高的分类准确率，取得了比较理想的分类效果．

［1］ Tou J Y，Tay Y H，Lau P Y. A comparative study for texture classification techniques on wood species recognition problem[J]. Natural Computation，2009，l5：8-12.

［2］ Liu Li，Fieguth Paul. Texture classification from random features[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，34(3)：574-586.

［3］ Jing Yitou，Yong Haurtay，Phooi Yee Lau. Recent trends in texture classification：A review[C] // Symposium on Progress in Information and Communication Technology. Kuala Lumpur，Malaysia，2009：63-68.

［4］ 薄 华，马缚龙，焦李成. 图像纹理的灰度共生矩阵计算问题的分析[J]. 电子学报，2006，34(1)：155-158.

Bo Hua，Ma Fulong，Jiao Licheng. Research on computation of GLCM of image texture[J]. Chinese Journal of Electronics，2006，34(1)：155-158(in Chinese).

［5］ Zou Jian，Lin Chuancai. Texture classification by matching co-occurrence matrices on statistical manifolds[C] // 2010 IEEE 10th International Conference on Computer and Information Technology. Bradford，West Yorkshire，UK，2010：1-7.

［6］ Reddy B V R，Mani M R，Subbaiah K V. Texture classification method using wavelet transforms based on gaussian markov random field[J]. International Journal of Signal and Image Processing，2010，1(1)：35-39.

［7］ Wang Z，Yong J. Texture analysis and classification with linear regression model based on wavelet transform[J]. IEEE Transactions on Image Processing，2008，17 (8)：1421-1430.

［8］ Huang Y，Wang L，Li C. Texture analysis of ultrasonic liver image based on wavelet transform and probabilistic neural network[C] // International Conference on Biomedical Engineering and Informatics. Sanya，China，2008：248-252.

［9］ Shang Y，Hou W，Wu R，et al. Anti-noise rotation invariant texture classification based on LBP features of dominant curvelet sub-bands[C] // Intelligent Information Technology Application. Shanghai，China，2008：365-369.

［10］ Liao S，Law M W K，Chung A C S. Dominant local binary patterns for texture classification[J]. IEEE Transactions on Image Processing，2009，18(5)：1107-1118.

［11］ Murat Karabatak M，Cevdet Ince，Abdulkadir Sengur. Wavelet domain association rules for efficient texture classification[J]. Applied Soft Computing，2011，11 (1)：32-38.

［12］ 孙洁娣，靳世久. 基于小波包能量及高阶谱的特征提取方法[J]. 天津大学学报，2010，43(6)：562-566.

Sun Jiedi，Jin Shijiu. Feature extraction method based on wavelet packet energy and high-order spectrum[J]. Journal of Tianjin University，2010，43(6)：562-566 (in Chinese).

［13］ Zheng Yuanjie，Kambhamettu Chandra，Lin Stephen. Single-image optical center estimation from vignetting and tangential gradient symmetry[C] // IEEE Conference on Computer Vision and Pattern Recognition. Florida，USA，2009：2058-2065.

［14］ Kang Singbing，Weiss Richard. Can we calibrate a camera using an image of a flat textureless lambertian surface? [C] // European Conference on Computer Vision. London，UK，2000：640-653.

［15］ Zheng Yuanjie，Lin Stephen，Kang Sing Bing. Singleimage vignetting correction[C] // IEEE Computer Society Conference Computer Vision and Pattern Recognition. New York，USA，2006：461-468.

An Automatic Classification Approach to Vignetting Texture Images

He Kai，Zhang Weiwei，Kong Xiangwen
(School of Electronic Information Engineering，Tianjin University，Tianjin 300072，China)

Since traditional texture classification methods are usually sensitive to lighting condition, non-uniform light distribution, such as vignetting, will greatly reduce the classification accuracy of texture images. To solve this problem, this paper presented a new approach to automatic classification of vignetting texture images. By extracting texture features with the wavelet packet decomposition algorithm, vignetting coefficients were utilized to adjust the wavelet packet coefficients obtained, thus eliminating the effect of vignetting on texture features, and consequently improving texture classification accuracy. Experimental results show that the approach proposed in this paper can significantly improve classification accuracy and achieve ideal texture classification effect.

texture classification；feature index extraction；vignetting model；wavelet packet transform；support vector machine

TP391

A

0493-2137(2013)06-0526-05

DOI 10.11784/tdxb20130610

2011-10-27；

2012-02-02.

国家自然科学基金资助项目(61271326，61002030).

何 凯（1972— ），男，副教授．

何 凯，hekai626@163.com.