R统计软件在统计教学中的应用*

杨宜平，赵培信

（1.重庆工商大学数学与统计学院，重庆400067;2.河池学院数学系，广西宜州 546300）

随着计算机的普及以及统计软件的发展，在经济、生物、工业等诸多领域正在采用统计软件分析数据，因而单纯的讲授统计理论的教学方式已不能适应当今社会发展的需求，将统计软件的实际应用与理论教学相结合的教学是现代统计教学的必然趋势。在进行统计分析时，常用的统计软件有R、SAS、SPSS、S-Plus等。在Tiobe公布的2011年11月编程语言排行榜上，R语言位列第27位，市场占有率是0.5%，为统计软件之首。由于R统计软件具有其他统计软件所不具备的优点［1-4］，加之R软件完全免费，因此，受到广大统计研究人员和统计工作者的青睐。在此以回归模型为例介绍R统计软件在统计教学中的应用。

1 回归分析

在进行统计分析时，回归分析运用十分广泛，它是建立两种或者两种以上变量间相互依赖的定量关系的一种统计分析方法。现主要介绍线性回归模型和分位数回归模型。

1.1 线性回归模型

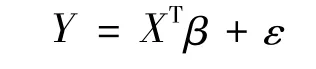
其中Y为n×1的向量，X为p×n的矩阵，ε是n×1随机误差向量，其均值为0且Cov（ε）=σ2I，则回归系数β的最小二乘估计为

在R统计软件中，拟合线性回归模型的函数为lm（），例如建立Y与X1和X2的回归模型，

如果想了解更多关于函数lm（）的用法，可输入:

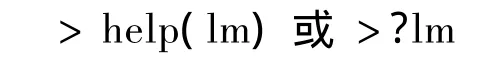
可以查到该函数的用法。

1.2 分位数回归模型

Koenker和Bassett［5］在1978年提出了分位数回归，其思想是建立因变量Y对自变量X的条件分位数回归模型。X对Y的线性分位数回归模型

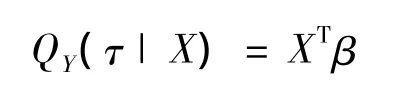
其中τ是因变量Y在X条件下的分位数。XTβ是拟合Y的第τ分位数。特别地，如果τ=0.5就是中位数回归。为了获得回归系数的估计，需最优化问题:

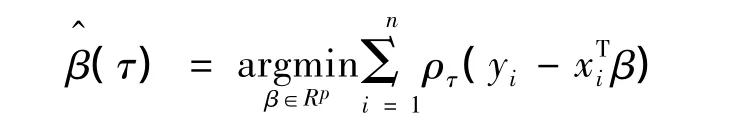
其中 ρτ（u）=τuI［0，∞）（u）－（1 －τ）uI（－∞，0）（u）。目前对该最优化问题有3 种算法:单纯形算法、内点算法和平滑算法。在文献［6］中，对这3种算法进行了详细的论述。

Roger Koenker编写了分位数回归的程序包“quantreg”。先到R主页上把包下载下来，然后安装该程序包。如何安装R包，文献［1，2］中有详细介绍。安装该程序包后，拟合分位数回归的函数为rq（），其调用格式为

当tau值缺省时为0.5，表示中位数回归。输入help（rq）可以进一步了解该函数的功能以及调用格式。

1.3 线性回归与分位数回归比较

王星［2］将传统的线性回归模型与分位数回归模型进行了比较。传统的线性回归模型具有以下缺陷:传统线性回归模型建立的是均值回归模型，只反映均值变化;模型误差需满足Gauss-Markov假设条件，假设条件太强。在许多实际问题研究中不满足该假设条件，如等方差假定就很难满足。

分位数回归克服了线性回归模型的一些缺陷，与线性回归相比，分位数回归具有以下优点:分位数回归是拟合不同分位数水平下的估计值，反映更多信息;不需要对随机误差做具体的假定;对异常值不敏感，拟合结果比较稳定。

2 教学案例

为测量某种材料的保温性能，把用其覆盖的容器从室内移到温度为X的室外，3 h后记录其内部温度Y。经过11次试验，记录数据见表1。

表1 某种材料室外与内部温度记录数据 ℉

分别采用线性回归和中位数回归分析该数据集。对该数据集进行分析时，参考R语言程序如下:

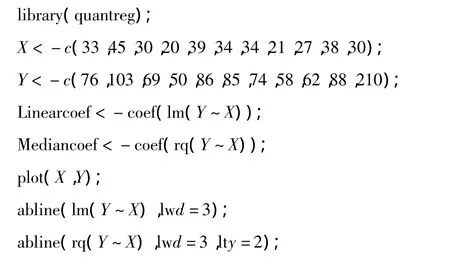
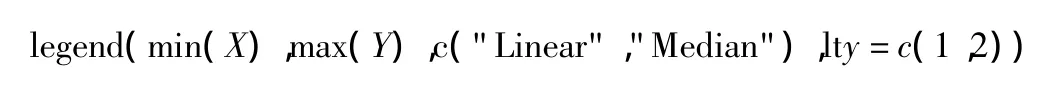
从图1可以看出线性回归和中位数回归的差异。线性回归受到异常点影响较大，中位数回归对异常点不敏感，拟合结果较稳定。

3 结束语

数据分析已成为很多科研人员以及行业机构关注的热点之一，而基于统计方法分析数据是其中关键技术之一，专业统计软件的出现为人们分析数据提供了有力支撑。统计学是一门应用性很强的学科，在教学过程中，在为学生讲授专业理论知识时，应结合实际统计案例，并采用统计软件进行相关数据分析，以加深学生对于统计思想的理解。以线性回归模型和分位数回归模型为例介绍了R统计软件在统计教学中的应用，通过案例来阐述R统计软件对这两种回归模型的具体操作。案例和统计软件辅助教学的方式，不仅加深了学生对统计思想和方法的理解，而且激发了学生的学习兴趣，进一步提高了学生解决实际问题的能力。

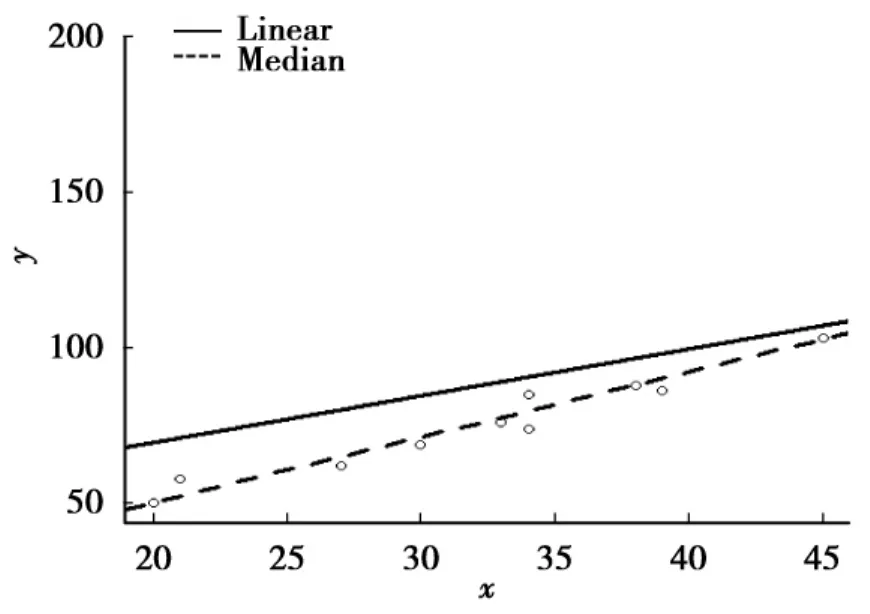
图1 某种材料保温性能的中位数回归（虚线）和线性回归（实线）

［1］薛毅，陈立萍.统计建模与R软件［M］.北京:清华大学出版社，2006

［2］王星.非参数统计［M］.北京:清华大学出版社，2010

［3］王斌会.多元统计分析及R语言建模［M］.广州:暨南大学出版社，2010

［4］汤银才.R语言与统计分析［M］.北京:高等教育出版社，2005

［5］KOENKER R，BASSETT G W.Regression quantiles［J］.Econometrica，1978，46（1）:33-50

［6］陈建宝，丁军军.分位数回归技术综述［J］.统计与信息论坛，2008，23（3）:89-96