基于自适应猴群算法的传感器优化布置方法研究
伊廷华,张旭东,李宏男
传感器的合理选择与优化布置是建立结构健康监测系统首先应解决的关键科学问题。从理论上讲,在结构上安置的传感器越多,所获取的结构振动信息也就越详细;然而由于经济因素和现场条件等多方面的原因,在结构的所有自由度上布置传感器是不可能的,也是不现实的;且过多的传感器也会引入许多冗余数据,对结构响应信息的高速存储与有效分析带来困难。一种好的传感器布设方案应满足[1-2]:在含噪声的环境中,能够利用尽可能少的传感器获取全面而精确的结构响应信息;测得的结构响应信息应能够与数值分析的结果相对应;对感兴趣的振动响应数据进行重点采集;监测结果具有良好的可视性和鲁棒性;监测系统的设备投入、数据传输、结果处理的费用达到最少。
国外对传感器优化布置的研究起步较早,Kammer[3]早在1991年就对大型空间结构传感器的优化布置问题提出了著名的有效独立法;模型缩减法也是一种常用的传感器布置方法,主要通过删除对模态响应作用不大的自由度,将剩余的自由度作为传感器的布设位置[4];Heo等[5]将测点获得结构运动能最大作为传感器的优化目标,提出了基于运动能量法的布设方法。在国内,宗周红等[6]对以模态置信度矩阵和以Fisher信息阵标准为理论基础的传感器优化布点算法进行了详细地分析研究;伊廷华等[7]提出了基于简化模型的传感器优化布置的算法,解决了由于空间耦合振动,难以准确选取弱轴模态振型的难题。传统的传感器布置方法基本上是通过某种迭代的方式对初始的候选传感器布置位置进行消去或者增加,尽管这类方法非常有效,但其得到的结果却是次优的,即通过此类方法得到的传感器布置位置无法保证真实的与实测的信息之间的误差最小。众所周知,传感器优化布置是一种组合优化问题,即整数规划的问题,由于组合优化问题十分复杂,它的求解仍是许多学者研究的方向。近几年,一些随机智能优化算法,如模拟退火、遗传算法、蚁群算法、粒子群算法等相继出现,因其能够较好地解决组合优化问题中约束条件的限制且不易陷入局部最优等特点而在传感器优化布置领域取得了较快地发展。刘明辉[8]从免疫系统原理出发,结合遗传算法提出了一种基于二次选择的免疫遗传算法,比较了几种抗体浓度构造方式在免疫遗传算法中的作用,并将该算法应用于桁架结构的优化中,收到较好的效果;伊廷华等[9]对比研究了简易遗传算法和广义遗传算法的特点,并对广州新电视塔的传感器布置进行了研究,给出了不同的优化布设方案;谢建红等[10]采用遗传神经网络算法对压电智能结构进行了传感器优化布置,对具体的实现过程及其可行性进行了分析,结果表明了其是可行的;Menon等[11]采用模拟退火算法研究了振动控制中传感器的优化布置以用于模型相关分析,取得了较为理想的结果;Rao等[12]对粒子群算法进行了改进,使其适用于传感器优化布置问题,并将其应用到大型空间结构的传感器优化布置,优化效果令人满意。
任何一种智能算法在提出时都有其特定的适用范围,将其引入到传感器优化布置中应在满足解决此类问题限定条件的基础上加以改进以提高其计算效率。本文基于一种新型智能算法:猴群算法(Monkey Algorithm,MA)[13],提出了一种用于传感器优化布置的自适应猴群算法(Adaptive Monkey Algorithm,AMA),赋予了猴子在爬过程和望过程中的自适应能力,来增强算法的局部搜索能力;并引入两种全新的跳方式,来增强算法的全局搜索能力;文末通过一个工程算例验证了该方法的可行性和有效性。
1 基于自适应猴群算法的传感器优化布置方法
MA是通过模拟猴子爬山过程中爬、望和跳过程而提出的一种全新的智能算法。该算法假定有M只猴子爬山,每只猴子从自己所处的位置出发,以一定的步长aa往山上爬(假定目标函数为求最大值,求最小值时可加上负号),当爬到自己所处领域最高处时,以视距ba向周围进行瞭望,如果在周围能找到比自身位置更高的山峰则翻到此山峰;当爬和望过程进行到一定次数后,每只猴子以所有猴子的重心进行跳过程,跳到新的位置后继续进行爬过程。
爬过程和望过程是MA中逐步改善优化问题中目标函数值的过程,贯穿于整个算法的搜索过程之中,其效率的高低直接影响到算法的有效性。原MA中爬过程和望过程是分开进行的,当猴子爬到一定的高度之后,才进行望过程,然后再继续进行爬过程,这种寻优过程十分机械,搜索效率不高;此外,原MA的跳过程只是简单的以重心为支点跳,这种方式能够达到新区域的概率有限,极有可能错过全局最优解的位置。基于此考虑,且受生物自适应能力的启发,本文对原猴群算法进行了改进,让爬过程和望过程同步进行,使猴子能够根据周围环境的变化自动选择爬和望过程,即在局部搜索过程中根据爬过程和望过程的好坏,自适应地选择其中一种方式进行搜索;并提出了两种新的跳方式,以多种跳方式共同产生最优解,大幅提高了算法的搜索性能。
1.1 编码方式及初始化
传感器优化布置问题是一类特殊的背包问题,原MA只能求解连续变量的优化问题,对于求解传感器优化布置这种0-1规划问题,由于伪梯度不能给出下降的搜索方向,从而会导致爬过程失效,使得算法无法进行。本文提出一种双重编码的方法在AMA中进行解的表达,即利用有序对(x,c)表示猴子个体来对应传感器布置问题的可行解(其中,x为AMA中的位置向量;c为二进制向量,表示传感器的布置位置),较好地解决了这一问题。相应的编码过程及算法初始化方式如下:
步骤1:建立欲布置传感器结构的有限元模型,通过模态分析得到所有候选测点的振型矩阵,将各阶振型含有的节点位置作为优化布置的候选资源。假设传感器的所有候选布设位置为f,则对各个候选位置进行编号,对应到1~f的整数。
步骤2:以猴群中的第i只猴子为例,其相应的解可表示为 xci=(xi,ci)={(xi,1,ci,1),(xi,2,ci,2),…,(xi,f,ci,f)},f为设计变量的个数(即全部自由度的数目),各分量对应相应候选资源的编号,位置向量xi的各个分量为从区间[down,up]之间随机产生的整数,本文取down=-5,up=5;ci为xi中的各元素通过下式转换而得到的二进制编码向量:

采用(1)式时,需要首先设定一个判断阈值ε;若sig(xi,j)≤ε,则该分量 ci,j取 0(即表示在该编号即 j的位置处不布置传感器);若sig(xi,j)>ε则该分量的取1(即代表在该位置上即j位置上布置传感器)。这里j∈{1,2,…,f},本文取 ε =0.5,通过计算可以发现,当 xi的各分量在[-5,5]之间取值时,0.006 7≤sig(xi)≤0.993 3,且变化均匀,因此本文这种取值方法是合理的。
步骤3:通过步骤1和步骤2随机产生M只猴子的位置(M即为猴群的规模)。假设欲布置传感器数目为n,对于初始化产生的解,相应ci中传感器位置的数量可能会出现不等于n的情况,即出现违法编码的情况,则此时应重新初始化,即返回步骤2。
每只猴子的解即对应一个候选的优化布置方案。以第i只猴子为例,其目标函数记为f(xi,ci),本文提出的AMA在迭代过程以位置向量xi进行迭代,通过sig函数将其转换为二进制向量ci,再根据ci中所确定的传感器布设位置计算目标函数值,根据其值的好坏进行相应地迭代搜索。
1.2 自适应爬过程和望过程
爬过程和望过程是MA中主要的局部搜索步骤,其搜索效率的高低对算法的性能具有重要的影响。通过对原MA分析可以发现,猴子必须经过大量的爬过程,当达到所要满足的高度以后才进行望过程的操作,这种迭代过程十分机械。这种迭代方式会造成两种情景:第一,在爬山的过程中,猴子周围随时会出现比自己目前正在爬的山峰更高的山峰,而原MA设计的思想是“全然不顾身边的风景”,猴子必须到达正在爬的山的山顶以后才进行望的过程,可以说是一种“盲目”的爬。实际上,猴子在遇到更高的山峰时完全可以通过望过程直接跳过去,这样不仅可以节约时间,还可以遍历搜索所在区域的山峰;第二,猴子可能通过很少次数的爬过程就已经到达所在区域的山峰了,但由于迭代过程还没有结束,猴子不得不在山顶上来回的爬动,等达到预先设定的迭代终止条件后,才能看看周围的“风景”(即是否周围有更高的山峰),这使得算法的效率非常低。基于此考虑,且受自然界生物自适应特性的启发,本文提出的AMA的思想是让猴子在爬的过程中不断的瞭望,若望到比自身更好的位置,则直接跳过去,然后在新的山上继续进行爬过程和望过程。具体实施方法如下:
(1)爬过程
以第 i只猴子的当前位置 xi=(xi,1,xi,2,…,xi,f)为例,本文设计的爬过程迭代步骤如下:
步骤1:随机从区间[-aa,aa]中产生整数 Δxij,组成向量 Δxi=(Δxi1,Δxi2,….,Δxif)T,这里 j∈{1,2,…,f},aa称为爬步长。
步骤2:由xi+Δxi和 xi-Δxi得到猴子两个新的位置向量xnew1和xnew2,分别计算此时两个新位置的目标函数;若猴子两个新的位置中任何一个位置比之前的位置好,则猴子的位置向量即变为此,若两个新位置都比之前的位置好,则选择两者中最好的位置作为猴子新的位置向量,否则猴子的位置保持不变。
(2)望过程
以第 i只猴子的当前的位置 xi=(xi,1,xi,2,…,xi,f)为例,定义猴子的视距为ba,本文设计的望过程步骤为:
步骤1:在区间[xij-ba,xij+ba]内随机产生整数xwij,j∈ {1,2,…,f},得到此猴子新的位置 xwi=(xwi,1,xwi,2,….,xwi,f)T。
步骤2:计算猴子新位置的目标函数值,若变好,即望到的新山峰更高,则以xwi作为望过程得到新位置,否则返回步骤1。
基于以上爬过程和望过程,本文设计的自适应爬过程和望过程的步骤如下:
步骤1:以xi为初始位置,进行爬过程,达到预定的爬过程次数Nc1,由此得到新的位置为xc。
步骤2:以xi为初始位置,进行望过程,若望到比自身好的位置xw则停止。
步骤3:步骤1和步骤2这两个过程同步进行,猴子根据xc和xw位置的好坏,选择其中的一个过程的结果作为新的位置,然后再进行下一步操作。
步骤4:重复步骤1至步骤3,直至达到自适应爬过程和望过程的次数Ncw。
注1:在上述步骤中,计算 xi+Δxi或 xi- Δxi,得到新的猴子位置向量中的分量有时会出现“溢出”的情况,即会跌出位置向量的取值范围[down,up]的情况。因此,这里规定:新的分量如超过上限up,则取值up;若小于down,则取为down。本文其他的迭代步骤遇到类似情况做相同的处理。
注2:本文假设布置传感器的数目为n,若在迭代过程中出现c向量各分量的全部之和不等于n(即出现违法编码的情况),则此时迭代过程停止,回到起点重新进行开始,直到满足条件为止。本文后面的跳过程遇到类似情况也同样处理。
1.3 跳过程
跳过程主要是为了让猴子从当前的搜索区域转移到新的搜索区域,然后在新的区域内重新进行迭代搜索,以避免算法陷入局部最优,这是保证算法能得到全局最优解的关键步骤。原MA设计的跳过程思想只是简单的以猴群的重心为支点,让猴子沿着当前的位置指向支点的方向,跳到各自相对应的新的搜索区域内,这种方式不能以较大概率保证猴群遍历全部搜索区域,特别是对于解决传感器优化布置这种具有复杂的多维解空间的问题,易遗漏掉全局最优解的位置。基于此考虑,本文在原MA跳过程的基础上,提出了两种全新的跳过程(反射跳和变异跳),以期通过多种跳的方式来增大猴子所能达到的搜索区域,使得算法能够以更高的概率找到全局最优解。
(1)原始跳过程(s1)
定义跳区间为[ca,da],它决定了猴子跳过程中所能到达的最大范围,对于第i只猴子,设此时位置向量xi=(xi,1,xi,2,…,xi,f),设计相应的 s1 步骤如下:
步骤1:在跳区间[ca,da]内随机产生实数θ。
步骤2:计算该猴群位置向量各分量的重心,取paj这里 j∈{1,2,…,f},可得到猴子跳的支点 pa=(pa1,pa2,…,paf)T。
步骤 3:计算 xs1i,j=xi,j+round(θ|paj- xi,j|),其中j∈{1,2,…,f},得到新的猴子位置 xs1i=(xsi,1,xsi,2,…xsi,f),round 为取整函数。
步骤4:计算新位置的目标函数值,若更好,则跳向该位置,取猴子的新位置为xs1i;否则返回步骤1。
(2)反射跳过程(s2)
本文提出的反射跳的思想源于单纯形算法中的反射算子[14]。原反射算子的产生过程,首先从种群中选出一定数量的个体,然后去掉最差适应度的个体,此最差个体记为xw;并计算剩余个体的重心位置向量,记为xp,最后通过公式(2)计算得到xw相对于xp的反射点,以改变xw的位置进入其他区域,以此达到以更大的概率找到全局的最优解。

从公式(2)可以看到,这种反射点的产生只是改变最差解的位置,本文考虑传感器优化布置的特点(即每个传感器布设的位置重要性等同),对其过程进行适当的改进,提出了一种将每只猴子的位置都进行反射的反射跳过程,具体如下:
步骤1:以第i只猴子为例,设此时猴子的位置向量为 xi=(xi,1,xi,2,…,xi,f);并计算全部猴子的重心位置向量,记为 pa=(pa1,pa2,…,paf)T。
步骤2:对该猴子按公式(3)进行反射跳过程的计算:
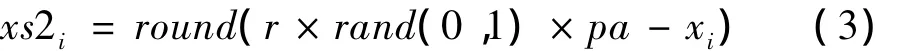
式中:rand(0,1)是随机产生(0,1)之间的随机数;round为取整。
通过计算可以发现,当r取4时,式(3)可适合双重编码方式进行迭代搜索的过程。
步骤3:由步骤1步骤2即可得到该猴子通过反射跳跳到的新位置xs2i。
(3)变异跳过程(s3)
本文提出的变异跳的思想源于遗传算法中的变异操作[15],其方式是通过对选择的个体以一定的概率随机改变串结构数据中某个串的值。变异操作为新个体的产生提供了机会,增加了种群的多样性,有利于防止种群出现“早熟”现象,即陷入局部搜索过程,本文将其思想引入跳过程中。设第i只猴子的位置为xi=(xi,1,xi,2,…,xi,f),引入变异概率 sar,以该猴子第 j个变量xi,j为例,设计变异跳步骤如下:
步骤1:随机产生 r1=rand(0,1),即产生(0,1)之间的随机数。
步骤 2:如果 r1 < sar,则 xs3i,j= - xi,j,否则 xs3i,j=xi,j,j∈{1,2,…,f}。
步骤3:对该猴子的位置循环每个变量,则可得到该猴子进行变异跳过程跳到的新位置xs3i。
以第i只猴子为例,综上三种跳的方式,本文设计AMA中的跳过程如下:
步骤1:分别由s1、s2、s3跳过程使该猴子进入到三个不同区域新位置 xs1i、xs2i、xs3i。
步骤2:该猴子以此三个位置分别进行自适应爬、望过程进行重新搜索。
步骤3:对于所有猴子都进行步骤1和步骤2过程。
算法经过自适应爬过程、望过程以及跳过程一次循环,则算法搜索过程终止,将最优解作为最后的传感器布置位置。
2 优化目标函数的选择
目标函数是对所优化问题目标的数学描述,本文提出的基于AMA的传感器优化布置在迭代过程中直接以目标函数的值来评价新解的优劣。由结构动力学的原理可知,结构各阶模态向量在节点上值形成了一组正交向量。当量测自由度远小于结构模型的自由度且由于受到测试精度和测量噪声的影响,使得测得的模态向量很难保证其正交性,在极端的情况下甚至会出现由于向量间的空间交角过小而丢失重要模态的情况。因此,在选择测点时有必要使量测的各模态向量保持较大的空间交角,Carne等[16]认为模态置信度矩阵(Modal Assurance Criterion,MAC)是评价模态向量空间交角的有效工具,其表达式为:
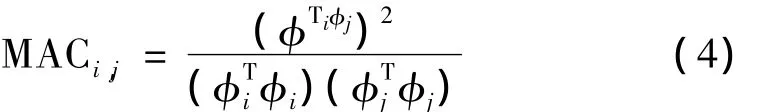
式中:φi和φj分别为振型向量矩阵中的第i阶和第j阶模态向量。
由式(4)可以发现,MAC矩阵中非对角元MACi,j(i≠j)能够反映两模态向量之间的交角,其值越小,各阶测试自由度振型的独立性越好,传感器布置效果也就越好;反之,各阶测试自由度振型相关性越大,传感器布置效果越差。因此,测点的布置可采用MAC矩阵的非对角元最小化为目标函数。其表达式为:

3 工程算例
3.1 工程简介及计算模型
为了检验本文提出方法的有效性,这里以在建的大连国际贸易大厦(图1(a))为例,对其进行传感器优化布置研究。大连国贸大厦位于大连市中心商业区的友好广场附近,地下建筑5层,地上建筑79层,建筑主体高度达到330.25 m,建成后将成为我国东北地区最高的建筑物。大厦的塔楼采用外钢管混凝土框架-内混凝土核心筒的结构形式,采用三维高层建筑结构专业软件ETABS对大厦进行建模(图1(b)),并进行模态分析[17]。考虑结构两个主轴方向刚度差别非常大,这里选取弱轴方向为传感器的布设方向,其简化模型如图1(c)所示,选取结构的前8阶振型进行计算分析。

图1 大连国际贸易大厦Fig.1 Dalian international trade mansion
3.2 基于AMA的传感器优化布置研究
利用本文提出的AMA算法对大连国贸大厦布置25个传感器时的位置进行优化研究,即n=25。考虑模型有79个候选测点位置,因此f=79,各个测点用1~79相应的整数编号表示,在计算过程中采用本文给出的双重编码方式进行解的表达和迭代搜索。
为了验证本文提出的AMA的有效性,同时采用以下两种工况进行对比分析:
工况1:采用原MA进行传感器优化布置研究(即采用简单的爬、望、跳过程进行传感器优化布置)。
工况2:采用本文提出的AMA进行传感器优化布置研究。
(1)参数敏感性分析
在进行传感器优化布置之前,首先应考虑控制参数AMA算法的影响,即分析控制参数的敏感性,以便为下一步选取的合适的参数的做参考。选取影响AMA性能的3个重要参数进行分析:爬过程循环次数Nc1;自适应爬、望过程循环次数Ncw;由于无法通过参数分析来验证s1和s2两种跳过程对算法的影响,这里选择变异跳s3过程中的重要参数变异概率sar来进行参数分析。将参数 Nc1,Ncw,sar分别设置为 10、20、40;50、100、200;0.1、0.4、0.7 三个水平,通过正交试验设计构成正交试验表,如表1所示。表1中括号内为设置水平数,在进行计算时其他参数(取爬步长为aa=1,望过程ba=2,设计其原始跳跳区间为[-3,3])不变,共构成9组工况进行,参数分析结果如表1所示。
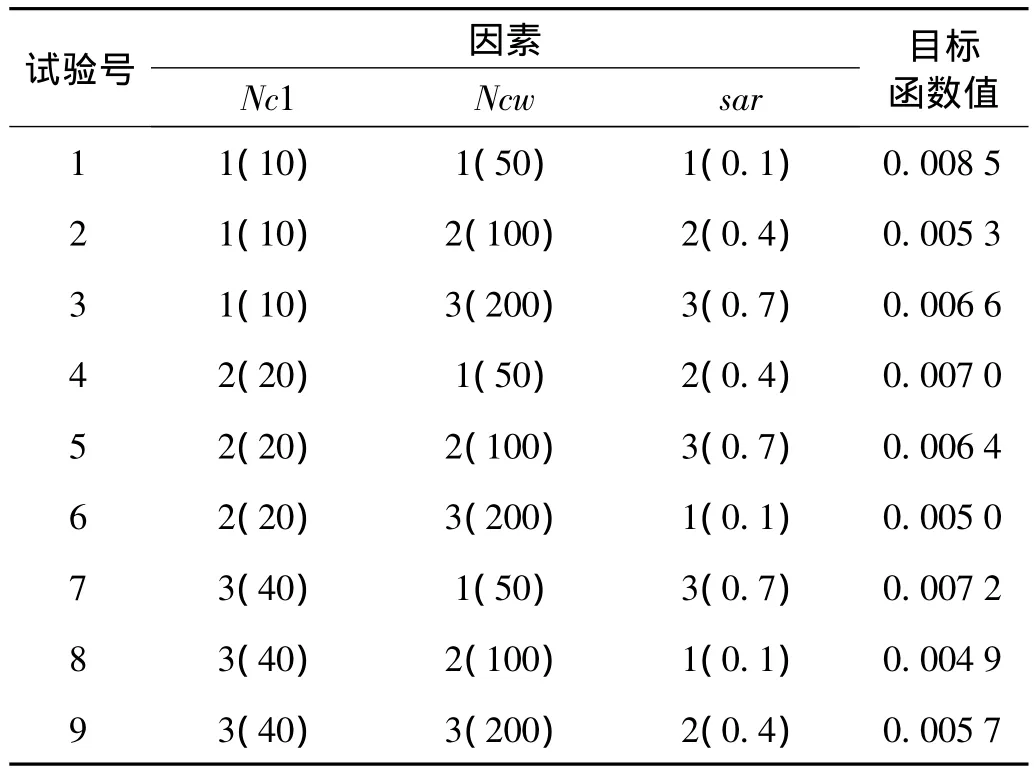
表1 正交试验表及试验结果Tab.1 Orthogonal table and test results
从参数分析表1中可以看出:①AMA算法的搜索结果很好。随着Nc1的变化,即简单的爬过程次数的变动,计算结果有一定的波动性,并不是随着Nc1增大结果变的越好,这说明本文对原MA机械的爬过程效率较低的推断是正确的,可以看到Nc1取值在20左右比较合适。②随着Ncw的增加,计算结果改善较为明显,验证了本文提出的自适应爬过程和望过程的有效性;但过大的Ncw对计算结果提升并不是很明显,其值选为100左右较为合适。③变异概率sar对算法的计算结果影响较大,随着变异概率的变化,计算的结果有一定的波动,但从整体上来看,变异概率0.4到0.7之间取值比较合适。基于以上参数分析,本文对大连国贸大厦进行基于AMA的传感器优化布置时的参数设置如下:取猴群中猴子的数量为M=5;考虑本文采用的双重编码迭代的特点,取爬步长为aa=1,望过程ba=2,设计其跳区间为[-3,3];取爬过程循环次数为Nc1=100,自适应爬、望过程循环次数为Ncw=20;通过取不同的值进行了一定数量的计算,确定本文变异概率取sar=0.5。工况1中爬过程循环次数取为2 000。
(2)优化布置结果分析
表2给出了各种传感器布置方法的目标函数值。图2(a)给出了工况1即采用原MA算法布置25个传感器时的MAC矩阵柱状图,此时非对角元最大值最为最大值为0.004 8,而此时全部自由度的MAC非对角元为0.023 9,这说明对于结构所有的自由度都布置传感器并不一定能得到最优布置效果;工况2较工况1计算结果提高了66.7%,效果很明显,说明本文提出的基于AMA的算法十分有效。由于图2中MAC非对角元的柱状图的非对角元都非常小,为了更加清晰地体现本文提出算法的有效性,这里给出了每阶模态列向量非对角元最大值的比较,如图3所示。从图3中可以清晰的看出,本文提出的AMA算法的在列向量MAC非对角元最大值绝大多数都比MA算法得到的结果小,这较好地验证了本文提出算法的有效性。大连国贸大厦采用AMA布置25个传感器得到的布置方案如表3所示。

表2 不同传感器布置方案的目标函数值Tab.2 Objective function value of each kind of sensor placement

图2 由工况1和工况2得到的MAC值Fig.2 MACvalues obtained by case 1 and case 2
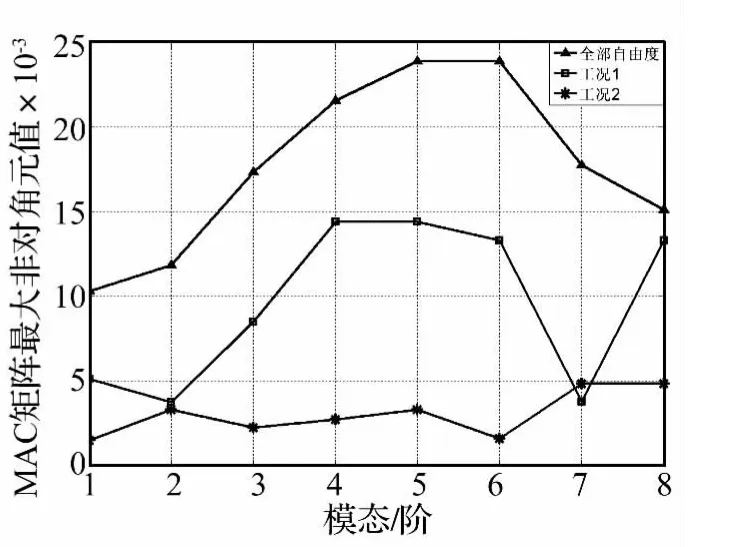
图3 每个模态列向量MAC非对角元最大值Fig.3 Maximum MAC off-diagonal value in each of the modes

表3 大连国贸大厦传感器优化布置方案Tab.3 Sensor placements of the Dalian international trade mansion
4 结论
本文针对原MA中的爬过程和望过程较为机械的问题,提出了一种基于AMA的传感器优化布置方法,并以一超高层建筑为例,得到了以下结论:
(1)本文采用双重编码方式有效地克服了原MA只能解决连续变量优化的问题,计算分析结果表明,该方法能将传感器优化布置问题与猴群算法很好地衔接起来。
(2)原MA中爬过程和望过程非常机械,搜索效率较低,易错失局部最优解的位置,针对此问题并受自然界中生物的自适应能力的启发,本文提出了自适应爬、望搜索的思想,即通过不断地同步进行爬、望过程来增加算法局部搜索能力。考虑原MA跳过程的单一性,有可能错失全局搜索的位置,本文提出了两种全新的跳过程,即反射跳和变异跳过程,增强了算法的全局搜索能力。
(3)控制参数分析表明,不同的参数取值对AMA的搜索性能有一定的影响,增加自适应爬和望过程的次数,搜索性能会随之有所提高;增加爬过程循环次数,算法的计算效果变化较小,说明原MA中简单的进行爬过程之后再进行望过程的效率较低,这体现了本文提出的自适应爬、望过程的有效性;变异跳过程中的变异因子对计算结果有一定波动的影响,说明加入变异跳过程的有效性。
(4)以大连国贸大厦为例,采用MAC矩阵非对角元最大值作为目标函数对其传感器优化布置进行了对比研究,结果表明:本文提出的AMA的搜索性能较原MA有了大幅提高,适于解决此类问题。
[1]伊廷华,李宏男,顾 明.基于模型缩聚的广州新电视塔传感器优化布置研究[J].工程力学,2012,29(3):55-61.YI Ting-hua,LI Hong-nan,GU Ming.Research on optimal sensor placement of Guangzhou new TV tower based on model reduction[J].Engineering Mechanics,2012,29(3):55 -61.
[2]伊廷华,李宏男,顾 明,等.基于MATLAB平台的传感器优化布置工具箱的开发及应用[J].土木工程学报,2010,43(12):87-93.YI Ting-hua,LI Hong-nan,GU Ming,et al.Development of MATLAB based optimal sensor placementtoolbox and its application[J].China Civil Engineering Journal,2010,43(12):87-93.
[3]Kammer D C. Sensor placement for on-orbit modal identification and correlation of large space structures[J].Journal of Guidance,Control Dynamics,1991,14(2):251-259.
[4] Penny J E T,Friswell M I,Garvey SD.Automatic choice of measurement locations for dynamic testing[J].AIAA Journal,1994,32(2):407 -414.
[5]Heo G, Wang M L, Satpathi D. Optimal transducer placement for health monitoring of long span bridge[J].Soil Dynamics and Earthquake Engineering,1997,16(7 -8):495-502.
[6]宗周红,孙建林,徐立群,等.大跨连续刚构桥健康监测加速度传感器优化布置研究[J].地震工程与工程振动,2009,29(2):150 -158.ZONG Zhou-hong,SUN Jian-lin,XU Li-qun,et al.Study on optimal placement of acceleration sensors for health monitoring of a long-span continus rigid-frame bridge[J].Journal of Earthquake Engineering and Engineering Vibration,2009,29(2):150 -158.
[7]伊廷华,李宏男,王国新.基于简化模型的超高层结构传感器优化布置[J].计算力学学报,2008,25(4):417 -423.YI Tin-hua,LI Hong-nan,WANG Guo-xin.Optimal sensor placement for super high-rise building based on simplified finite elemet modal[J].Chinese Journal of Computational Mechanics,2008,25(4):417 -423.
[8]刘明辉.免疫算法原理应用研究及机翼结构布局优化[D].西安:西北工业大学,2006.
[9]伊廷华,李宏男,顾 明.结构健康监测中基于多重优化策略的传感器布置方法[J].建筑结构学报,2011,32(12):217-223.YI Ting-hua,LI Hong-nan,Gu Ming.Multiple optimization strategies based sensor placement method for structural health monitoring[J].Journal of Building Structures,2011,32(12):217-223.
[10]谢建宏,张为公.压电智能结构损伤检测传感器优化配置的遗传神经网络方法[J].传感技术学报,2007,20(2):413-418.XIE Jian-hua,ZHANG Wei-gong.GANN method applied to optimize sensor placement based on damage detection for piezoelectric smart structures[J].Chinese Journal of Sensor and Actuators,2007,20(2):413 -418.
[11] Menon R G,Browder A M,Kurdila A J,et al.Concurrent optimaization of piezoelectric actuator locations for disturbance attenuation[C].Proceedings of SDM Conference,AIAA - 93-1689-cp,1993:3269-3278.
[12] Rao A R M,Anandakumar G.Optimal placement of sensors for structural system identification and health monitoring using a hybrid swarm intelligence technique[J].Smart Materials and Structures,2007,16(6):2658 -2672.
[13] Zhao R Q,Tang W S.Monkey algorithm for global numerical optimization[J].Journal of Uncertain Systems,2008,2(3):165-176.
[14] Nelder J, Mead R. A simplex method for function minimization[J].Computer Journal,1965,7:308 -313.
[15]Yi T H,Li H N,Gu M.Optimal sensor placement for structural health monitoring based on multiple optimization strategies[J].The Structural Design of Tall and Special Buildings,2011,20(7):881 -900.
[16] Carne T G,Dohmann C R.A modal test design strategy for modal correlation[C].Procedings of the 13th International Modal Analysis Conference,Schenectady,New York,USA,February,1995.
[17] Li H N,Yi T H,Jing Q Y,et al.Wind-induced vibration control of Dalian international trade mansion by tuned liquid dampers[J].Mathematical Problems in Engineering,2012,Article ID 848031:1-20.

