抽样调查偶然断尾资料的样本选择模型分析*

胡乃宝 徐天和 王 玖

受限反应变量

抽样调查的目的是用样本信息推断总体特征，样本要具有代表性，即是随机样本。但在实践中，常常有部分观测单位因为多种原因出现空缺，即无应答(nonresponse)，这时抽样调查得到的就是失随机性样本。抽样调查失随机性可以分为个体无应答和项目无应答，后者是指被调查者虽然接受了调查，但是仅仅回答了问卷的一部分，不能得到某些项目的信息。项目无应答表现在数据层面就是变量缺失〔1〕。如果回归分析中的反应变量部分缺失，即反应变量的取值范围受到限制，称为“受限反应变量”(limited dependent variable)。受限反应变量主要包括断尾数据(truncated data)、删失数据(censored data)以及偶然断尾数据(Incidental truncation data)等几种情况。如果数据只有在某个区间才能被观察到，称为断尾数据。例如反应变量为某市所有医院的年效益，而统计部门只收集一定规模以上的医院的数据，这样年效益低于标准的医院的数据就不能被观测到，此时反应变量存在“左端断尾”(left truncation)，同样存在“右端断尾”(right truncation)、“区间断尾”(interval truncation)。对于删失数据而言，虽然收集到全部数据，但某些观察值却被压缩到一个点上。例如，流行病学随访研究中，在规定的观察期内，某些观察对象由于某种原因未能观察到终点事件发生，得不到确切的生存时间，即生存时间的删失数据;删失包括“右删失”(right censoring)、“左删失”(left censoring)和“区间删失”(interval censoring)。偶然断尾又称为样本选择，假设反应变量的断尾受其他变量的影响，如在糖尿病生存质量的研究中，全部患病人群中会有一定比例的病人由于种种原因(如疾病严重程度)不会进入研究范围。

此类基于反应变量缺失获得的样本就用到了受限反应变量模型(limited dependent variable model)。三种受限反应变量对应着三种模型:断尾回归模型(truncated regression model)、删失回归模型(censored regression model)和样本选择模型(sample selection model)〔2〕。本文只介绍样本选择模型在偶然断尾数据中的应用。

样本选择模型原理及参数估计的stata实现

样本选择模型〔3〕的结构是:

其中，反应变量Yi是否能被观察到取决与指示变量Di，di为与指示变量相关联的潜变量，yi是与反应变量 Yi相联系的潜变量。假设 εi～N(0，σ2)，μi～N(0，1)，其相关系数为corr(εi，μi)。由于μi～N(0，1)，所以Di服从 Probit模型，即P(Di=1|Z)=Φ(γZi)。这样可以写出观测样本的条件期望:

其中，λ(－γZi')为“逆米尔斯比率”，λ(－γZi')=通过上述推导可以看出，如果用最小二乘法进行参数估计将会遗漏非线性项 ρσελ(－γZi')，除非误差项相关系数为0，否则将会导致有偏估计。Heckman和 Gronau〔4〕率先给出了样本选择模型的似然参数估计，该方法对误差项分布做出假设:εi和vi服从正态分布，且(εi，vi)相互独立，然后通过构造对数似然函数来估计参数。Lee Lung Fei〔5〕于1982年提出了仅要求εi和vi的边缘分布已知，利用逆标准正态分布函数将ε和v的边缘分布转换为标准正态分布，然后用似然估计的参数方法。A.R Gallant和D.W Nychka〔6〕于1987年提出了不需要误差项分布信息的半参数似然估计。似然估计参数法要求误差项服从双变量正态分布或者需要误差项的边缘分布信息，而半参数方法需要较为高深的数学理论且计算较为复杂，所以推广较为困难，在实际应用中不常见。最为常见的方法是Heckman提出的两步估计:第一步:用Probit估计方程P(Di=1|Z)=Φ(γZi)，得到估计值^γ，并计算^λ(－^γZi');第二步:做yi对Xi和^λ的普通最小二乘估计，得到^β、^ρ和^σ的估计值。

stata 9.0以上版本有专用模块来实现样本选择模型的两步估计和似然估计〔7〕。程序格式:

程序1:

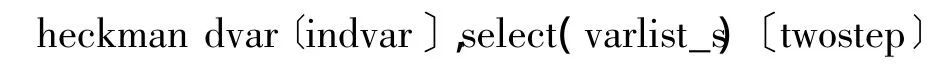
程序解释:其中，dvar代表反应变量的名称，indvar代表自变量的名称。选项select()为必选项，它用来确定选择方程的反应变量及自变量。varlist_s的变量用于决定原方程的反应变量dvar是否被观测到。选择方程的varlist_s至少应包含一个与前面方程不同的自变量。

或者，程序2:

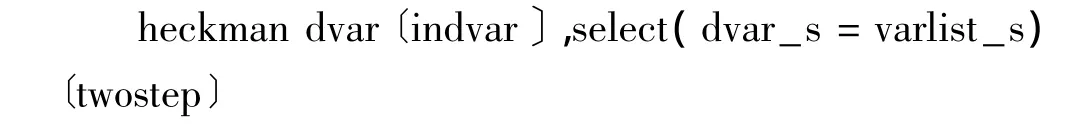
程序解释:设定方程的反应变量dvar_s，要求dvar_s的值必须为0或者1。0表示原方程的反应变量没有被选择，1表示被选择。如果采取程序1，不设定选择方程的自变量，则系统默认原方程的反应变量dvar非缺失值时即表示被选择，缺失值时没有被选择。

如果设定twostep选项，系统使用两步法进行回归参数的估计，缺失默认使用最大似然估计。

实例分析

女性工资水平的影响因素可能与文化程度、年龄等因素有关，但是只有她们选择工作时才能观察到其工资水平。她们是否工作并不是随机的，受其保留工资以及工资数量影响，保留工资受婚姻状况和孩子数量的影响，工资数量受教育程度和年龄的影响。很显然我们只能收集到参加工作的女性的工资水平，无法收集到没有选择工作的女性的工资水平，这样就发生了样本选择偏倚，应该应用样本选择模型分析数据。选取1975年美国女性劳动供给数据〔6〕中的1800条记录进行实例分析，资料包括一般人口学资料和工资水平。变量赋值为:Y=工资收入(单位:千美元/年)、edu=文化程度(上学年数，单位·年)、age=年龄(岁)、married=婚姻状况(0=未婚，1=已婚)、children=孩子数量。资料中工资缺失952例，偶然断尾率为52.89%。应用样本选择模型的极大似然进行参数估计，结果等式ε的标准误为5.93，选择性效应为3.97;对模型假设检验 wald χ2=471.21，P ＜ 0.01，模型中的系数是联合显著的;残差项相关系数 ρ为0.67，差异具有统计学意义(对ρ的似然比检验，χ2=48.01，P=0.00)，资料的样本选择模型似然估计是合适的。具体似然估计结果等式和选择等式的回归系数以及其假设检验结果见表1。

样本选择模型两步估计结果为:ε=5.89，λ=3.84，ρ=0.65，模型检验 wald χ2=516.89，P ＜ 0.01。两步估计的结果等式和选择等式的回归系数以及假设检验结果见表2。

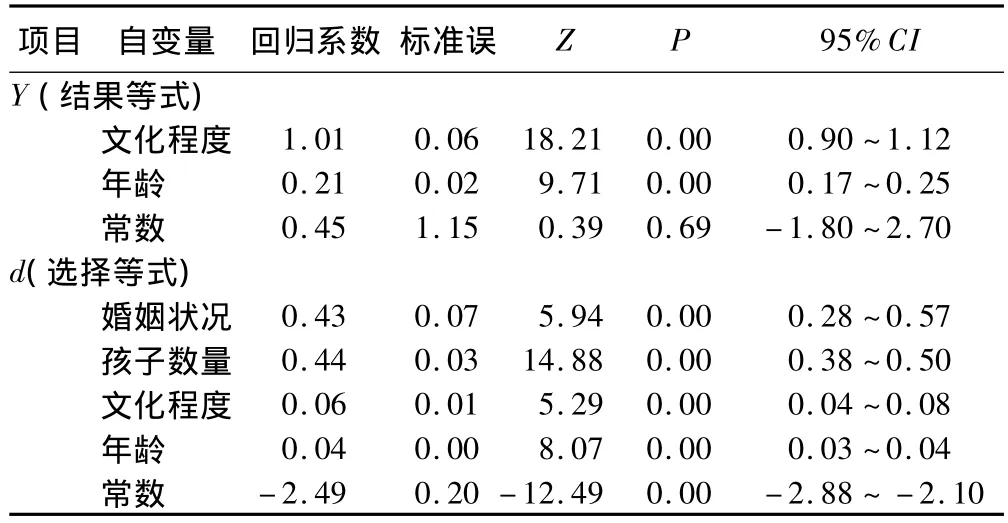
表1 女性工资水平影响因素的样本选择模型极大似然估计结果

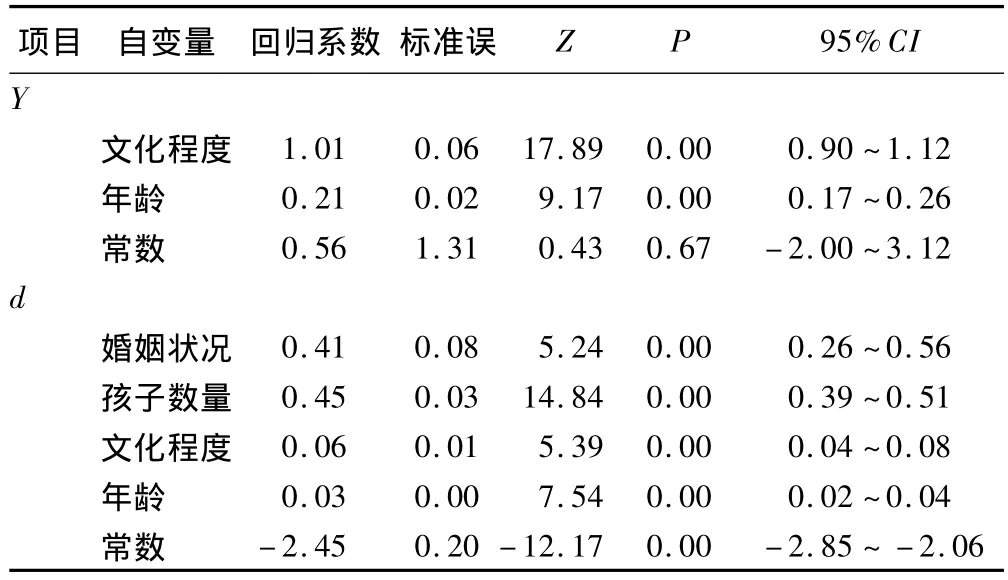
表2 女性工资水平影响因素的样本选择模型两步估计结果

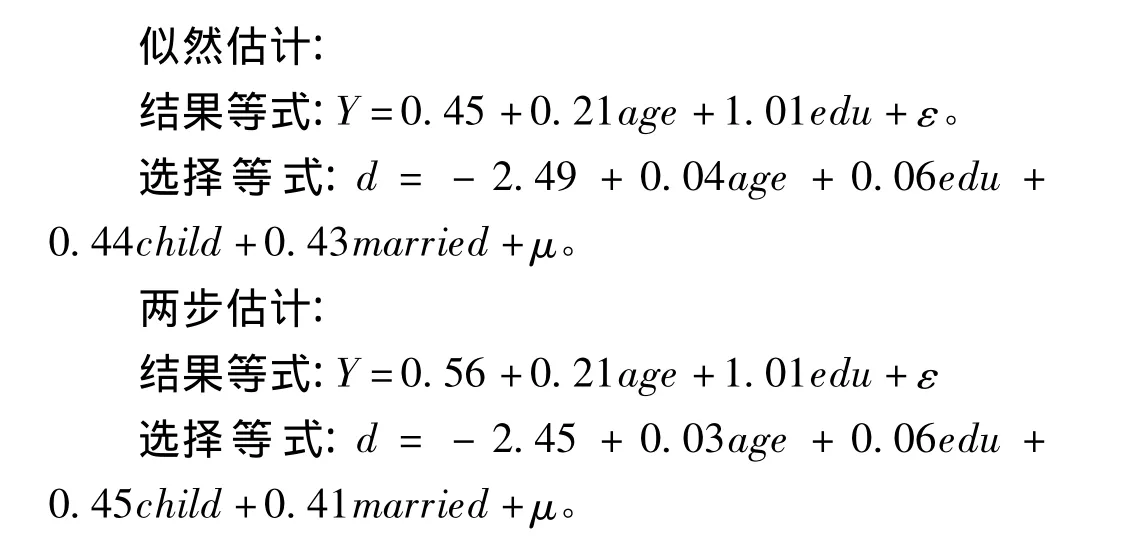
小 结

如果抽样调查的数据缺失不是随机的，而且误差项又是相关的，那么最小二乘法所获得回归系数β是有偏差的〔8〕。本实例中误差项的相关系数 ρ=0.67(χ2=48.01，P=0.01)，工资水平的偶然断尾率为52.89%，最小二乘法不是有效方法。样本选择模型分析结果，女性是否参加工作受婚姻状况、孩子数量、文化程度等因素的影响，且只有潜变量的线性组合值大于0时工资水平才能被观测到，否则为断尾。通过结果等式可见，女性工资水平受文化程度和年龄的影响，在同龄人中上学年限每增加1年，工资水平平均要增加1.01千美元;在文化程度相同的人群中，年龄大者容易得到较高的工资水平。

模拟实验证实断尾程度的大小影响参数估计方法的选择，在轻度断尾的情况下由于样本信息量的损失并不严重，最小二乘法仍然可以得到较为理想的估计量，此时就没有必要应用样本选择模型。由于资料限制，本研究没有对重度和轻度断尾数据进行实例分析。

当数据量比较大时，极大似然估计非常耗时〔7〕。本例对比两步估计结果与似然估计结果，无论是残差相关系数，还是残差的标准误，或者模型假设检验的P值均非常接近，可见两步法对参数估计的确提供了一种很好的替代。而且两步估计还有似然估计不具备的优势:首先，当反应变量存在测量误差时，似然函数的最大似然估计量不一致，而两步估计由于测量误差会被引入结果等式的残差中，所以不会对估计结果产生太大影响〔9〕;其次，似然估计的对数似然函数通常不是全局凹的，无法保证解的唯一;最后，似然函数估计对于参数估计初始值的选择比较敏感。基于此，两步估计已成为样本选择模型参数估计的“最受欢迎程序”。但是有部分学者对两步估计中存在的共线性问题心存疑虑，提出了几种方法:一是岭回归，大量的蒙特卡罗模拟实验证明岭回归能在两步估计第二步时获得较为稳健的估计量;二是适当增加样本含量以增加选择等式中自变量的变异，尽可能的获得非线性校正项来避免共线性问题〔10〕。

本文涉及到的反应变量只是二分类的，对于多分类的样本选择模型可构建多分类probit模型，但是如何反映选择等式与结果等式的联系是很困难的，需要把样本选择模型与离散选择模型结合来进行分析。软件实现方面，SPSS没有专用模块实现样本选择模型的参数估计，而且stata 10.0并没有涉及两步的半参数估计。这些都是以后研究的方向。

1.刘世炜，王春平，杨功焕.调查研究中项目无应答误差的识别与处理.中国卫生统计，2008，25(2):183-186.

2.薛小平，史东平，王彤.受限因变量模型及其半参数估计.中国卫生统计，2007，24(2):211-213.

3.James JH.Shadow prices，market wages，and labor supply.Econometrica，1974，42(4):679-694.

4.Gronau，Ruben.Wage comparisons-A selectivity bias.The Journal of Political Economy，1974，82(6):1119-1144.

5.Lee LF.Generalized econometric models with selectivity.Econometrica，1983，51(2):507-12.

6.Gallant AR，Douglas WN.Semi-Nonparametric maximum likelihood estimation.Econometrica，1987，55(2):363-390.

7.周广肃，梁荣，田金秀，等.Stata统计分析与应用.北京:机械工业出版社，2011:222-230.

8.张磊，王彤.样本选择模型及其估计方法.中国卫生统计，2010，27(6):662-665.

9.David CS，Douglas JY.Censored normal regression with measurement error on the dependent variable.Econometrica，1984，52:737-760.

10.Davidson R，James GM.Estimation and inference in econometrics.Oxford University Press，1993.