环锥型通心浮子流量计研究

许现本 董 群 焦岢迪 鲁 微 肖 辉

(东北石油大学，大庆 163318)

0 引言

浮子流量计结构简单、压力损失小、工作特性稳定、反应灵敏、价格便宜、广泛应用于中小管径、雷诺系数较低的中小流量测量[1]。然而，随着工业界对流量计的准确度等级和测量范围的要求越来越高，浮子流量计的流程局限性逐渐显现并制约着它的应用[2]。因此如何在不增加能耗的基础上，对传统流量计进行改进，增加浮子流量计的量程，降低生产成本，成为浮子流量计研究的热点。

目前，增大浮子流量计量程的方法包括：增加转子质量、采用高密度材料作为转子、加大流通截面等方法[1-3]。这些方法虽然扩大了量程，却也增加了生产成本。研究在原有浮子流量计的基础上，将实心转子进行开孔，设计出一种新型结构的环锥形浮子流量计。目前，国内未见相关报道。

1 工作原理及流量计算公式

环锥形玻璃管浮子流量计的流量检测元件结构示意图如图1所示。流体自左而右流入锥管，被浮子截流，此时作用在浮子上的力有4个：压差力、浮力、重力及黏性应力(黏性流体对浮子壁面产生黏性摩擦力) ，4力平衡时，浮子将平稳地浮在锥管内的某一位置，即对应某一确定流量[4-6]。

通过伯努利方程进行能量衡算，并在计算中忽略流动的能量损失，以流量系数a对其进行校正，新型浮子流量计的流量方程为[7]:

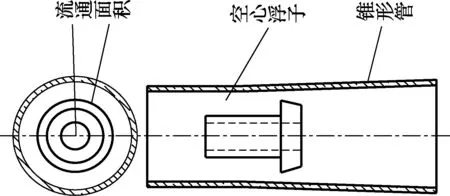
图1 环锥形浮子流量计结构示意图

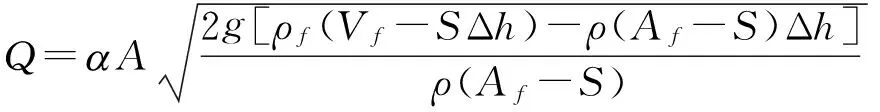
式中：a为仪表的流量系数，通过实验所得；S为开孔面积；m2;A为流通环形面积与开孔面积之和，m2；g为当地重力加速度，m/s2；Vf为浮子体积，如有延伸体亦应包括，m3；ρf为浮子材料密度，kg/m3；ρ为被测流体密度，如为气体是在浮子上游横截面上的密度，kg/m3；Af为浮子工作直径(最大直径)处的横截面积，m2，Δh为浮子的高度，m。流通环形面积与开孔面积之和A的计算公式为：

A=p (dhtanθ+h2tan2θ)+S

式中：d为浮子最大直径(即工作直径)，m；h为浮子从锥管内径等于浮子最大直径处上升高度，m；θ为锥管的圆锥角。

2 通心浮子流量计设计

为研究不同开孔径与流量关系，设计了不同的开孔半径，如图2所示。

图2 不同开孔径的通心浮子

3 CFD仿真计算

3.1 网格划分

采用ansys workbench进行CFD仿真计算，应用solidworks建立环锥型玻璃管通心浮子流量计流体域模型,浮子形状设计如图2所示。利用workbench中mesh模块进行网格划分，采用四面体网格，使用inflation功能对边界层进行网格划分，为了控制网格精度，控制网格质量Skewness最大要小于0.9。

3.2 计算条件

采用湍流模型进行计算，简单又具有较高的精度，采用标准的k-ε模型，壁面采用标准壁面函数，根据有限体积法对方程进行差分离散。流体介质为10℃的水，密度为999.7kg/m3，黏度为1.307×10-3Pa·s。inlet边界条件为velocity；outlet边界条件为pressure。壁面的边界条件为默认值。求解控制参数中，离散格式选择基于压力-速度耦合SIMPLE算法，压力方程使用一阶标准格式，其他方程使用二阶迎风格式，松弛因子为默认0.25[8]。

3.3 仿真数据

通心浮子流量计中通心浮子受到的升力FS等于重力时，inlet的流量为浮子在该刻度的流量。Fluent开始计算后监视残差和升力系数Cl。当残差收敛到10-4且Cl在迭代中平稳不变化，可判断计算结束。使用“浮子受力平衡误度差分析法”逐步调整流量，控制精度。将误差控制为|Ef|≤10%,得到仿真流量Q(如图3所示)。

4 实验验证

为了验证通心浮子流量计能增大流量和数值模拟的计算结果，本研究选取了规格为40L/h的浮子流量计(浮子为铝材质)并制作了紫铜浮子和采用以下的实验流程设计，如图4所示。对通心浮子流量计进行流量测量。分别对图2中不同的开孔半径浮子取位置为65mm处进行测量，每次重复测量3次取平均值[6]。

图3 仿真流量图

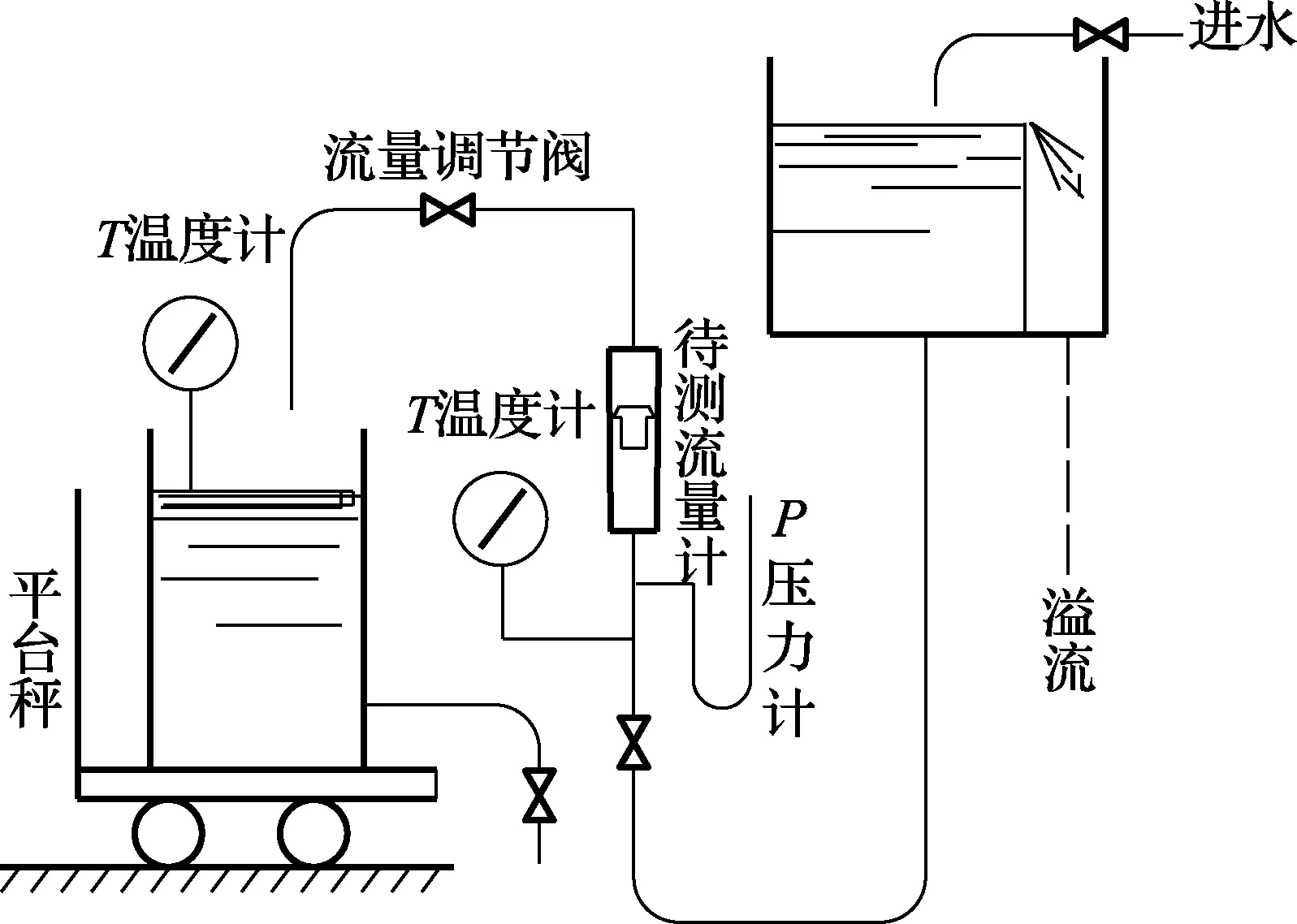
图4 实验装置流程图

5 实验结果与仿真对比分析

5.1 实验结果

实验结果如图5所示。

图5 实验结果流量图

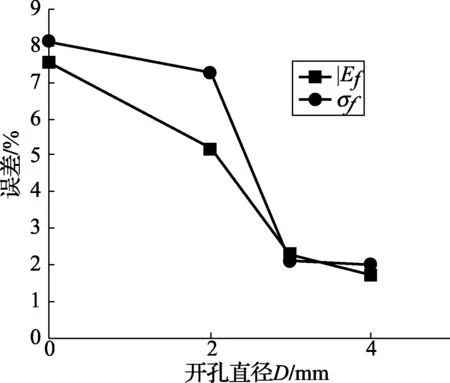
图6 仿真误差分析与结果对比分析

5.2 仿真结果分析

通过仿真可以看出通心浮子流量计能增大流量，由于网格划分的质量，湍流模型的计算精度都有一定的误差，仿真计算流量与实验流量误差σf=(Q实验-Q仿真)/Q实验×100%和升力与重力误差|Ef|，如图6所示。

5.3 速度场分布图分析

图7所示流场图为迭代收敛后的局部速度分布图，视图为三维模型创建x=0的 Iso-surface图，单位为m/s。途中彩色柱体表示速度由上往下递减，每个颜色各自对应Iso-surface图中的速度矢量。

由图可知：速度分布为轴对称分布，从实心到开孔孔径不断增大，流体速度由环隙流通面积最小处最大过渡到孔中流速最大，符合圆管中流体速度从壁面向中心递增理论分析。

图7 流体域模型和浮子流场图

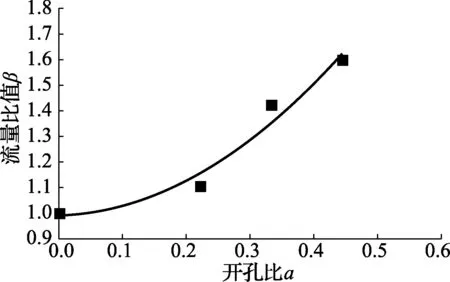
图8 实验结果分析

5.4 实验结果分析

实验的结果表明通心浮子流量计能增大流量并证实了仿真数据的精度。由于实验采用的流场为真实流场，流量测量具有更高的精度，所以采用实验数据研究开孔比a(开孔面积/最大截面积)与开孔后流量与未开孔流量比值θ的关系。图8为比值β与开孔比a的关系。拟合方程为β=3.04178a2+0.06974a+0.99124，残差平方和为0.00844，相关性为0.88992。

6 结论

1)通过计算机仿真和流量实验，可以得到环锥形通心浮子流量计能增大流量计量程；

2)确定开孔比与开孔后流量和未开孔流量比值成β=3.04178a2+0.06974a+0.99124关系；

3)通过分析通心浮子流量计流场图发现开孔直径越大开孔通道的流量越大，当流量过大时影响浮子的稳定性和精度；

4)环锥形通心浮子流量计改进方法简单易行，经济便宜并能达到增大量程的目的，可为一种理想的改进方法。

[1] 朴立华,张涛,马艳芳,王军朋.基于CFD的锥管浮子流量计结构优化[J].传感器与微系统,2011,3(30):90-97

[2] 朴立华,张涛,毕丽红.基于CFD的大口径锥管浮子流量计结构设计[J].天津大学学报,2010,9(43):804-809

[3] 张建智.水平浮子流量计的设计与优化[D].湖南：中南大学,2004

[4] 李良贸,张以民.常用测量仪表实用指南[M].中国计量出版社,1998

[5] 温强.基于霍尔效应的智能金属管浮子流量计的研究[D].天津：天津大学,2002

[6] 徐英，刘正先，张涛.浮子流量计三维湍流流场的数值研究.天津大学学报[J].天津大学学报，2004，37(1)：74-79

[7] 苏峰,张涛,刘欣.浮子流量计方程式的原理分析与修正[J].化工自动化及仪表,2005,32(5):64-67

[8] 朴立华，张涛，马艳芳，王军朋.基于CFD的锥形管浮子流量计结构优化[J].传感器与微系统，2011(3):9-43