非线性时钟温度漂移的二阶修正算法

张 军

(天津市计量监督检测科学研究院，天津 300192)

0 引言

时间同步是网络测控的基本问题[1-2]，受到广泛关注和研究[3-7]。由于各节点时钟的漂移，测控系统必须周期性对钟。而在对钟间期，系统通常运行时间漂移修正算法，以尽可能修正时钟漂移，延长对钟间隔，从而减小节点开销。尤其对于资源受限节点(如传感器网络节点)，高效的时钟漂移修正算法有助于延长节点寿命。

线性时钟漂移修正实现简单，因而被广泛使用。但该算法用于修正非线性时钟漂移效果并不理想。本文首先通过实验数据说明了典型时钟芯片的时间漂移具有非线性特性，之后提出一种二阶时钟漂移修正算法。实验表明该算法能够有效修正非线性时钟漂移。

1 问题导出

时钟通常由晶体振荡器及外围电路构成。限于成本，电子产品的时钟通常由时钟芯片实现。对ADE7569芯片内部时钟进行连续约19天测试，按照温度和施加电压的不同分为4个测试阶段，测试结果见表1。

表1ADE7569内部时钟的漂移

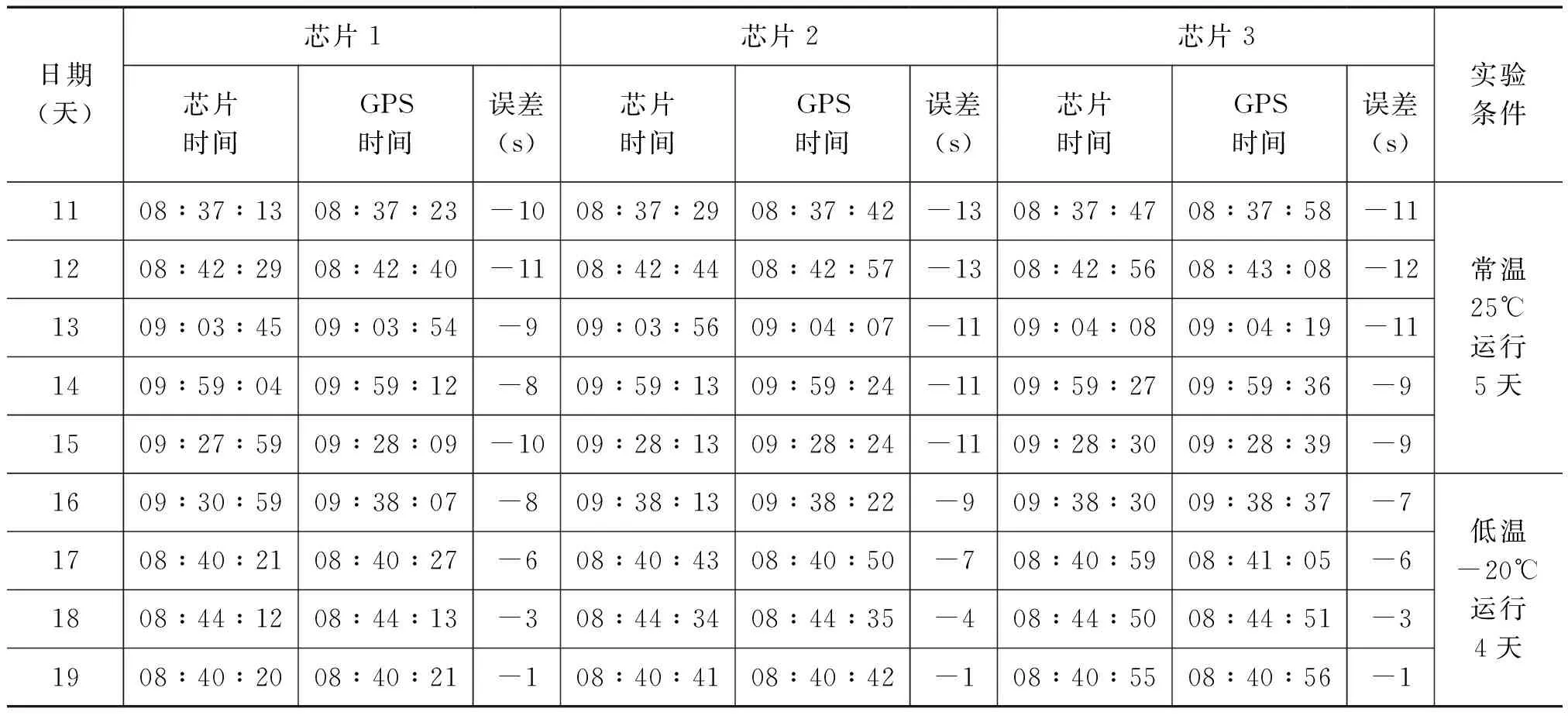
续表

在表1中，将GPS时间视为标准时间，据此计算芯片时间的误差。图1为芯片1、2、3的平均累计漂移曲线。

由图1和表1表明，ADE7569芯片在55℃下具有非线性累计漂移，漂移率为负；25℃下具有非线性漂移，漂移率随时间增加；-20℃下具有线性累计漂移率，漂移率近似为正常数。

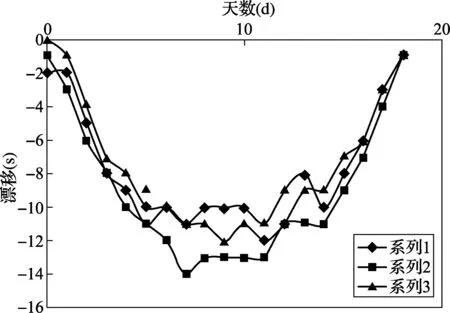
图1 ADE7569内部时钟的累计漂移

由于时钟漂移导致计时误差的积累，因此，为维持时钟误差处于可接受范围，必须周期性对钟。提供参考时间的时钟为主时钟，需要对钟的时钟为从时钟。所谓对钟即从时钟通过一定方式获取主时钟时间，并据此调整自身时间的过程。为了延长从时钟对钟间隔，从时钟在对钟间期通常运行时间误差修正算法，以减缓计时误差的积累速度。而常规的线性误差修正算法在处理非线性时钟漂移时效果不甚理想。

2 二阶修正算法

第i个同步周期[tS,i,tS,i+1)内，从时钟(本地时钟)在tS,i时接收主时钟(源时钟)tM,i。假定tS,i与tM,i之间存在如下非线性关系：

(1)

式中，δ为偏移项；ρ为漂移率，(1+ρ)构成线性项系数；l为平方项系数；r(tS)为随机项。根据拉格朗日二阶插值公式[8]得到各项的估计方法如式(2)、式(3)和式(4)所示。计算过程中存储器必须保存最近的r+2k个时间对[tM,i,tS,i]。本文取r=64，k=8。

(2)

(3)

(4)

误差修正的步骤如下：

1)第i个时间同步周期开始，从时钟获取当前的[tM,i,tS,i]，并保存最近的r+2k个时间对。

2)根据式(3)和式(4)获取式(1)中相应项系数的估计值。

3)利用第2)步结果，根据式(5)计算当前从时钟时间。

(5)

(6)

(7)

对钟结束。第i+1个周期开时跳转0。

经过上述步骤得到的本地时间仅在对钟阶段保持较高准确度，随时间推移，误差呈增加趋势。为在整个周期内都能获得高度准确的时间，还需执行式(8)修正算法。在同步周期[tS,i,tS,i+1)内，[tS,i,tS,i+T)为对钟阶段，采取线性修正算法，须使修正后的时间数值单调增长，T是对钟所需的计算时间；[tS,i+T,tS,i+1)为修正阶段，采取二阶修正算法。在修正阶段，二阶算法较线性修正具有较小误差(图2中粗实线表示修正后的本地时间)。

(8)

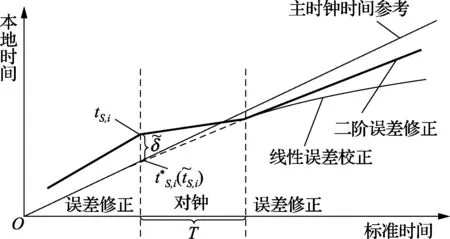
图2 对钟与时间误差修正

3 实验

3.1 实验装置

在图3所示测试系统中，控制板CB1作为主时钟，CB2、CB3、CB4作为从时钟，都配置有以太网接口，四者通过交换机经由以太网相连。CB1安装有GPS模块，可以获取GPS时间。CB1～CB4通过测试连接与时间频率计相连。但由于时间频率计同时只能比较两个输入信号的时间间隔，所以，在时间频率计与CB1～CB4之间插入多路选择器。该设备在监控主机控制线实现对任意一对测试连接线路的选取。监控主机通过仿真连接控制CB1～CB4，实现对时间同步参数的设定以及数据的读取。监控主机通过GPIB总线与时间频率计相连，读取两条测试连接线输入的脉冲信号时间差。CBn工作于50MHz，从而硬件计时器拥有80ns的分辨率。时间按频率计HP53132A拥有150ps的分辨率。

图3 测试系统组成

3.2 实验结果

实验在25℃下进行，分别采用本文提出的二阶修正算法和常规线性修正算法，得到两组实验结果。从表2及图4可知，应用二阶修正算法后时钟在8天内的漂移小于1s，而在使用线性修正算法的情况下(表3、图5)，8天内的漂移大于2s。

表2二阶修正时间采样(25℃)

续表

图4 二阶修正时间采样(25℃)

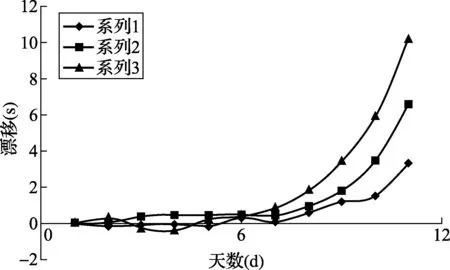
图5 线性修正采样(25℃)

表3线性修正时间采样(25℃)

从上述图表中可以看出，长期内二阶修正算法较线性修正算法具有更好的修正效果。

4 结论

时间同步问题是分布式测控系统的基本问题，也是网络化数据采集和应用分析的基础问题。本文通过实验数据说明了时钟漂移的基本变化规律：环境温度对漂移性质有着显著的影响，且漂移率一般为非线性。针对非线性时间漂移，提出了对钟间期的二阶修正算法。该算法利用二阶差分估计修正公式的平方项。试验表明二阶误差修正算法在修正时钟非线性漂移时较线性误差修正算法有明显的优势。

[1] B.Simons，J.L.Welch，and N.Lynch，An Overview of Clock Synchronization.1988

[2] B.Patt-Shamir，and S.Rajsbaumy，A Theory of Clock Synchronization，26th Symp.on Theory of Computing，May 1994

[3] 李孝辉，杨旭海，刘娅，张慧君，施韶华.时间频率信号的精密测量.北京：科学出版社，2010

[4] F.B.Schneider，A Paradigm for Reliable Clock Synchronization.1986

[5] D.Barsotti，L.P.Nieto，A.Tiu，Verification of Clock Synchronization Algorithms：Experiments on a combination of deductive tools.2005

[6] M.Przedwojski，I.Markovsky，E.Rogers，Estimation of clock synchronization errors.IEEE SIGNAL PROCESSING LETTERS

[7] P.Ohly，D.N.Lombard，K.B.Stanton，Hardware Assisted Precision Time Protocol Design and case study

[8] 李庆扬，王能超，易大义.数值分析.北京：清华大学出版社，2001