雷达非平稳海杂波对杂波协方差矩阵和CFAR性能的影响研究

胡纪军 陈 辉 刘 婕 张 波

(1.西安计量技术研究院，西安 710068；2.户县质量技术监督局，西安 710000；3.西安电子科技大学， 西安 710000)

0 引言

为了抑制杂波和干扰的有害影响，现代雷达中采用了恒虚警、自适应阵列和空时自适应处理等诸多自适应处理技术。在雷达自适应系统中，通常采用训练数据来估计干扰协方差矩阵，在实际环境下，训练数据经常可能混有干扰目标，较强离散的杂波尖峰，还有一些其它类型的干扰，致使训练数据变成非均匀的。这种非均匀性对检测器性能的影响在很多文献中已经提及[1]。然而，另外由于杂波的非平稳特性导致的非均匀性也会严重的降低雷达性能。近来的一些对实测数据的实验揭示了海杂波是一个非平稳的过程[2-3]。本文对实测海杂波数据进行了幅度及谱分析，验证了其非平稳性，并分析了非平稳性对归一化自适应匹配滤波器(NAMF)的性能影响，对构造新的检测器提供了指导参考。

1 高分辨雷达回波模型及归一化自适应匹配滤波检测器

许多实验数据验证了在高分辨力和低入射角的情况下雷达海杂波可以看做是一个复合高斯过程[4]。在复合高斯模型当中最常采用的是Weibull分布和k分布，它们的分布模型都包括一个形状参数和一个尺度参数。已经提出的最优检测器是参考在Weibull和k杂波中的相参脉冲串且已知它们的谱特征。然而，这些检测器需要知道杂波分布的参数，而这在实际当中往往是不现实的。于是，我们对判决独立于杂波分布参数且检测门限也与杂波统计量无关的检测器比较感兴趣。文献[5]中提出的归一化匹配滤波器(NMF)对不同杂波分布(复合高斯模型)保持了恒虚警特性。于是为了构造在复合高斯杂波背景下完全自适应的检测器，我们将NMF中的杂波协方差矩阵用一个合适的估计矩阵来代替。得到的检测器称作归一化自适应匹配滤波器(NAMF)[6]。用检测单元周围距离单元的不含目标的训练数据来构造几种不同的协方差矩阵。这些协方差矩阵的估计都基于假设：所有训练数据不包含干扰和目标，并且和被测单元的数据具有同样的协方差矩阵。

在杂波环境中的雷达信号检测可以用下面的二元假设检验来表示：

(1)

在上式中r表示从基带信号采样的N维复向量接收的信号，u表示希望的目标回波，c表示被测单元的杂波。r1r2…rK表示N维的没有目标和干扰的训练数据。有用信号可以表示为u=ap，这里p表示目标的导向矢量，a是有关信道传播影响以及目标雷达截面积的未知参数。在H0假设下，回波只包含杂波数据c。当杂波的概率密度函数属于复合高斯函数族时[7]，c可以看作是两个独立的随机变量之积，如下：

(2)

这里{x,x1,…xK}是一串独立同分布复的零均值，圆对称的随机向量(又称亮斑)且具有单位功率，其协方差矩阵为正定，即x,xi∈cN(0,M)，t和ti(又称纹理)是实的非负的随机变量且独立于x和xi。

假定已知杂波的协方差矩阵M，归一化的自适应匹配滤波检测器可以如下表述：

(3)

2 协方差矩阵估计

本文引入三种协方差矩阵的估计，在后面将会用这三种协方差矩阵带入式(3)来研究检测器性能。

1)样本协方差矩阵SCM：

(4)

2)归一化的协方差矩阵NSCM[8]

(5)

3)固定点最大似然估计协方差矩阵FP[9]

(6)

3 海杂波实测数据的统计和谱分析

本文主要目的是研究式(3)检测器对前述的三种协方差矩阵构造和纹理统计量的CFAR特性。我们采用某X波段搜索雷达对海实测数据，雷达架高10m，脉冲重复频率PRF为1kHz，波速宽度0.9度。图1为一个距离单元上的不同时间的杂波幅度图。

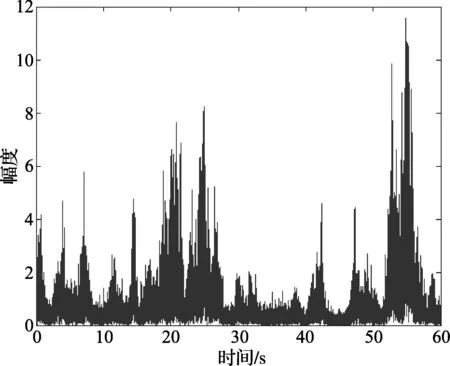
图1 一个距离单元上的杂波幅度

3.1 杂波数据的概率密度函数

通过对不同距离单元数据的分析发现，该组数据的幅度分布符合k分布，且每个距离单元的形状参数都不同。图2为一个单元的数据幅度的概率密度图，由图可见实测数据与k分布的概率密度函数吻合程度较好。图3为不同距离单元k分布的形状参数分布图，由图可见HH通道的v参数总是低于VV通道，因此可以得出HH通道的尖峰特性大于VV通道。

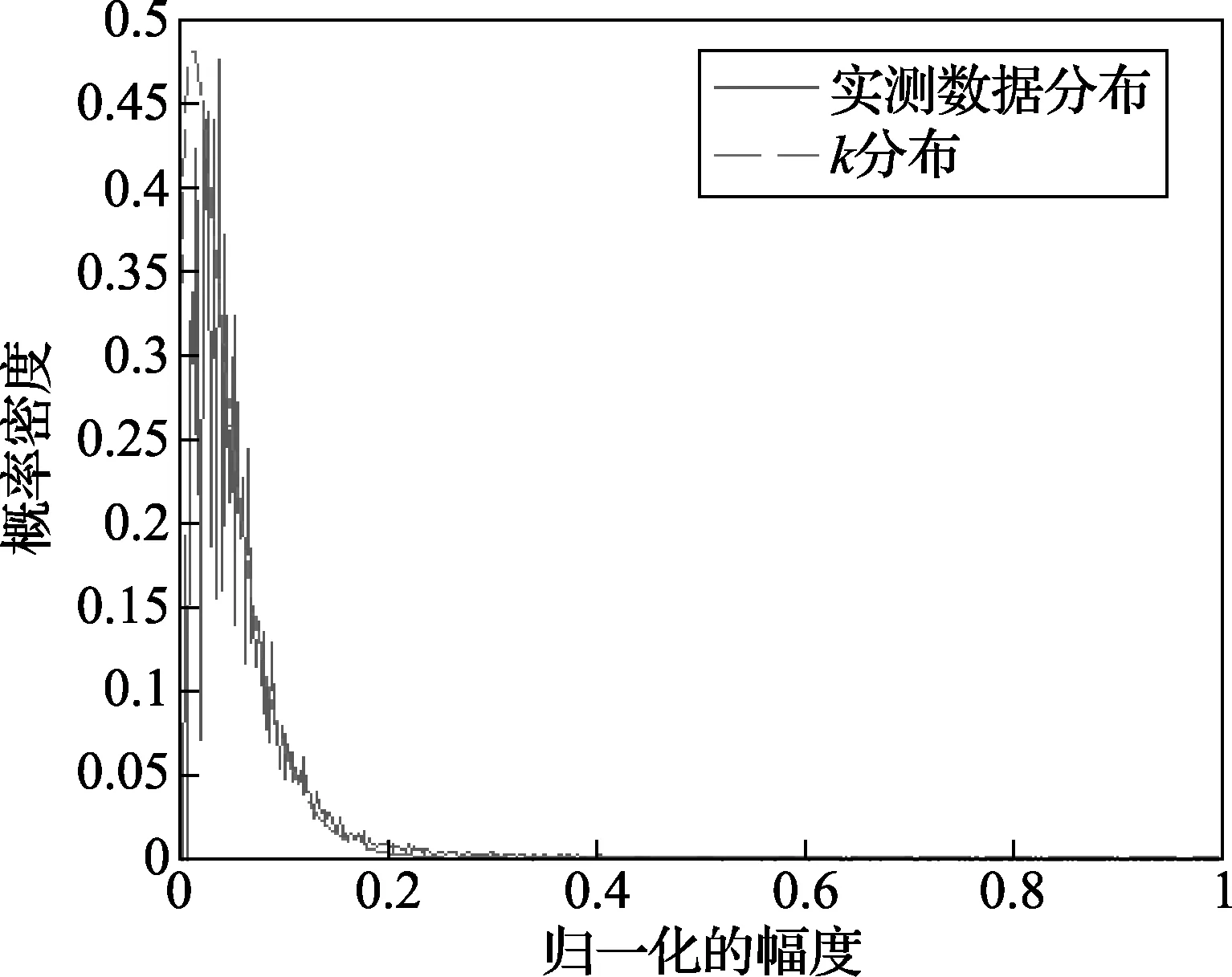
图2 一个单元的杂波幅度分布

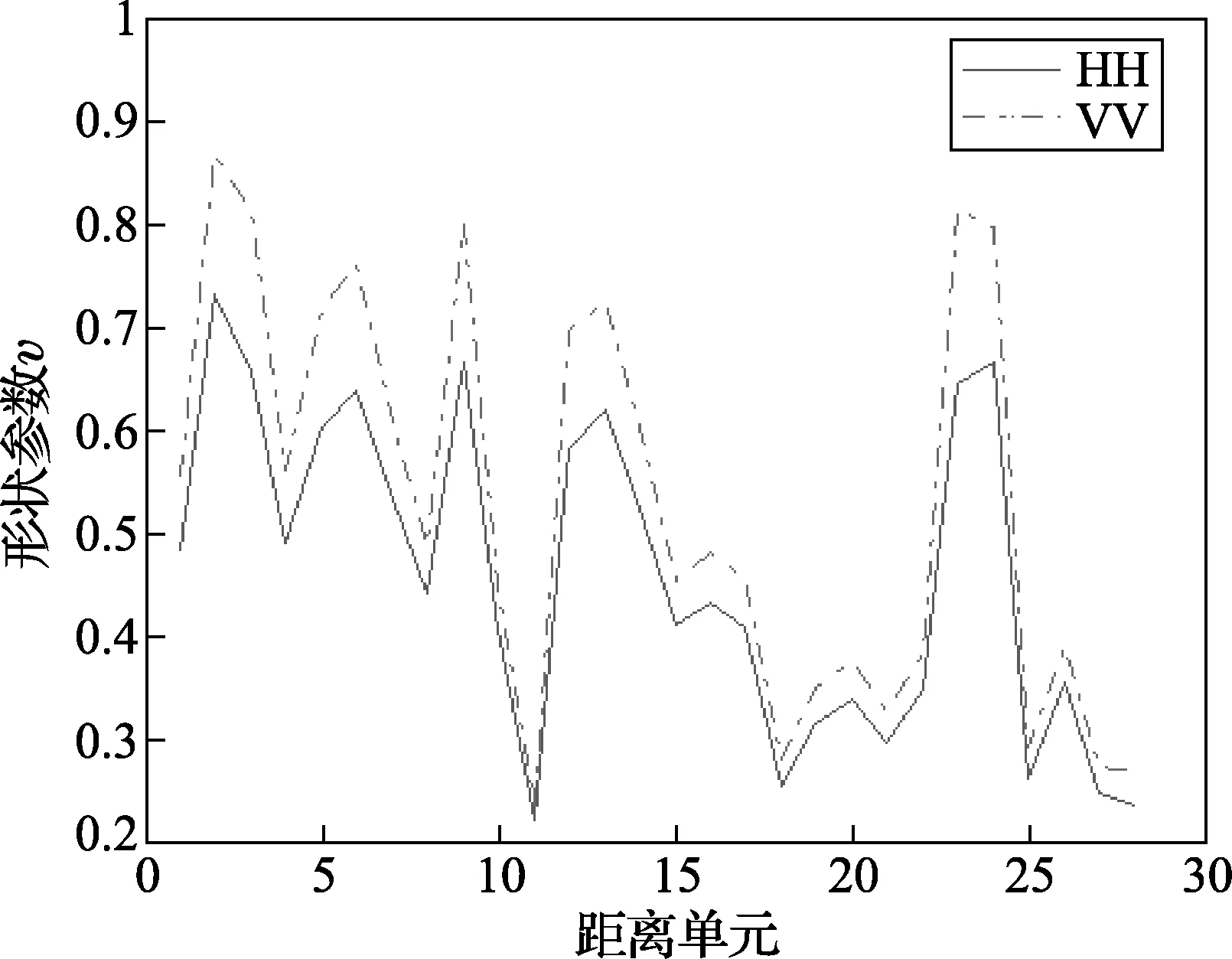
图3 不同距离单元上的形状参数

3.2 谱分析

我们对每个距离单元的数据做了功率谱(PSD)分析，对数据做加窗的welch功率谱，使用256点的矩形窗，每次滑动重叠50%的样本点。结果如图4所示，图5为一个距离单元上的功率谱图。

图4 不同距离单元上的功率谱

图5 一个距离单元上的功率谱

由图4可看到功率谱在各个距离单元上都不同，显示了杂波的空间非平稳性。PSD的峰值在150～200Hz之间。我们计算了每个距离单元的谱图，这里只显示第一个距离单元的VV通道数据的谱图，其它极化通道数据也显示了类似的特性。在图6中可以看到一些时间上周期性的特征，特别是在0～20s之间和30～40s之间，这些显示了海杂波时间上的非平稳特性。

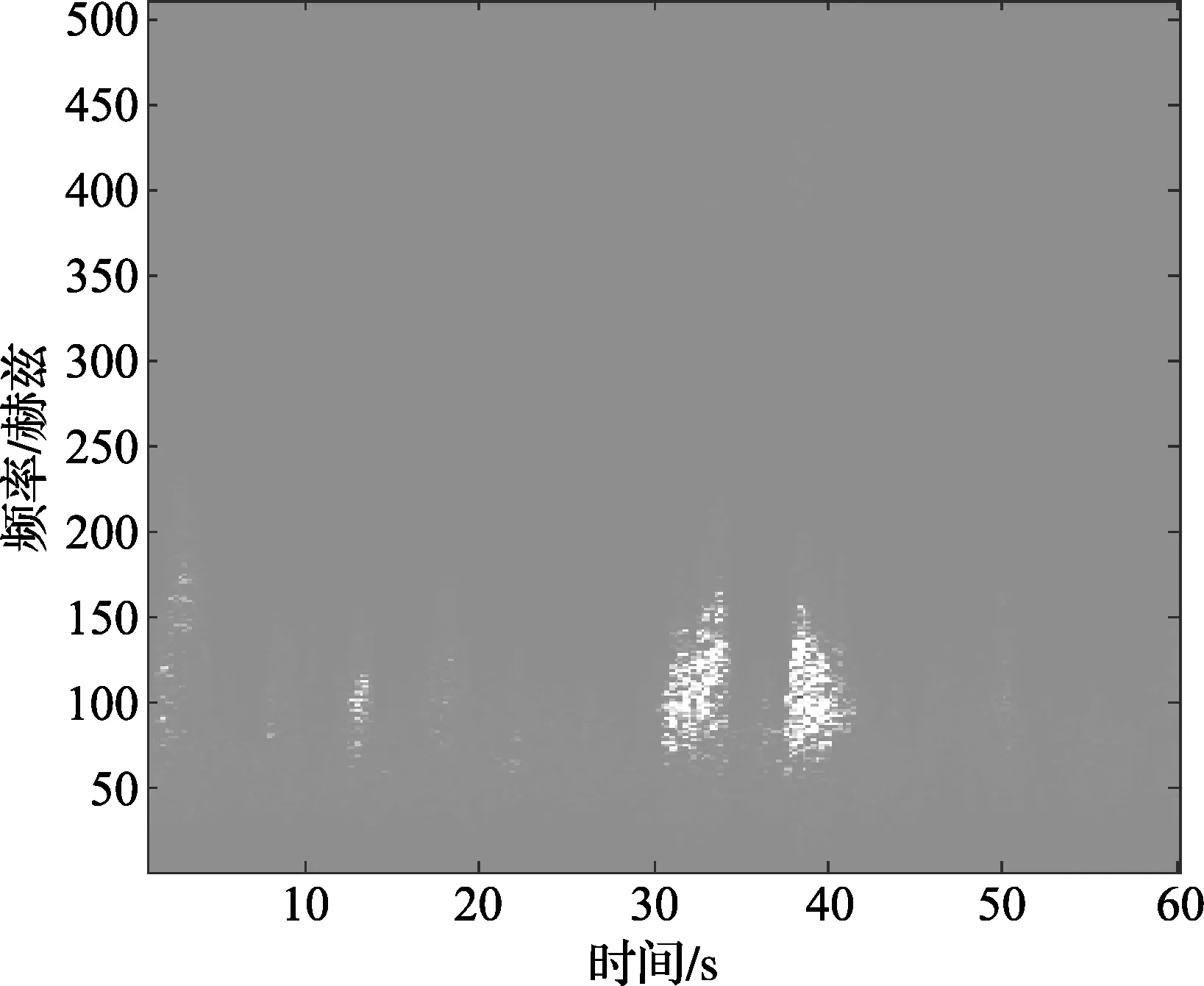
图6 一个距离单元上的频谱

4 检测器性能和恒虚警特性分析

为了评估NAMF的性能，我们采用N×(K+1)的数据窗，N为脉冲数，K为训练数据的单元数。被测单元(CUT)位于窗的中间。窗在空间上从距离单元上滑动，在时间上以重复N/2的重复数滑动，一直到数据的底端。总的实验次数就等于Ntr=2(Np-N/2)(Nc-K-1)/N，Np为脉冲数，Nc为距离单元数。为了研究检测器性能，设N=8，K=16，则导向矢量为：

p=[1,exp(j2pfd),…,exp(j2p (N-1)fd)]T

式中，fd为归一化的目标多普勒频率。为了估计系统的检测性能，在杂波数据中加入一个swerling I型起伏目标，这时被测单元的数据可以表示成

r(n)=aexp(j2pfdn)+d(n)

式中，Nc是距离单元数；m是每个单元的点数。结果如图7和图8所示，从图中可明显看出对于三种不同协方差矩阵的NAMF检测器性能，杂波的非平稳性影响了检测器的检测概率。

图7 VV通道N=8，K=16，Pfa=10-2

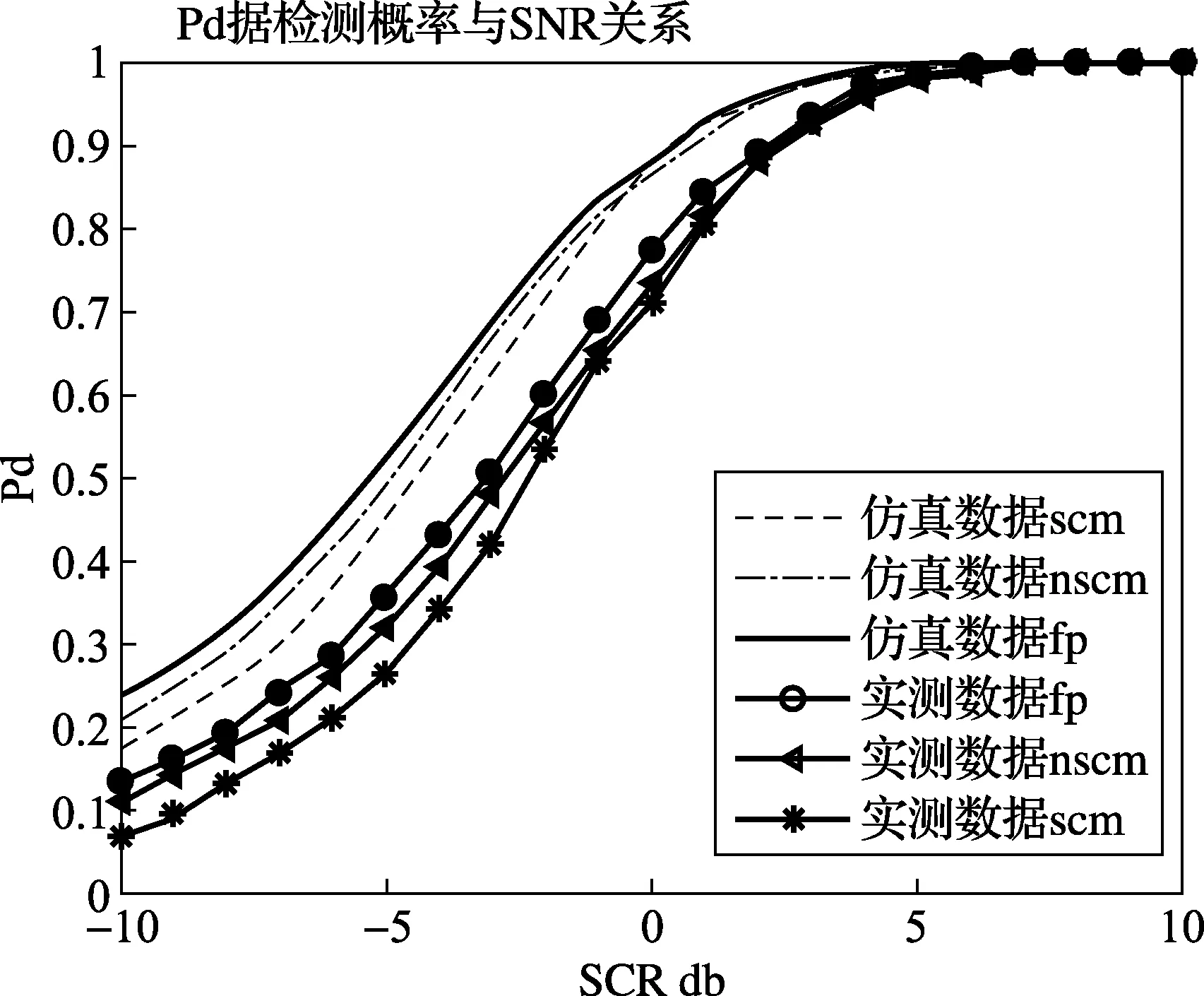
图8 HH通道N=8，K=16，Pfa=10-2

由图看出，对于采用所有三种协方差矩阵的NAMF检测器，实测数据下检测器的性能都低于采用仿真的平稳杂波数据下的性能。杂波的非平稳性影响了系统的检测概率Pd，实际的Pd总是低于对应的仿真数据下的检测概率。

5 结束语

本文分析了某X波段雷达实测海杂波数据，使用该数据检验了归一化的匹配滤波检测器的检测性能，验证了时间和空间非平稳性对检测器性能的影响。一般假定已知被测单元和训练数据单元的杂波特性，假定其在空间和时间上是平稳的，但是在实际环境下，往往海杂波是非平稳的。我们的统计分析结果如下：

1)被测海杂波显示了与k分布的很好拟合，但是每个距离单元的形状参数都不同。

2)在时间和空间上亮斑分量的PSD并不是恒定的，因此杂波在时间和空间上是非平稳的。谱图显示了在时间上PSD的某些周期性。

为了研究非平稳杂波对检测器CFAR特性的影响，我们产生了k分布杂波，它的协方差矩阵等于实测数据平均协方差阵，并且杂波的形状参数等于各单元形状参数的平均值vm。通过对仿真数据的处理，对虚警概率Pfa=10-2设置了归一化门限。然后使用实测数据对NAMF检测器的检测性能进行了测量，如果实测数据与仿真数据具有相同的特性的话，那么它们的检测性能应该很接近，但是我们的结果显示检测性能具有较大差异。这些差异大部分是因为实测数据的空间和时间的不平稳性造成的，对于一个固定的Pd这种不平稳性造成的损失大约有2～4dB。这种非平稳性的影响随着尖峰的增加和虚警概率的降低而加剧，因此构造新检测器的一个可能方向就是抑制海杂波的非平稳性以提高目标的检测概率。

[1] K.R.Gerlach，“Outlier resistant adaptive matched filtering”，IEEE Transactions on Aerospace and Electronic Systems，vol.38，no.1，pp.885-901，2002

[2] M.Greco，F.Gini and M.Rangaswamy，“Statistical analysis of measured polarimetric clutter data at different range resolutions”，IEE Proceedings，Radar，Sonar and Navigation，Vol.153，No.6，pp.473-481，December 2006

[3] Haykin S.，Bakker R.，Currie B.W.，“Uncovering Nonlinear Dynamics-The Case Study of Sea Clutter,” Proceedings of the IEEE，Vol.90,No.5 ，pp.860 -881，May 2002

[4] E.Conte，A.De Maio and G.Ricci，“Covariance matrix estimation for adaptive CFAR detection in compound-Gaussian clutter”，IEEE Transactions on Aerospace and Electronic Systems，vol.38，No.2，pp.415-426，April 2002

[5] E.Conte，M.Lops，G.Ricci，“Asymptotically optimum radar detection in compound Gaussian clutter”，IEEE Transactions on Aerospace and Electronic Systems，vol.31，no.2，pp.617-625，April 1995

[6] M.Rangaswamy，“Statistical analysis of the non-homogeneity detector for non-Gaussian interference backgrounds”，IEEE Transactions on Signal Processing，vol.53，No.6，pp.2101-2111，June 2005

[7] Rangaswamy，M.，Weiner，D.D.，and Ozturk，A.(1993)Non-Gaussian vector identification using spherically invariant random processes.IEEE Transactions on Aerospace and Electronic Systems，29，1 (Jan.1993)，111-124

[8] F.Gini，M.Greco，“Covariance matrix estimation for CFAR detection in heavy clutter”，Signal Processing，vol.82，pp.1495-1507，2002

[9] F.Pascal，Y.Chitour，J.P.Ovarlez，P.Forster and P.Larbazal,“Covariance structure maximum likelihood estimates in compound Gaussian noise：existence and algorithm analysis”，IEEE Transactions on Signal Processing，Vol.56，No.1，pp.34-48，Jan.2008