电子式互感器校验仪同相分量与正交分量的交叉影响研究*

张杰梁

(福建省计量科学研究院，福州 350003)

0 引言

随着电网技术的高速发展，电子式互感器对于电力安全、经济地运行具有越来越重要的意义,市场前景极其广阔。但从稳定性和准确性来看，电磁式互感器仍然占有一定的优势。为了确保电磁式互感器提供可靠的测量数据，必须采用有效的计量标准器具对其进行检定。从互感器的检定方法来看，由于各类间接检定方法尚未列入国家计量检定规程，所以，目前国内的计量检定机构大多采用传统比较法对各类互感器进行检定。

互感器校验仪是一种测量电压互感器和电流互感器比例误差的仪器。该仪器采用先进的电子测量技术和(或)电工测量技术，较好地解决的互感器的检定技术难题。然而，由于互感器校验仪同相分量和正交分量的交叉影响会给测量结果带来一定的误差，即同相分量和正交分量的分解难免要产生相位上的误差，所以一般的互感器校验仪只能达到2级或3级。为了确定互感器校验仪的综合误差，国家计量检定规程 JJG 169《互感器校验仪检定规程》规定，对校验仪进行首次检定时，要采用复合检定的方法，同时，对检定结果进行判断时，也应采用复合误差公式进行判断。

从测量原理上看，互感器校验仪可分为电工式和电子式两大类。考虑到早期生产的互感器校验仪一般为电工式的，这类校验仪均属于直角坐标型校验仪，而目前生产的互感器校验仪大多数为电子式的，这类校验仪有直角坐标型也有极坐标型的，鉴于此，新的互感器校验仪检定规程删去旧规程中对直角坐标式校验仪的限定，但从检定方法上看，依旧采用检定直角坐标式校验仪的方法。本文将着重分析直角坐标型电子式互感器校验仪正交分解原理，并通过试验分析互感器校验仪同相分量和正交分量的交叉影响，进一步验证JJG169《互感器校验仪检定规程》中对互感器校验仪复合误差定义的科学性[1-2]。

1 影响电子式互感器校验仪测量结果的因素分析[3-5]

与传统的电工式互感器检验仪相比，电子式互感器校验仪可较好地解决负载效应、自动控制等问题，同时该类仪器操作简单、测量范围宽、检定速度快且容易实现产品的小型化。但由于该类仪器具备同时显示同相分量和正交分量的示值，同相分量和正交分量的分解必然给测量结果带来一定的误差。此外，目前国内广泛应用的电子式互感器校验仪大多采用阻容移相电路来实现互感器误差数据的测量。由于这类电路中积分放大器的增益是信号频率的函数，所以，若在使用时的信号频率与检定时的频率不同，将会给检定结果带来一定的附加误差。

以上影响电子式互感器校验仪测量结果的两个主要因素中，频率误差可通过JJG 169—2010 《互感器校验仪检定规程》中规定的附加误差修正来减小其影响。因此，减小同相分量和正交分量的交叉影响是提高电子式互感器校验仪准确度等级的主要手段。为了分析电子式互感器校验仪同相分量和正交分量的交叉影响，现给出两个分量的向量图，如图1所示。

图中X0与Y0分别表示被测电子式互感器校验同相分量与正交分量的实际值。X1与Y1表示电子式互感器校验仪测量时所获得的两个示值，其中，X1为同相分量，Y1为正交分量。由于电子式互感器校验仪的两个分量的测得值均存在相位误差，假设X1的相位误差为a，Y1的相位误差为β，则电子式互感器校验仪工作时，这两个相位误差必然会给同相分量和正交分量实测值产生一定的影响，即X1的相位误差a要产生一个ΔY分量，ΔY将会叠加到Y1中去，使其显示值改变为Y2=Y1+ΔY；同理，Y1的相位误差β要产生一个ΔX分量，ΔX将会叠加到X1中去，使其显示值改变为X2=X1+ΔX。由此可见，具有两个测量示值的仪器，只要这个分量是共处在一个直角坐标的测量系统之中，则每个分量的相位误差必然要对另一个分量的示值产生一个叠加误差。

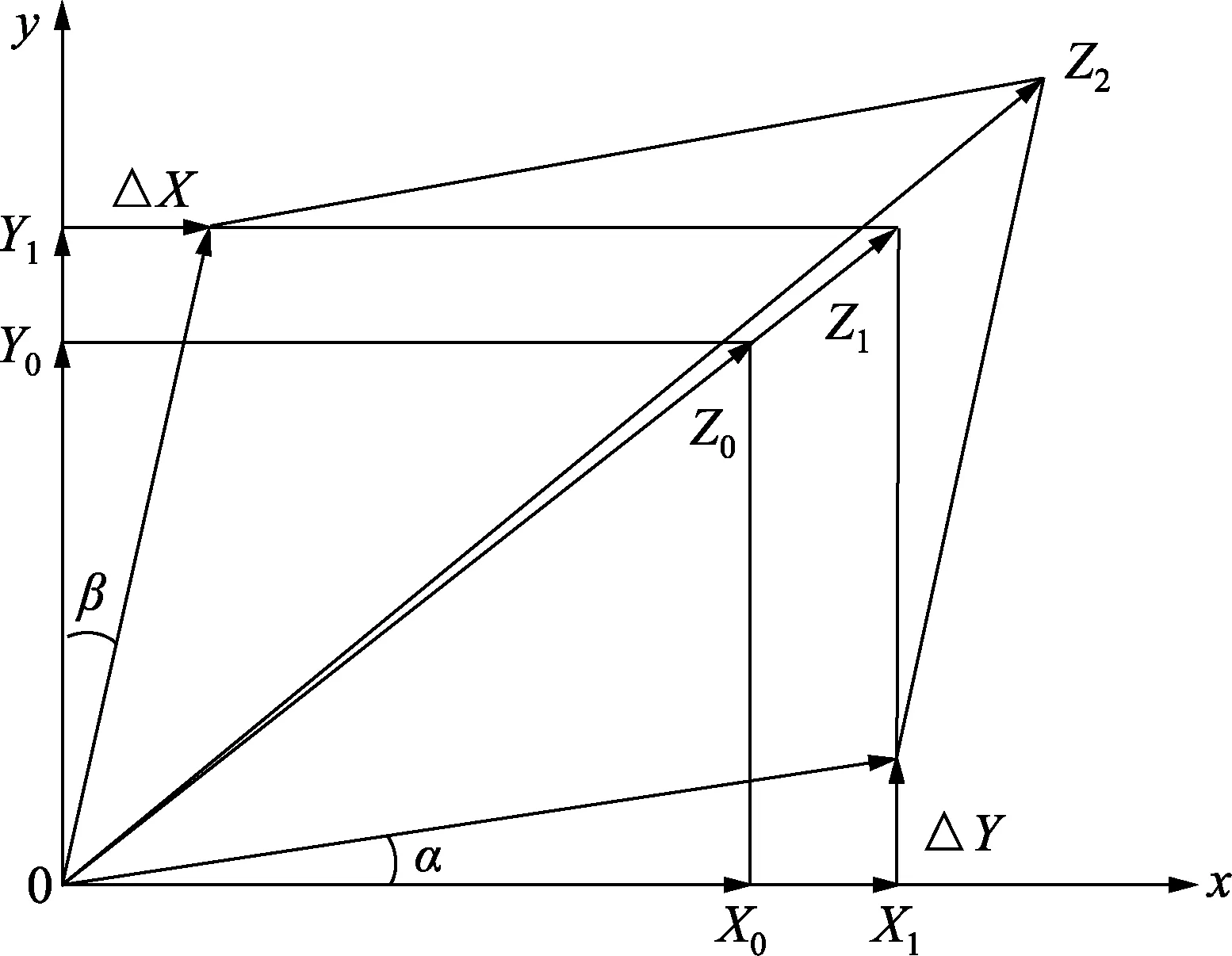
图1 同相分量与正交分量的交叉影响示意图

2 同相分量与正交分量的交叉影响试验

为了确定电子式互感器校验仪两个分量交叉影响给检定结果带来的误差，现以早期生产的HEW2002型和近几年改进的HN-2K01B4型互感器校验仪为例，对其电流互感器测量回路同相分量和正交分量的相互影响进行进行试验，试验结果如表1～表4所示。

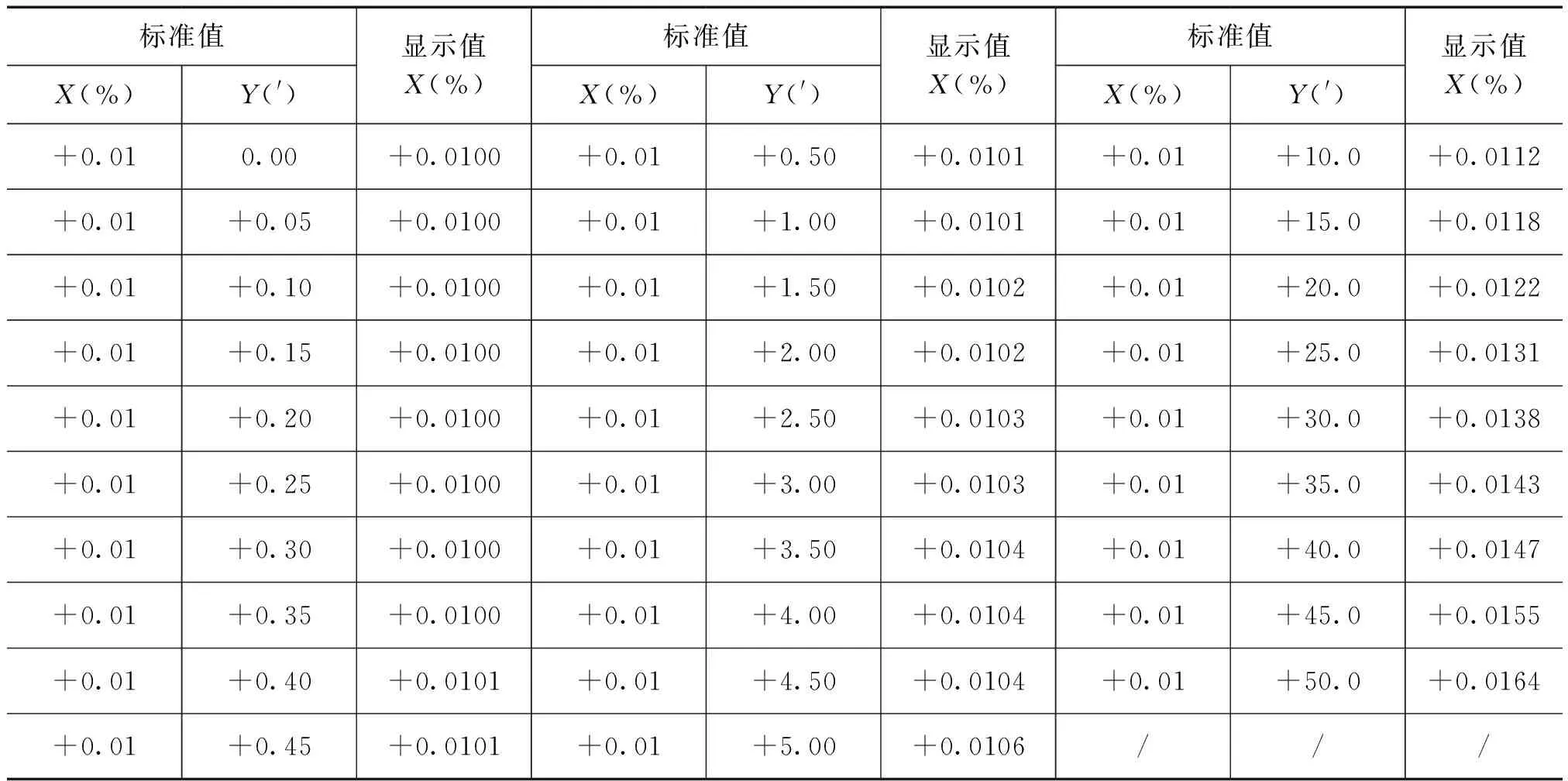
表1HN-2K01B4型互感器校验仪正交分量对同相分量影响的试验数据

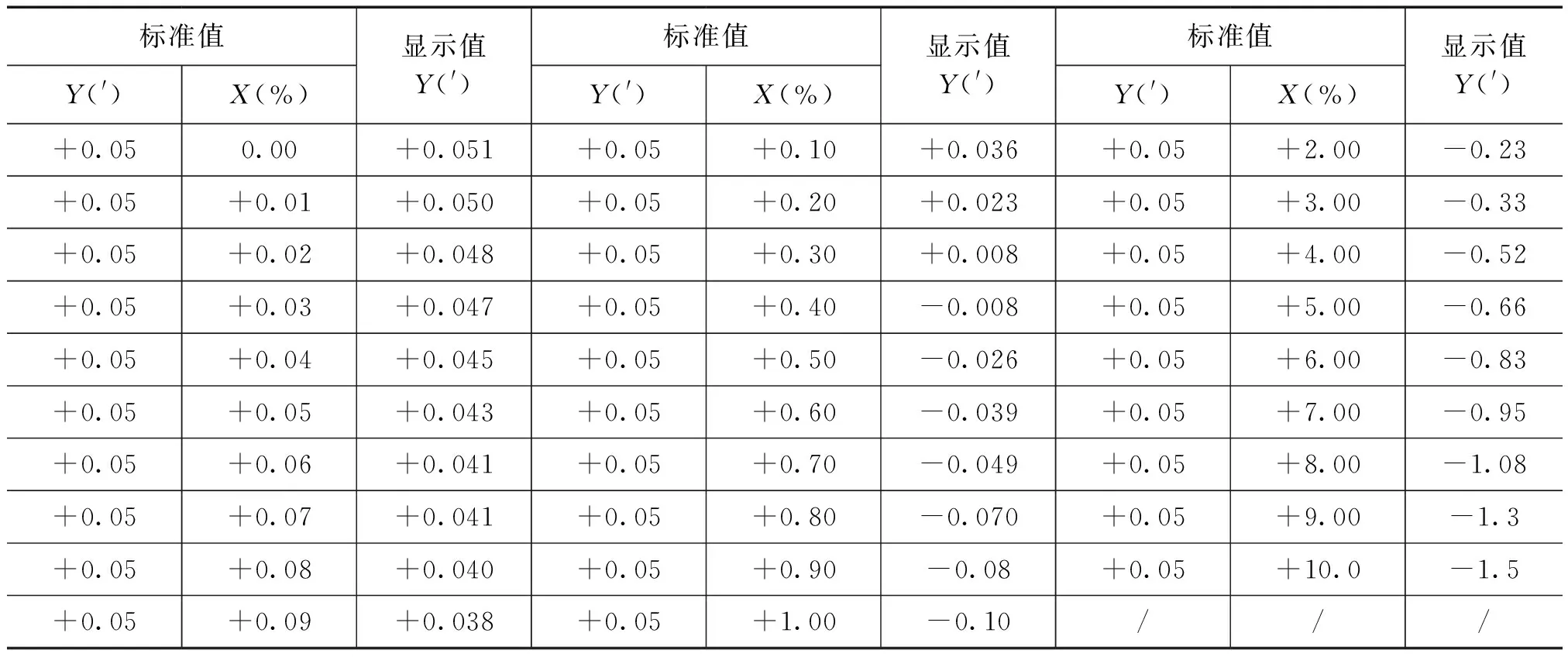
表2HN-2K01B4型互感器校验仪同相分量对正交分量影响的试验数据

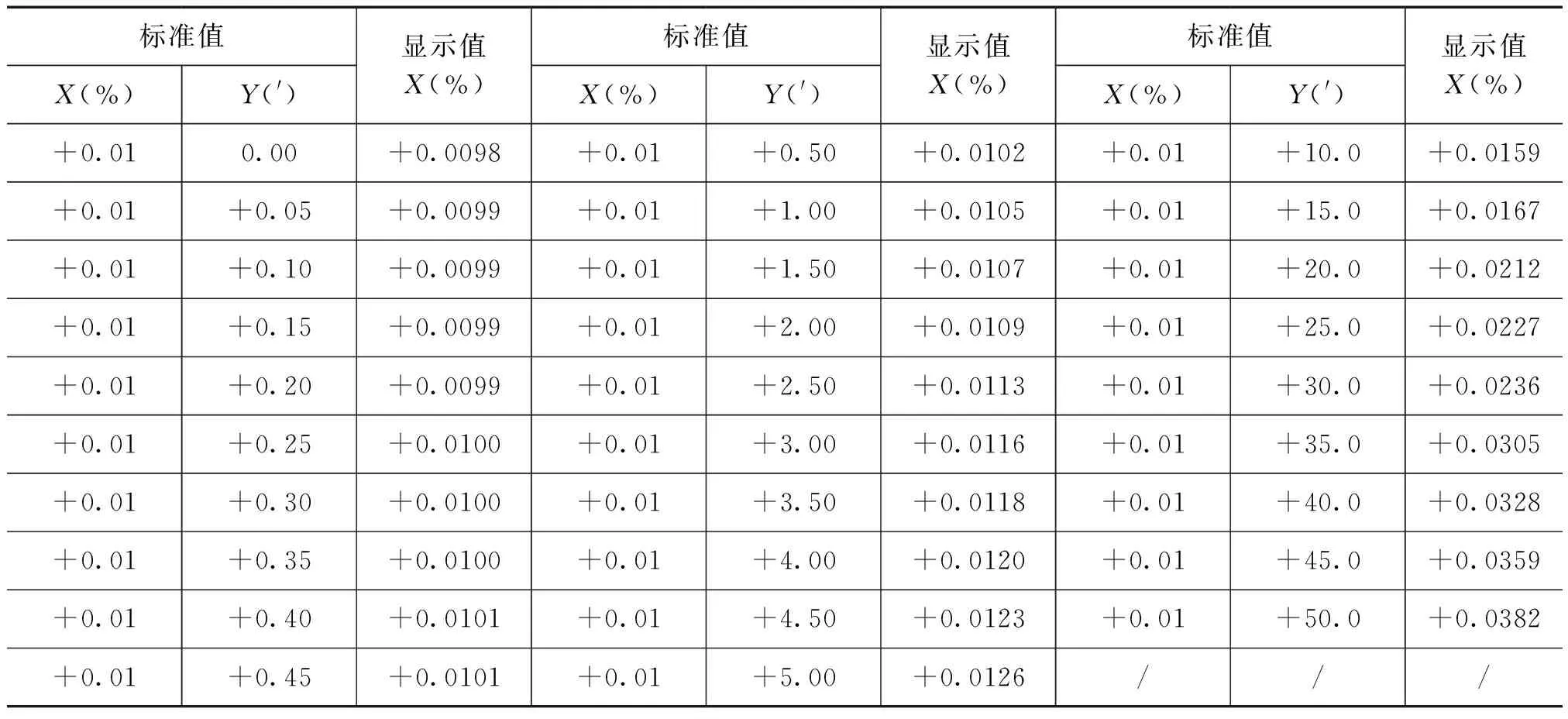
表3HEW2002型互感器校验仪正交分量对同相分量影响的试验数据

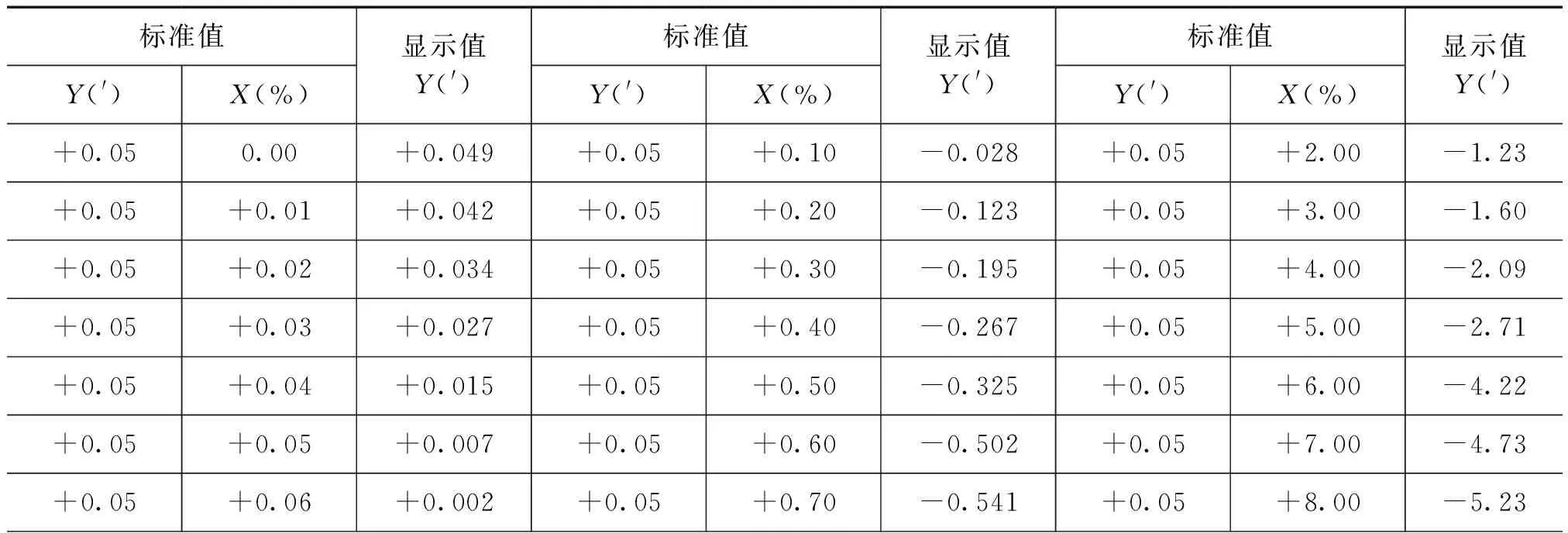
表4HEW2002型互感器校验仪同相分量对正交分量影响的试验数据

续表

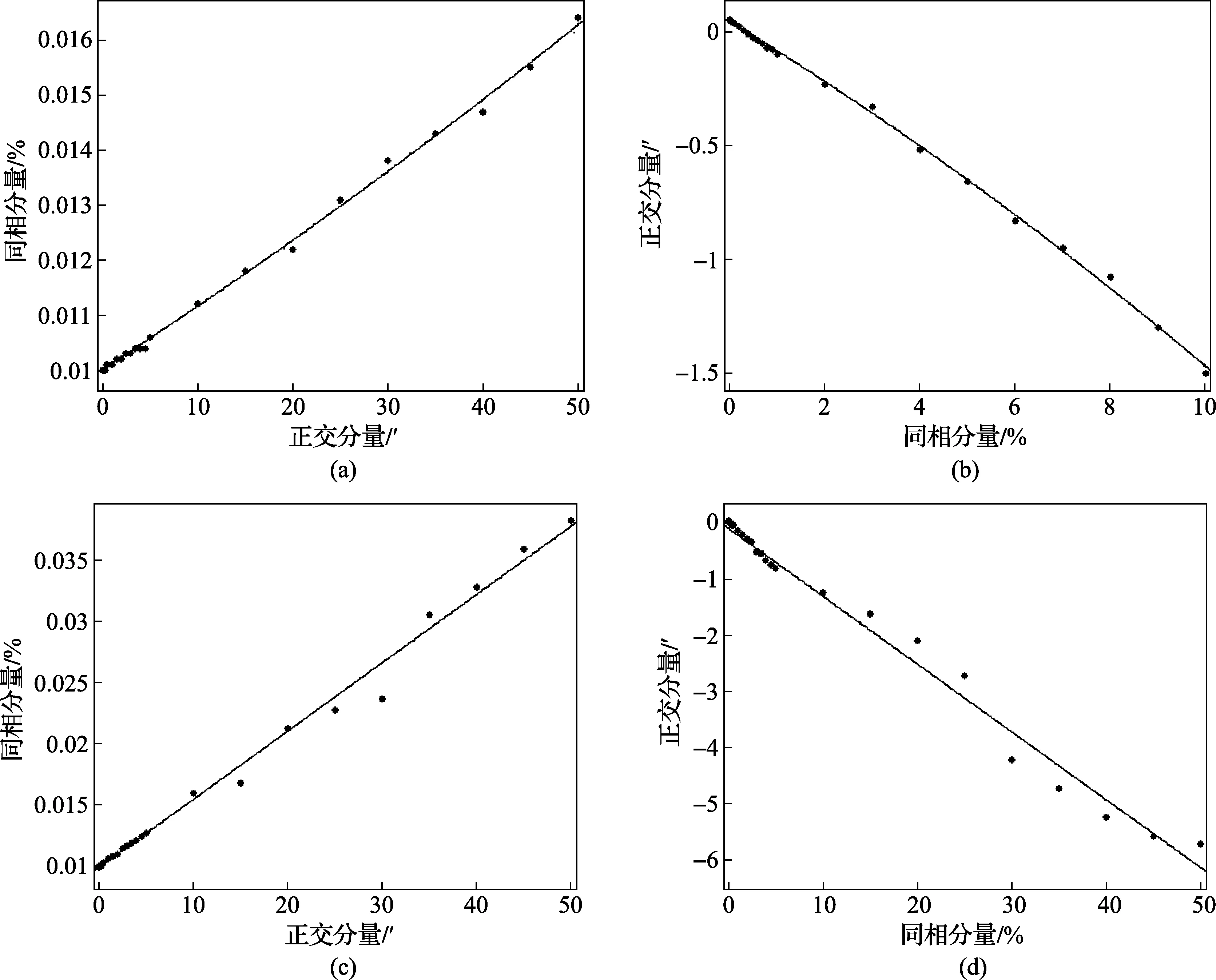
图2 电子式校验仪频率特性拟合曲线

为了分析电子式互感器校验仪同相分量与正交分量的交叉影响，现采用MATLAB曲线拟合工具箱对表1～表4的测量数据进行二次多项式曲线拟合，拟合曲线分别如图2所示。从图中可以看出，当正交分量增大时，相同分量也逐渐增加；增大同相分量时，正交分量逐渐变小，并向负方向变化。当X与Y两个分量大小相差较大时，示值较大者的相位差对示值较小者的迭加误差尤为严重。需要进一步指出的是，虽然两种型号的互感器校验仪均符合JJG 169—2010《互感器校验仪检定规程》2级要求，但前者的交叉影响量相对较小，据该公司研制者介绍，该款校验仪在原有正交分解技术的基础上，对测量电路的采样部分进行改造，从而在一定程度改善了两个分量的交叉影响。鉴于同相分量与正交分量交叉影响带来的误差无法避免，故JJG 169—2010《互感器校验仪检定规程》采用复合误差的公式来定义电子式互感器校验的基本误差量限：

ΔX=±K(X·a%+Y·a%+DX)

(1)

ΔY=±K(X·a%+Y·a%+DY)

(2)

式中，ΔX为同相分量示值误差限值；ΔY为正交分量示值误差限值；K为仪器的量程系数；X为同相分量示值的绝对值；Y为正交分量示值的绝对值；DX为同相分量示值中的最小分度值或量化值；DY为正交分量中的最小分度值或量化值；a为仪器的准确度级别指数。

3 同相分量与正交分量交叉影响的改善[6-9]

传统的电子式互感器校验仪一般采用阻容移相原理来进行正交分解，其积分电路如图3所示。

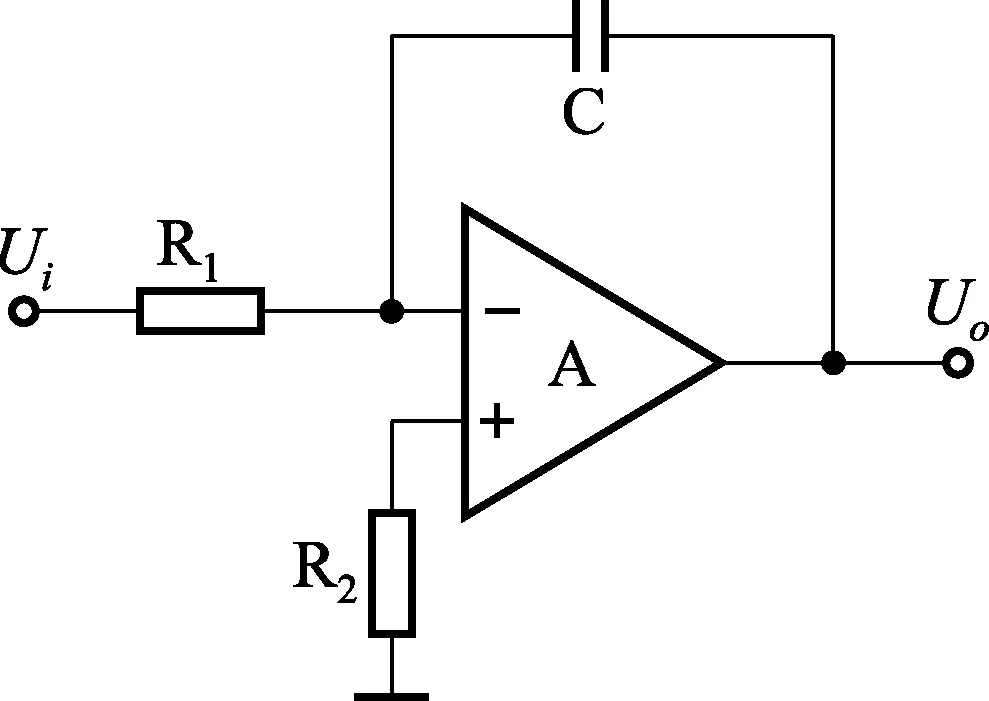
图3 90°移相所采用的积分电路

图3中，A为运算放大器，C为积分电容，R1为积分电阻，R2为平衡电阻，输入输出信号分别为Ui和Uo，传递函数为：

(3)

式中，t为积分放大器的时间常数。由式3可知，积分放大器的增益是电源频率的函数。若校验仪在使用时的信号频率与检定时信号频率不同，将会给检定结果带来一定的附加误差。为此有必要采用基准正交分离电路来实现正交移相。基准正交分离电路中，同相分量和正交分量的相位误差不会因为频率的改变而产生附加误差。

基于基准正交分离电路电子式互感器校验仪的原理框图如图4所示。图中，AGC为自动增益控制电路，a与β为基准正交分离电路的输出驱动信号，Um为参考信号，a与β的相位关系以及它们与Um的相位关系与工作频率无关。由于基准正交分离电路是一种逻辑电路，其相位误差主要取决于逻辑脉冲的前沿与后沿特性，故只要相应元件的时间响应速度够快，就会使这项误差得到改善。其次，这种四分频移相技术是理论性质的移相，只要电路连接正确，产生的同相与正交驱动信号就能保证相移为准确的90°，不需要任何调整，也不会随着时间的推移发生变化。

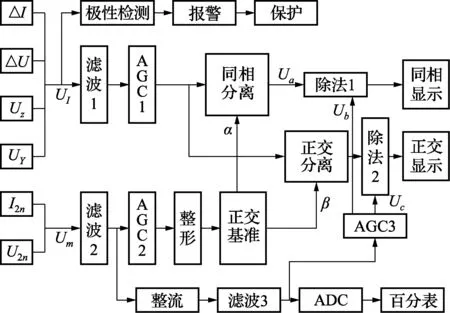
图4 基于基准正交分离电路电子式互感器校验仪的原理框图

4 结束语

本文在分析电子式互感器校验仪正交分解原理的基础上，通过复合检定方法对HN-2K01B4型和HEW2002型电子式互感器校验仪的两个分量的交叉影响进行试验，试验结果表明，当正交分量增大时，同相分量也逐渐增加；增大同相分量时，正交分量逐渐变小，并向负方向变化。当X与Y两个分量大小相差较大时，示值较大者的相位差对示值较小者的迭加误差尤为严重。为了提高电子式互感器校验仪的准确度等级减小其同相分量和正交分量的交叉影响，文中介绍了一种基于正交分离电路的电子式互感器校验仪，该原理的电子式互感器校验仪在很大程度上减小了两个分量交叉影响和工作频率对测量结果的影响，提高了仪器的准确度等级。

[1] 国家质量监督检验检疫总局.JJG 169—2010 互感器校验仪检定规程[S].北京：中国计量出版社，2010

[2] 张杰梁，黄洪，方杰．电流互感器负荷箱的检测及误差分析[J]．计量技术，2010(12)

[3] 刘庆余．互感器校验仪整体检定的述评(上)[J]．电测与仪表，2003，40(447)

[4] 刘庆余．互感器校验仪整体检定的述评(下)[J]．电测与仪表，2003，40(438)

[5] 张杰梁．电流互感器现场测试仪校准方法研究[D]．厦门大学，2011

[6] 李童杰，张晓更．基于DSP的电子式电流互感器校验仪的研制[J]．仪器仪表学报，2008(8)

[7] 刘庆余．互感器校验仪的原理与整体检定[M]．北京：中国计量出版社，2003

[8] 张庆．电子式互感器模/数转换电路的设计与应用[J].低压电器，2009(14)

[9] 车现伟，王晓东，樊永华，等．同相分离法在精密电流互感器校验仪中应用的研究[J]．计量技术，2010(12)