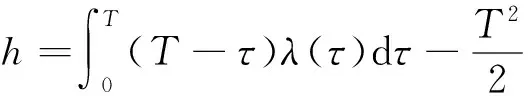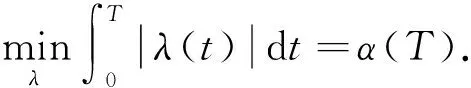变分不等式的应用
杨允利
(陕西省蓝田县教师进修学校, 陕西西安 710500)
1 序言
变分不等式起源于数学物理问题和非线性规划问题。20世纪60年代中期,在非线性规划的研究中出现了线性和非线性互补问题,它们进一步发展成了有限维空间中的变分不等式。20世纪70年代以来,作为现代偏微分方程理论的重要部分的变分不等式理论得到深入发展,至今已经较为成熟[1]。
变分不等式在现实生活中有着非常重要和直观的意义。在一般的工程技术领域、高新技术领域、科研探索以及日常生产和现实生活中,有些复杂问题,往往给人以变幻莫测的感觉,难以掌握其中的奥妙[2]。 随着科学技术的飞速发展及信息时代的到来,有着十分抽象形式和严格逻辑体系且来源于实际需要的各种模型,对培养人的素质、数学思维能力和进行数值计算能力方面具有不可替代的作用,变分不等式就是其中非常重要的一例[3]。
2 变分不等式的定义以及它的一些性质
对于u∈M,我们来考虑最小值问题:F(u)=min!, 并且对于所有的v∈M和给定的u∈M,伴随着变分不等式:δF(u;v-u)≥0, 对应到对于所有v∈M和给定的u∈M,〈F′(u),v-u〉≥0. 我们假设:
(H1)M是实自反巴拿赫空间X的非空的、闭的凸子集。

(H3) 如果M是无界的,那么F就是弱强制的。
定理 假设(H1)到(H3)成立,那么下述成立:
(i)最小值问题F(u)=min!有解u,如果F是严格凸的,那么这个解是唯一的。
(ii)如果对所有v∈M和所有h∈X,一次变分δF(v;h)都存在,那么最小值问题F(u)=min!和变分不等式δF(u;v-u)≥0是等效的。
(iii)如果对所有的v∈M,导数F′(v)存在,那么最小值问题F(u)=min!和变分不等式〈F′(u);v-u〉≥0是等效的。
证明:(ii)定义φ(t):=F(u+t(v-u)).
如果u是最小值问题F(u)=min!的解,那么对所有t∈[0,1],φ(t)≥φ(0). 因此,
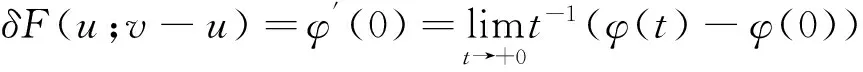
反过来,让u是变分不等式δF(u;v-u)≥0的解。那么,φ′(0)≥0,因此,φ在[0,1]上是凸的,导数φ′在[0,1]上是单调的。由均值定理可知,存在0<θ<1,使得
φ(1)-φ(0)=φ′(θ)≥φ(0)≥0.
因此,对任意v∈M,F(v)-F(u)≥0.就是说,u是最小值问题F(u)=min!的一个解[4].
3 变分不等式的应用——火箭最优控制
我们要研究一个垂直上升的火箭到达某一给定高度h并且消耗最少燃料的方案。火箭的运动方程x=x(t)由下式确定:
mx″(t)=λ(t)-mg,0 x(0)=x′(0)=0,x(T)=h, 其中,m表示火箭的质量,mg表示重力,λ(t)表示火箭的自身动力。我们忽略了消耗燃料的质量。为了简化表示方法,我们选择物理单位m=g=1. (a) 对于给定的高度h和固定的最终时间T>0,我们寻找一个解决方案F,这个方案是最小值问题min‖F‖=α(T),F∈C[0,T]*的解, (b) 我们用式子α(T)=min!决定最终时间T, [参 考 文 献] [1] ABRAHAM R, MARSDEM J, RATIU T. Manifolds, TensorAnalysis, and Applications[M]. Addison-Wesley, Reading, MA, 1983. [2] AMANN H. Ordinary Differential Equations:An Introduction to No nonlinear Analysis[M]. De Gruyter, Berlin, 1990. [3] BAGGER L. Functional Analysis[M]. A Primer.Marcel Dekker, New York, 1992. [4] COLLINS J. Renormalization[M]. Cambridge University Press, Cambridge, UK, 1984.