基于ARIMA模型的股票行情预测

李秀琴，梁满发

李秀琴/中山火炬职业技术学院公共课部讲师，硕士（广东中山528437)；梁满发/华南理工大学理学院副教授，硕士（广东广州510640)。

股市行情预测方法研究是投资人或金融投资研究者的难题，时间序列模型是一种重要的现代统计分析方法，ARIMA模型就是一种重要的时间序列模型[1]。虽然股市行情数据貌似杂乱无章，但大量文献实证研究表明，常常在某一时期市场行情模式也会反复重现，这正是ARIMA模型的应用前提条件，因此探索ARIMA模型在股票投资预测方面应用是可行的，有价值的。

时间序列分析是决策、预测的主要方法，SAS软件提供了强大的时间序列分析功能，即ARIMA（）过程[2]。模型表达形式为 ARIMA（p，d，q），其中 p 为自回归项数，q 为移动平均项数，d表示差分的阶数。若时间序列是平稳的可直接运用ARIMA模型，若时间序列是不平稳的，则需要经过d阶差分，将非平稳的时间序列转化为平稳的时间序列[3]。ARIMA模型数学表达式如下：ø（B）·Δdpt=θ（B）·εt。 式中 ø（B）是自回归算子 ， △=1-B是差分算子 ， ø（B）为移动平均算子[4]。

本文主要通过应用ARIMA时间序列模型对上证指数进行模型识别，模型拟合及检验，并运用拟合模型预测上证指数短期的走势，对预测误差分析检验，判断模型的可靠性及预测效果。

一、实证和预测

（一）数据

1.样本数据。本文数据来源于Wind资讯金融终端，选取上证指数2005年4月1日至2006年3月31日一年间的日-收盘指数作为预测模型的建模输入数据。本文将用ARIAM模型预测2006年4月份的收盘指数。

2.数据处理。本文以日-收盘指数作为预测模型的输入数据，即时间间隔的单位按日计算，这样会出现缺值。本文采用了较普遍的线性插值法，若某一天缺值，则以前一天和后一天的收盘指数相加，再除以2得出那天的值。连续多天缺值也按这种方法插值。经处理后的时间序列共有261个数据，是从2005年4月1日至2006年3月31日，部分样本如表1所示。

表1 时间序列部分样本的数据

（二）建模过程

1.数据导入。运行Enterprise Guide 3.0，打开储存在Excel中的数据，并转换成SAS的数据格式。原来的数据的日期表示形式为：年年月月日日（YYMMDD）。但在转换时，SAS软件默认的读取输入格式为：MMDDYY。因此要更改日期显示方法，生成SAS数据格式的过程为，日线（2005年4月-2006年3月）（sheet1$）→导入数据→SASUSER.1，运行后生成SAS格式的数据文件。

2.建模过程。利用上述生成的SAS数据文件，作为输入数据，创建时间序列分析及预测模型--ARIMA模型。SAS的“ARIMA建模和预测”任务分为三个阶段：认别阶段、估计阶段和预测阶段。在此之前先要对该模型设置“任务角色”，把“收盘指数”设为时间序列变量，把“日期”设为时间ID变量。

（1）识别阶段。在此阶段首先要设置的是“差分滞后”，这是模型中较为重要的参数之一。若时间序列是平稳的，那么就不需要进行差分，但本文所研究的时间序为非平稳的，因此对时间序列要进行两次一步滞后的差分即在差分滞后中填上 （1，1），这时序列的自相关和偏相关函数都呈缓慢的收敛，时间序列经过差分后，近似平稳，数据的个数由261个变为259个。

下一个要设置的就是平隐性检验及图形和结果，图形和结果主要设置自相关图形的滞后个数，以及图形显示和储存问题。

（2）参数估计阶段。选取了“执行估计步骤”后，就要设置模型定义，也是就该模型的核心内容，需要设置“自回归p（AR模型因子）”以及另一参数“移动平均Vq（MA模型因子）”。这里p和q的选取比较复杂，除了会互相影响t率外，根据文献[1]亦受 AIC准则要求限制，AIC的值越小越好。 例如选了 1至 7作为 q值， MA1，1、MA1，2、MA1，3和MA1，4 参数的 t Value分别为-0.01、0.91、-0.10 和-1.07，由于t率太小，所以该项q的假设检验并不显著，故可以丢弃这几项。

在不断调试后，得出了一个比较合理的p和q的值:P=24，26 ；q=9，10，19，22，30。 下一步就是模型选项，本文使用的是“无条件最小二乘法”。

（3）预测阶段。首先选取了“执行预测步骤”，在“观测间的时间”选项中选择“每日，不计周末”，以及确定“要预测的时间间隔”为“20”，即要预测06年4月份的收盘指数。“置信水平”定为95%，最后在图形和结果介面中勾取“预测数据”以及“实际值和向前一步预测值”。至此，模型参数设置完成！

(三)预测结果

建模完成的过程图为：日线（2005年4月-2006年3月）（sheet1$）→导入数据→SASUSER.1→ARIMA

运行结果显示：AIC的值为 2254.895，SBS的值为2283.35，两者的值也不算太大，说明模型拟合可以接受。通过ARIMA建模和预测得到的收盘指数与模型预测的将来值如图1所示。

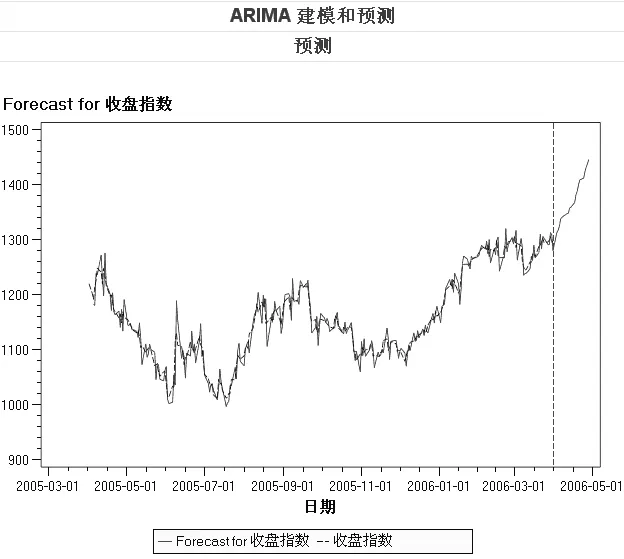
图1 收盘指数及模型预测的将来值

二、模型的预测能力评估

模型预测了06年4月3日至4月28日的上证指数收盘指数，使用Enterprise的图形工具，现将它与实际的收盘指数作比较，通过如下过程：实际指数与预测指数→导入数据→SASUSER.1→线图→HTML-线图，得到如图2所示。由此反映出模型的实际预测能力，以及预测模型在股票分析中的存在价值。

图2 上证指数收盘指数的预测指数与真实指数

从图2中能看出，预测指数虽然与真实指数在一定的差别，但已经能够很好地预测出上证指数收盘指数的基本走势，当中更有部分数值几乎与真实价相同了。

以下将参考文献[5]方法，列表计算对预测与实际值之间的误差，相对误差，如表2所示。

其中：误差＝收盘指数－预测指数；相对误差＝误差／收盘指数*100%

从表2中看出，相对误差全部都少于2%，拟合程度非常高，进一步确认了ARIMA模型在短期预测中的准确性。

表2 误差分析

三、结论

本文选取上证收盘指数作为研究对象，使用SAS软件操作了ARIMA模型建立过程，并借此来探寻股市的预测方法。本文通过ARIMA模型各种搭配反复试算，建立精度较理想的预测模型，提供了能进行股票指数短期预测的量化投资方法。由于我们选取的数据不够充分，实证结果还存在局限性，结果仅作投资参考。

[1]王波，张凤玲.神经网络与时间序列模型在股票预测中的比较[J].武汉理工大学学报（信息与管理工程版），2005， 27（6）：69-73

[2]贾勇宁.分析、预测方法在决策支持中的应用[J].铁路通信信号，2004，40（5）：12-14

[3]厉雨静，程宗毛.时间序列模型在股票价格预测中的应用[J].商场现代化，2011，(33)：61-63

[4]赵志峰.对建立中国股票价格指数时间序列模型的探讨[J].统计与信息论坛，2003，18（1）：66-69

[5]李民，邹捷中，李俊平，梁建武.用ARMA模型预测深沪股市[J].长沙铁道学院学报，2002， 18（1）：81-87