考虑时间效应的矩阵分解技术在推荐系统中的应用

段华杰

0 引言

随着电子商务规模的不断扩大，产品个数和种类的快速增长，顾客需要花费大量的时间才能找到自己想要的产品。这种浏览大量无关的信息和产品过程，无疑会降低顾客的用户体验。为了解决这些问题，个性化推荐系统应用而生。

个性化推荐系统是建立在海量数据挖掘基础上的一种高级商务智能平台，以帮距电子商务网站为其顾客购物提供完全个性化的决策支持和信息服务。个性化推荐根据用户的兴趣特点和购买行为，向用户推荐用户感兴趣的信息和产品。

1 推荐系统策略

从广义上说，推荐系统基于以下两种策略[1]:

(1)基于内容的过滤(content-based filtering)策略。该方法为每个用户或产品创建特征集来标记他们的特性。例如，一部电影的特征集可以包括电影的类型(爱情片、动作片、喜剧片、科幻片等)、导演、主演人员等。用户的特征集包括性别、年龄、个人喜好、出生地点等。推荐系统根据这些特征集为每位用户推荐匹配的产品。基于内容的策略要求系统收集额外的产品信息和用户信息，而用户信息往往不易获得，即使能够获得，也不一定真实，因此具有很大的局限性。

(2)协同过滤(collaborative filtering)策略。协同过滤(CF)策略不需要事先获得产品或用户的特征集，而仅依赖于用户过去的行为(用户对产品的历史购买情况、对产品的显式评分或隐式评分等)。协同过滤方法通过分析已经收集到的用户-产品对的评分情况猜测未知的用户-产品对的关联性，从而给出个性化推荐。

协同过滤策略存在多种实现方式，其中邻居模型（kNN）和潜在因子模型是两大主要实现方法。邻居模型又可以分为基于用户的(user-based)邻居模型和基于产品的(item-based)邻居模型。在基于用户的kNN模型中，用户对产品的评价预测是基于与此用户相似的用户所给予的评分实现的。而两个用户的相似度可以通过他们对共同的产品的评价相似度获得。

潜在因子模型（latent factor model）基于如下的假设:每个用户与每件产品都可以由若干个特征因子描述，用户与产品之间的联系能够通过两组特征因子之间的相互作用产生。当一个用户的特征刚好符合某件产品的特征时，我们认为该用户会对产品给予很高的评分，反之亦然。

2 矩阵分解模型

最近几年，一些很成功的潜在因子模型的实现方式，都是基于矩阵分解（Matrix Factorization）模型的。矩阵分解模型中，每一件产品对应一个K维的向量，每一个用户同样对应一个K维向量。产品与用户之间的关系能够通过两组向量的相关程度获得。矩阵分解模型具有很好的可扩展性和预测精度，因此能够很好的应用于现实产品推荐中。

产品推荐系统的运作是依赖于用户提供的反馈信息的。反馈信息一般分为两种:隐式反馈信息（如用户的购买记录、浏览记录、鼠标点击情况等）和显式反馈信息（如用户对产品的评分情况）。矩阵分解模型则能够很好地结合隐式和显式反馈信息。本文中仅考虑显式反馈信息。

2.1 基本矩阵分解模型（MF）

在基本矩阵分解模型中，每个用户对应一个向量，每件产品也对应一个向量，假定K为向量的维数，同时也是潜在因子的个数。那么第u个用户对第i件产品的评分预测可以表示为公式（1）

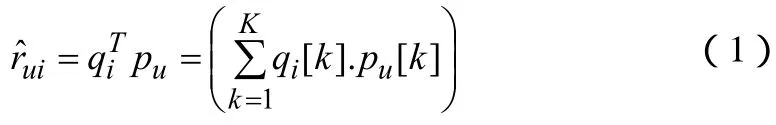
为了学习这些参数（和），我们可以通过最小化预测评分在验证集上的均方误差公式（2）

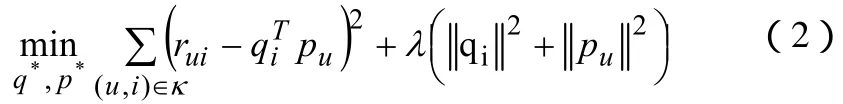
其中λ为惩罚因子。给定惩罚参数的目的是为了防止模型产生过度拟合。

最小化公式（2）有两种方法:梯度下降法[2]和交替最小二乘法。一般情况下，梯度下降法能够在短时间内获得不错的预测精度。交替最小二乘法某些场合能够获得更好的预测精度，但需要花费更长的计算时间。本文实验中采用的是梯度下降法。

梯度下降法的实现方法大致如下:

首先，对每一个给定的训练实例，算法预先给定rui的值（实验发现预先给定的预测值并不影响最终结果）并计算预测值与实际值之差为公式（3）

然后，算法根据预测值与实际值之间的偏差调整iq与pu的参数，调整公式为公式（4）、（5）

其中γ为学习率，λ为惩罚因子。往往更小的学习率能够获得更好的预测精度，但同时需要更多的学习时间。加入惩罚因子的目的是为了防止模型产生过度拟合的情况。

2.2 加入偏差的矩阵分解模型（BMF）

基本矩阵分解模型主要捕捉到的是产品与用户之间的作用关系，而并没有考虑每个用户与每件产品本身之间的差异性。例如，某些用户对产品的评价普遍偏高，而某些用户对产品的评价则普遍偏低。有些产品性价比很高，从而获得更高的评价；而有些产品可能本身质量问题，从而获得较差评价。

因此，很难仅仅通过qi、pu解释所有的评分。我们可以在捕捉产品与用户的相互关系之前消除上面提到的偏差，从而获得基准预测，如公式（6）

其中μ为所有训练集上的均值，bu和bi分别为用户u和产品i在训练集上相对于均值μ的偏差。

那么考虑偏差后的预测评分公式（7）

类似于基本矩阵分解模型，我们可以最小化训练集上的均方误差学习这些参数如公式（8）

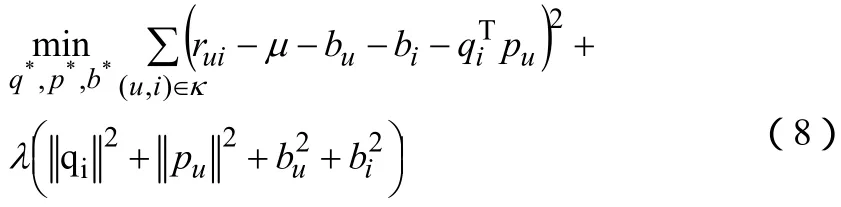
同样地，我们可以使用梯度下降法最小化公式（8）。

2.3 考虑时间效应的矩阵分解模型（TBMF）

在上一节中，产品偏差bi和用户偏差bu并没有考虑时间效应，但在实际生活中，我们会发现用户的喜好和产品的欢迎度均受时间的影响，如图1所示:

描述的是Netflix电影评分系统随着时间的推移，评分均值的变化情况。从该图中可以看出，时间因子确实影响着系统评分。接下来，我们将在改进模型中加入时间因子，捕捉这些时间效应，从而获得更好的预测结果。

考虑时间效应后，我们改写公式（6），用户u在时间tui对产品i的基准评分预测计算公式（9）

在该公式中，bi和bu的值在不同的时间点，所获得的值是不同的。

Koren[3]认为，一件产品的欢迎程度一般不会在很短的时间内发生变化（在某些特殊情况下不适用，例如2003年非典时期食用醋的价格飙升）。因此，我们在捕捉产品的欢迎程度变化情况时，没有必要捕捉每天的变化值。如果捕捉每天的变化值，不仅需要大量的存储空间和计算量，而且会降低执行效率。我们可以选择一个固定周期（bin），周期的长短视具体产品类型而定。例如在Netflix电影评分系统中，用户一般在周末对电影的评分较多，那么我们可以选择周期为星期的倍数。实验证明，按星期的倍数为周期划分的效果比其他的划分方式好。我们假设划分的周期数为K，产品i在第k个周期获得的评价得分均值为，那么我们可以给出bi(t)的计算公式（10）

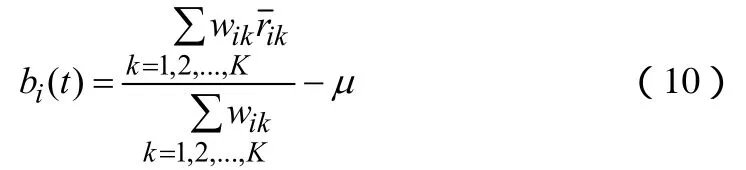
wik的计算方法为公式（11）

为了防止过度拟合，需要修正的值公式（12）

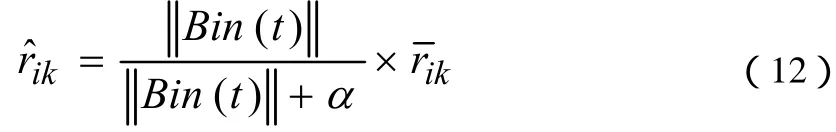
α的值能够通过交叉验证（cross validation）获得。那么最终bi(t)的计算公式为公式（13）

在计算考虑时间因素的ub时，我们不能够简单的套用计算ib的方法。其主要原因是:用户对产品的评分除了相对稳定的喜好外，受当天的情绪波动影响较大，如果简单地将用户对产品的评分划分为一段一段的形式，将丧失用户每天的情绪波动信息。

为了捕捉用户喜好的变化，Koren提出了时间偏差（time deviation）的计算公式（14）

其中为用户u的平均评分时间，表示时间t与之间间隔的天数，β的值能够通过在验证集上交叉验证获得。那么我们可以给出bu的计算公式（15）

公式（15）中并没有考虑用户每天的情绪波动信息，我们可以在公式（15）的基础上加入评分日当天的偏差信息为公式（16）

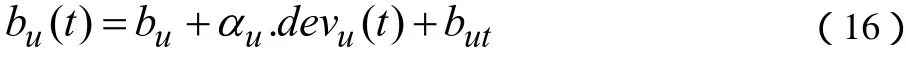
我们可以给出一种简单的计算utb的方法，如公式（17）

为了防止过度拟合，我们需要在公式（17）中加入惩罚因子，如公式（18）

α的值同样可以通过交叉验证的方式求得。

那么综合前面的公式，我们给出计算uib的完整公式（19）

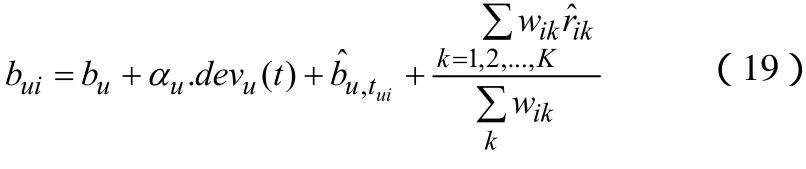
相应的，考虑时间效应后的的预测评分公式为:

类似于基本矩阵分解模型，我们可以最小化训练集上的均方误差学习这些参数:

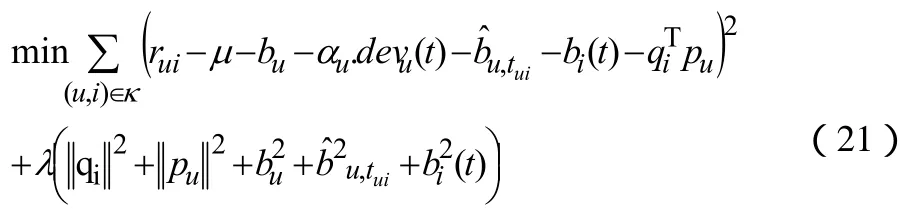
同样，我们可以选择梯度下降法最小化公式（21）。

3 实验结果与分析

3.1 Netflix电影评分数据集

本文中实验所用数据集为Netflix公司于2006年10月份对外发布的电影评分数据集。该数据集包括了从1999年12月31日到2005年12月31日的超过一亿条评分。这些评分来自于480,000多位匿名用户对17,770部电影的评分，每条评分包含了评分日期。在该数据集中，平均每部电影有5,600个评分，平均每个用户评价了208部电影。本文中实验结果的验证均在Netflix公司发布的Probe set上进行，对预测结果的好坏评价采用的是均方根误差（root mean squared error）方法。RMSE的计算公式（22）

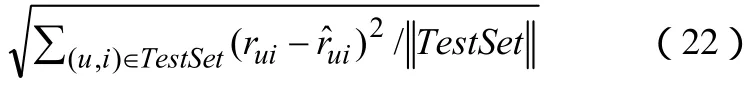
Netflix数据集是在Netflix Prize竞赛中发布的。Netflix Prize竞赛的的目标是提升该公司的推荐系统，其推荐效果须在Netflix公司使用的推荐系统Cinematch的基础上改进10%（使用均方根预测误差衡量）。Cinematch系统作为Netflix公司所使用的推荐系统，在测试集（Probe set）上的RMSE值为0.9514。

3.2 实验结果

本文实验所用测试集与验证集均使用Netflix于2006年发布的电影评分数据集，该数据集不仅数据量庞大，而且经过Netflix公司利用科学方法从真实的电影推荐数据库中提出出来，从而能够很好地模拟现实中的推荐系统。

本文分别实现了未考虑时间效应、加入电影的时间效应、加入用户的时间效应后的基准评分预测结果，使用的公式如下:

不考虑时间效应:bui=μ+bi+bu，

加入电影的时间效应:bui=μ+bi(t)+bu，

加入用户的时间效应:bui=μ+bi(t)+bu+αu.devu(t)+but。

表（1）给出了利用上面3个公式计算出来的预测偏差RMSE的值，如表1所示:

表1 加入时间效应前后的基准评分预测结果

从实验结果给出的数据来看，考虑电影的时间效应后，预测误差确实有所减少。而相对于电影的时间效应，用户的时间效应对预测精度的影响则更大。考虑用户的时间效应后，预测精度得到显著提高。这也说明了用户的偏好变化尤其是每天的情绪波动对电影的评分影响显著。

如图2所示:

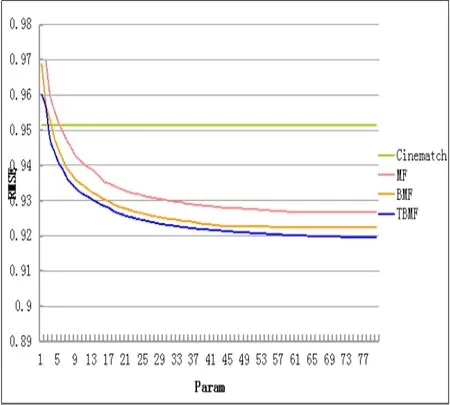
图2 MF、BMF、TBMF模型在netflix数据集上的RMSE变化图

给出的是基本矩阵分解模型、未考虑时间效应的BMF模型和考虑了时间效应的TBMF模型应用梯度下降法给出的RMSE变化情况。图中还给出了Netflix公司在该数据集上的RMSE值。

从图2可以明显看出，加入时间效应后的矩阵分解模型在Netflix电影数据集上获得了更好地预测精度。

4 结论

矩阵分解技术作为潜在因子模型的重要实现方式，在推荐系统中得到了很好的应用。由于基于该技术的矩阵分解模型具有很好的可扩展性，我们在基本矩阵分解模型中加入了具有时间效应的产品偏差和用户偏差，成功地捕捉到了产品的评价偏移、用户的喜好偏移和用户每天的情绪波动对评分的影响。考虑了时间效应后，预测偏差明显减小，预测精度显著提高，从而获得更好的推荐结果。

[1]Y.Koren,R.M.Bell,C.Volinsky.Matrix factorization techniques for recommender systems[J],IEEE Computer 42(8)(2009)30-37.

[2]B.Webb.Netflix update:Try this at home[EB/OL].http://sifter.org/-simon/journal/20061211.html,2006-12-11.

[3]Y.Koren.Collaborative Filtering with Temporal Dynamics[J].ACM Press,2009,pp.447-456.