混合多个SVR模型的金融时间序列预测

陈钟国

0 引言

金融时间序列预测是现代时间序列研究中最具挑战性的课题。金融时间序列是复杂的非线性动态系统，被认为是非平稳的（non-stationary）、确定性混沌的（deterministic chaotic）并且含有大量噪声[1]。非平稳性说明其分布是时变的；确定性混沌的特性则说明它是短期可预测的；而噪声高则意味着无法从金融市场过去的行为中获取完整的信息，以全面揭示历史价格与未来价格间的依赖关系，模型中不能包含的信息就被视为噪声。

以人工智能为基础的预测方法，如人工神经网络（ANN）、支持向量回归（SVR）等，属于非线性的预测模型，符合金融时间序列的特性，逐渐得到人们的重视[2,3,6]。研究[3,5]表明，SVR的预测结果明显优于ANN。本研究将使用SVR建构金融时间序列预测模型。

SVR的精确性和泛化能力，很大程度上依赖于核心函数及超参数。本研究将采用粒子群优化算法（PSO）来确定超参数及核函数的参数。

由于金融时间序列具有非平稳性等特征，其统计特性可能随时间而发生变化。单一的SVR模型不能有效地揭示数据的非平稳性，其预测精度容易出现波动。针对这一问题，本研究提出一种混合多个SVR模型的算法，选取训练数据的不同子集训练出多个SVR模型，预测时通过对多个SVR模型的预测结果加权求和而得到最终预测结果，各个SVR模型的权重根据其预测精度动态调整。通过选择合适的子集，并采用合适的权重更新算法，可以尽量保证在某些模型预测精度出现波动时仍能找到预测精度较高的模型，降低因金融时间序列的非平稳性而使预测精度降低的风险。

实验表明，本文提出的算法，能有效地提高金融时间序列预测的准确性。

1 研究方法

1.1 支持向量机（Support Vector Machine，SVM）

SVM是Vapnik等学者在统计学习理论基础上提出的分类方法，建立在VC维理论和结构风险最小化（SRM）准则基础上。与ANN相比，SVM具有小样本学习、泛化能力强等特点，能有效地避免过度学习、局部极小点及“维数灾难”等问题。

1.2 支持向量回归（Support Vector Regression，SVR）

SVR的主要概念与SVM相同，不同之处在于SVR是以回归模型表示的。设训练样本为{(xi，yi)}（i=1,2,…,n），输入变量xi∈Rm是一个m维向量，输出变量y∈R是一个连续值，n为样本个数。SVR的目标就是构造如下的回归函数，公式（1）

其中Φ(x)可将输入变量非线性映射到高维空间，将原本非线性可解的问题转换成在高维空间线性可解的问题。为确定上式中的系数w、b，可最小化，公式（2）

其中，第一项为经验风险（误差），第二项为结构风险（用来预防发生过度学习问题）；C为修正系数。经验风险通过下式的ε-不敏感函数进行计算，公式（3）

该函数定义了一个管状区域，ε为管状区域宽度，当预测值落在管状区域内时损失为零，预测值落在区域外时，其损失相当于预测值与区域边界的差。

通过引入松弛变量（slack variables）ξ及ξ*，可将上述问题转化成二次规划问题，公式（4）

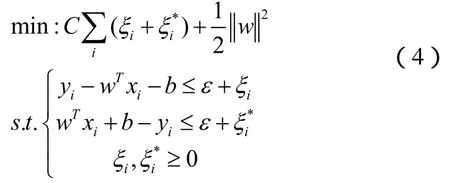
该问题可通过拉格朗日乘子法求解，决策函数（decision function）有如下形式，公式（5）

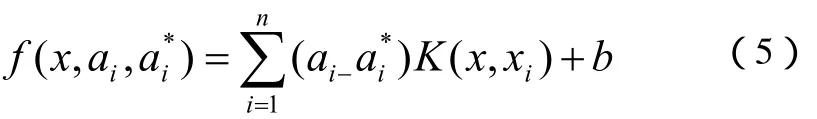
其中ai和ai*为拉格朗日乘子，满足aiai*=0，ai≥0，ai*≥0，i=1,…,n，可通过下列最大化对偶函数（dual function）求得，公式（6）

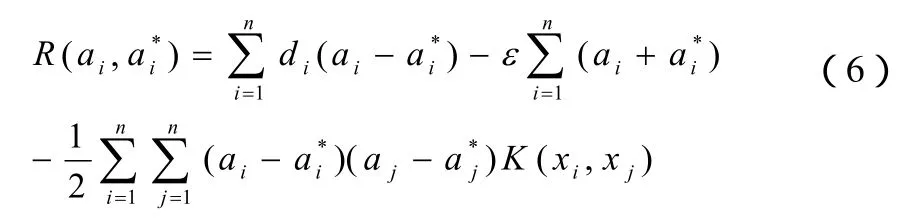
约束条件为:

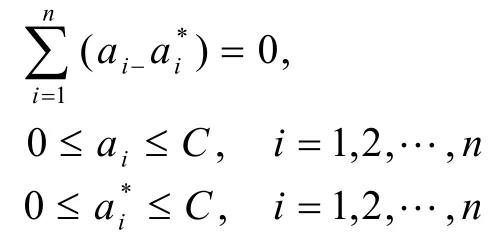
根据二次规划问题的Karush-Kuhn-Tucker(KKK)条件，决策函数中仅有特定数量的系数(ai-ai*)非零。这些系数所对应的数据点被称为支持向量。决策函数只需要这些数据点即可确定。一般而言，ε越大，支持向量的个数越少，解的形式也就越稀疏，但在训练误差越大。

K(xi,xj)为核心函数，K(xi,xj)=Φ(xi)*Φ(xj)。

使用核心函数，可以处理任意维度的特征空间，只需在特征空间进行内积运算，不必显式地将变量映射到高维空间。

任何满足Mercer条件的函数都可以当作核心函数。典型的核心函数有多项式核心函数、径向基函数（Radial basis function，RBF）等:

核心函数的选择至关重要，因为它间接定义了变量所映射到的高维特征空间的结构，从而影响解的复杂程度。RBF函数已被广泛地应用于基于SVR模型的金融时间序列的预测[2-3]。在本研究中也使用RBF核作为核心函数，因为RBF核能够实现非线性映射，一般不会出现太大偏差，且仅需调整参数γ。

1.3 SVR超参数及核心函数参数的选取

SVR的泛化能力（预测精度）很大程度上依赖于SVR超参数和核心函数参数的选择。选定RBF作为核心函数后，需要调整的参数为:修正系数（C）、管状区域宽度（ε），RBF核的参数（γ）。

（1）交叉验证法

参数选择的基本思路是:通过尝试不同的参数组合，比较其预测精度，选出预测精度最高的参数组合。

交叉验证法是衡量模型精度的一种常规方法。例如使用10折交叉验证，就是将训练数据集分成10份，轮流将其中9份做训练1份做测试，10次的结果的均值作为对精度的估计。模型的精度通常用均方根误差（RMSE）进行衡量，RMSE越小，精度越大，公式（7）

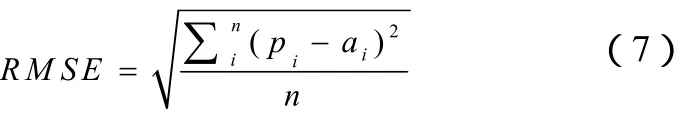
其中，n为测试数据的个数，pi为预测输出，ai为实际输出。

（2）使用PSO算法确定参数

为了确保SVR模型的预测精度以及减少计算量，本研究采用PSO算法确定上述参数，PSO算法具有流程简单、容易实现、无需复杂调整的优点，比传统的网格搜索具有更高性能。

粒子的位置代表一种参数组合(C,ε,γ)，使用该参数组合在训练数据上采用5折交叉验证法得到RMSE，粒子的适应度的计算公式为（8）

实验中，SVR参数选择范围为:C=[2,1000]，ε=[0.001,0.2]，γ=[0.0001,2]；采用的PSO参数为:c1=1.9，c2=1.9，r1=1.2，r2=1.2，ωstart=0.8，ωend=0.2，tmax=50，粒子个数为20。

使用上述参数运行PSO算法，当达到最大迭代次数或所得解不再变化，就终止迭代。

（3）其他方法

由于本研究需要进行大量实验（尤其是在研究SVR输入参数、输出参数的选择的时候），为减少实验时间，还考虑了其他选择参数组合的方法。

当ε处于合理的范围之内时，ε的变动对SVR模型的影响不明显[3]，因此在部分实验中取ε=0.001。

实验中发现，当γ不变时，C的变动对SVR模型的影响不明显。为了进一步节省实验时间，在部分实验中选择C=3σy，其中σy为训练数据集中输出变量的标准差。

1.4 SVR输入向量、输出变量的选择

时间序列包含一系列标量数据，因为一般认为时间序列的下一输出与时间并不直接相关，而与系统状态有关，所以必须选择合适的输入向量，以重构状态空间。重构状态空间的方式包括过嵌入法（over-embedding）、特性向量法（feature vector）。

使用过嵌入法[5]，必须选择合适的维度m、时延d，在时刻i，输入向量为{pi,pi-d,…,pi-(m-1)d}，输出变量为pi+d（pi为时刻i的价格）。对于金融时间序列，目前还没有系统化的方法可以确定合适维度和时延。常规的方法，如互信息法[5]、伪邻点法[5]，由于金融时间序列噪声比较高，效果并不理想。

特性向量方法，指的是考虑当前时间点往前的一个时间窗口，将其中的数据压缩成几个特性值，作为输入向量。如果选择的是合适的特性，输入向量的维度往往小于过嵌入法。

本研究采用的是特征向量法，特征的选择参考了文献[3]的方法。假设选定的输入向量维度为m，时延为d。在每个时间点j，输入向量为{RDP1,d，…，RDPm-1,d，EMA15}，输出变量为RDPd:

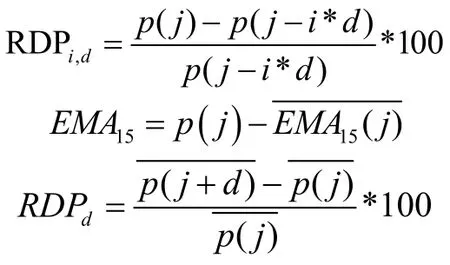
其中p(j)为时间点j的价格。EMA15的计算方法为:当前价格减去15日EMA（指数移动平均）价格。计算RDPd时必须先求得当前以及d天后的3日EMA价格。用EMA平滑化数据，可以提高模型的预测性能[3]。

对于输入向量维度和时延的选择，采用的是穷举法:尝试各种维度和时延的组合，使用单一SVR模型的方法进行预测，计算预测误差。由于这一过程相当耗时，实验中采用了采用1.3节第3小节中的方法确定C、ε，并将γ的选择范围限定为{0.001,0.005,0.01}。

1.5 混合多个SVR模型的预测算法

单一SVR模型的主要问题在于不能有效处理非平稳的金融时间序列。某一SVR模型在各个时间段的预测误差（用NMSE表示），如图1所示:

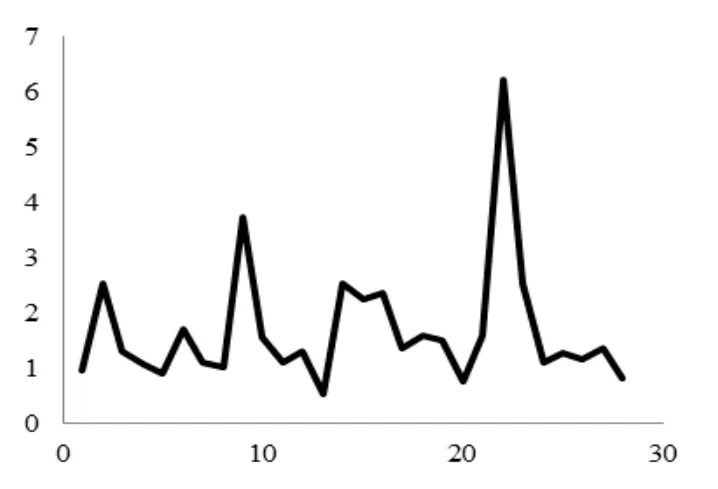
图2 某一SVR模型在各个时间段的预测误差

从图1可以看出，同一SVR模型在不同时间段的预测误差可能出现较大波动，例如在时间段22处预测误差骤增，这种情况通常表示当前时间段的统计特性发生变化，已经和训练数据的统计特性不一致。

为了解决单一SVR模型的问题，我们选取训练数据的不同子集，从中训练出多个SVR模型，分别用这些模型进行预测，并分析了这些模型在各个时间段的预测误差，部分模型的预测误差，如图2所示:

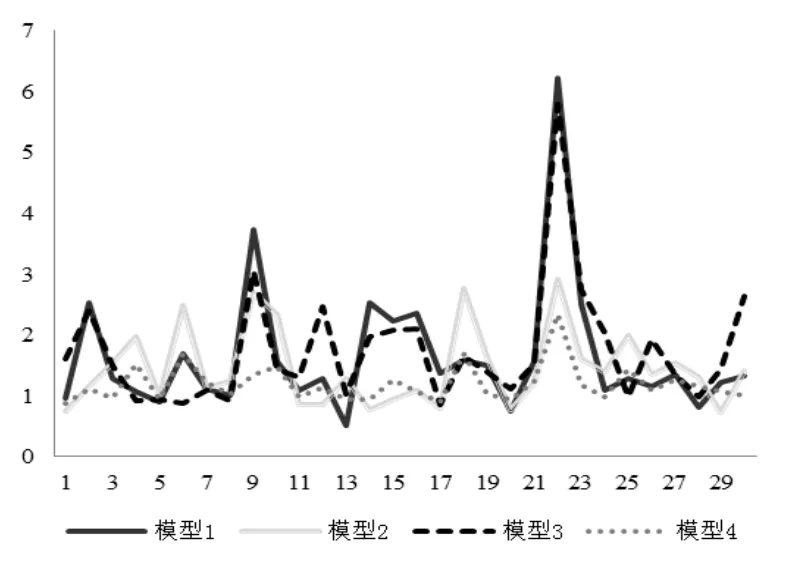
图2 多个SVR模型在各个时间段的预测误差

从图2中可以看出，虽然存在所有模型的预测误差同时骤增的情况（如时间段22处），但通常情况下，在某些模型误差骤增时，其他模型的误差仍然保持平稳。根据这一规律，为了降低某些SVR模型误差骤增所造成的影响，本研究提出一种混合多个SVR模型的算法，通过对多个SVR模型的预测结果进行加权求和而得到预测结果，公式（9）

其中，K为模型的个数，fi(x)为模型i的预测结果，wi为模型i的权重，f(x)为最终的预测结果。由于最终的预测结果综合考虑不同模型的预测结果，在部分模型出现较大偏差时，如果其他模型的预测准确性较高且权重足够大，就能够抵消误差骤增所造成的影响。

各个SVR模型的权重根据其上一轮的预测误差动态调整:

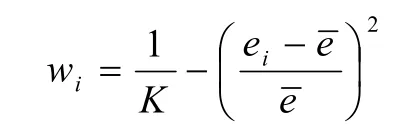
其中，K为模型的个数，ei为模型i在上一轮的预测误差（如:预测值与实际值之差的绝对值），为所有模型在上一轮的预测误差的平均值。容易看出，上一轮预测精度较高的模型权重更高，式中取平方的目的主要是为了进一步增加其权重。由于金融时间序列有短期平稳的特点，多数SVR模型的预测精度在短时间内保持稳定，所以这种更新权重方法能够提高下一轮的预期预测精度。这里只根据上一轮的预测误差调整权值，是为了及时降低误差骤增的模型的权重从而抵消其影响。实验也证实:如果考虑更早之前的预测误差，预测精度并没有得到提高。实验中还发现，如果只选取权重较高的约25%的模型进行预测，预测精度比使用全部模型更好。上述权重还需归一化:

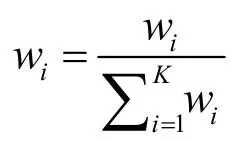
为了尽量确保在某些模型的预测精度出现波动时仍能找到预测精度较高的模型，必须选取合适训练数据子集。本研究采用的方法是:分别将训练数据平均划分为2、3、4、5、6、10个分区，得到共30个分区。

2 实验

2.1 数据集

为验证本文提出的算法，使用表1中所列的指数进行实验，如表1所示:

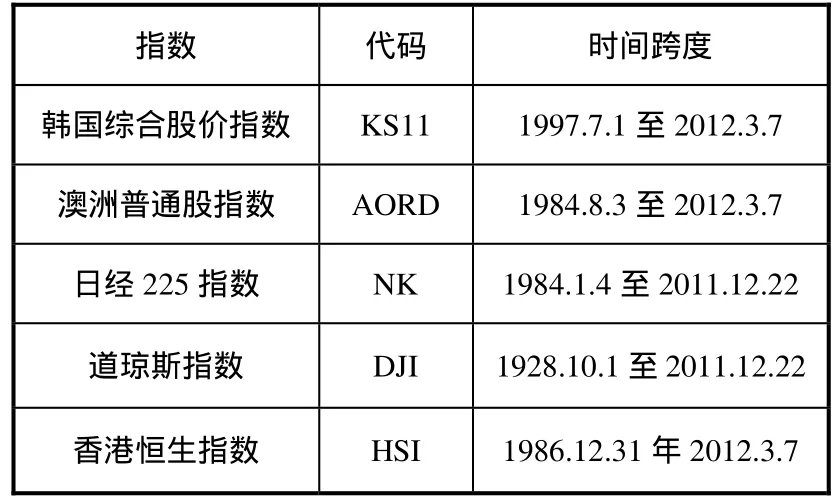
表1 所用指数及其代号

数据从Yahoo Finance网站获得，原始数据包括了每个交易日的开盘价、收盘价、最高价、最低价、交易量等，实验中使用的是收盘价。数据集所跨越的历史时期包含众多重大的经济事件，应该足以验证本文所提出的混合多个SVR模型的算法在非平稳的金融时间序列上的表现。

2.2 数据预处理

首先根据1.4节的方法计算每个时间点的输入向量及输出变量。实验时采用维度m=5，时延d=5。

超出±2倍标准差范围的RDP值被当作异常值，用与之相近的边界值代替。

由于RBF函数对所有特征采用相同处理，从而赋予各个特征相同的权值，数值范围较大的特征比数值范围较小的特征影响更大。为了平衡各个特征的影响，将输入向量各维的数据归一到[-1,1]。

2.3 衡量指标

为了衡量模型的预测能力，采用衡量指标包括:RMSE（root mean square error，均方根误差）、NMSE（normalized mean squared error，归一化均方误差）、WDS（weighted directional symmetry，加权方向对称性），公式（10）

其中，n为测试数据个数，pi为预测输出，ai为实际输出。

RMSE、NMSE都衡量了模型的预测误差，值越小，表示模型的预测精度更高。不同的是，NMSE将测试数据本身的方差考虑在内。

WDS不仅衡量预测误差，还考虑方向准确度。WDS越小，则表示模型越好。这一指标对于市场交易者更有实际意义，因为交易者关心的往往是未来的价格的走势而非具体价格。

需要说明的是，计算WDS时，必须先将输出变量转换成价格。

2.4 实验方法

对上述5个指数的数据进行预处理，将转化后的数据集的前90%作为训练数据，后10%作为测试数据。

实验中分别考察了单一SVR模型和混合多个SVR模型的算法（混合模型）的预测能力。

单一SVR模型使用全部训练数据训练出一个SVR模型，并用该模型在测试数据上进行预测。

混合模型先将选择训练数据的不同子集，再在各个子集上进行训练，得到多个SVR模型，再利用前文描述的算法在测试数据上进行预测。

训练时，使用PSO算法寻找在训练数据上交叉验证误差最小的SVR超参数及核心函数参数。

2.5 实验结果

列出了各个指数上的实验结果，如表2所示:

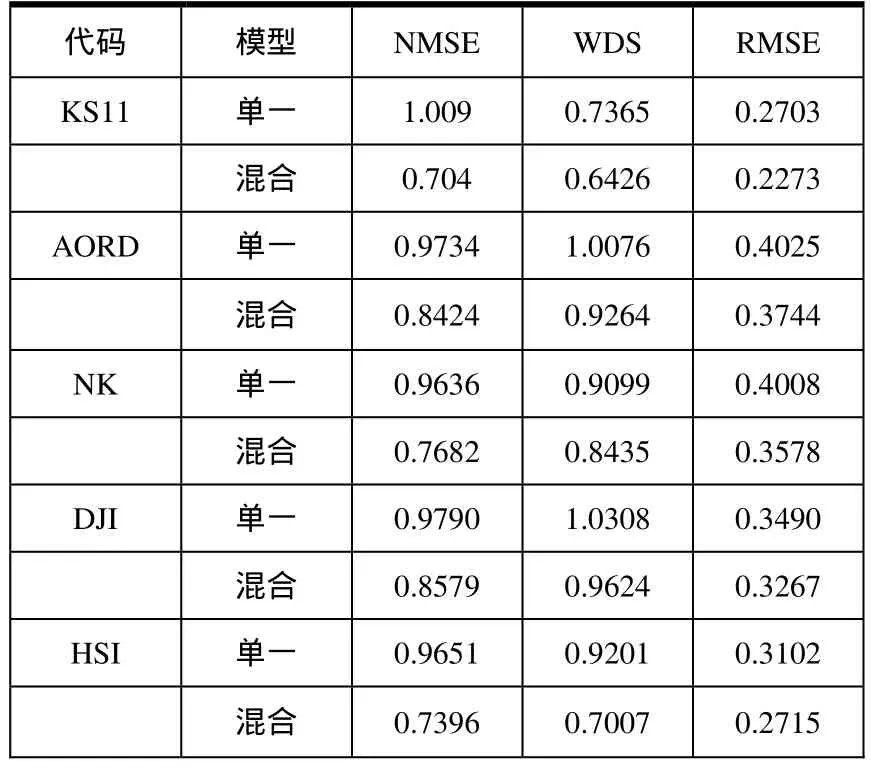
表2 实验结果

同一结果，如图3所示:

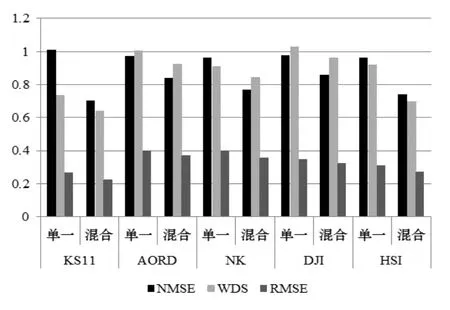
图3 实验结果

实验结果显示，与单一模型相比，混合模型的预测误差（NMSE）降低了10%～30%，而WDS也降低了5%～25%。由此可见，混合模型的预测能力明显优于单一模型。

为了分析模型的预测误差随时间变化的情况，将预测结果根据时间分为30个时间段，计算每个时间段的RMSE。混合模型与模型中用到的各个SVR模型的预测误差（RMSE），其中黑线表示混合模型，如图4所示:

图4 混合模型预测误差与其他模型的对比

在各个时间段，混合模型的预测误差基本上都低于其他模型。由此可见，混合模型确实能够有效处理非平稳的金融时间序列，在市场出现结构性变动时仍能保持较高的预测准确度。从图4中可以看到，在各个时间段，当某些模型的预测误差骤增时，仍有其他模型的预测误差保持稳定，这说明所选择的训练数据子集具有互补性，而权重的调整算法也较合理，能有效抵消非平稳性的影响。

但是，时间段22处的预测误差仍然较大，这可能是因为选择训练数据的子集的算法还有待改进，也有可能因为市场在该时间段的可预测性较低，在后续研究中将继续研究这一问题。

3 结语

本文提出一种混合多个SVR模型的金融时间序列预测算法。在全球5大股指上的实验表明，与单一SVR模型相比，该算法预测金融时间序列的能力有显著提升。这种改进主要是由于算法考虑了时间金融序列的非平稳性，采用不同的数据训练出多个SVR模型，通过合理调整各个模型的权重来抵消某些模型出现波动而造成的影响，从而提高整体的预测精度。

后续研究中将进一步优化算法，继续分析SVR输入向量的维度、时延对算法预测能力的影响，并将该算法应用于其他非平稳时间序列，考察算法的通用性。

[1]Yaser S A M,Atiya A F.Introduction to financial forecasting[J].Applied Intelligence,1996.6:205 13.

[2]Lu C J,Lee T S.Financial time series forecasting using independent component analysis and support vector regression[J].Decision Support Systems,2009.47(2):115-125.

[3]Tay F E H,Cao L J.Application of support vector machines in financial time series forecasting[J].Omega,2001.9(4):309-317.

[4]Kantz H,Schreiber T.Nonlinear time series analysis[M].2nd ed,Lundon:Cambridge University Press,2004.

[5]Samsudin R,Shabri A,Saad P.A comparison of time series forecasting using support vector machine and artificial neural network model[J].Journal of Applied Sciences,2011.10:950-958

[6]Hadavandi E,Shavandi H,Ghanbari A.Integration of genetic fuzzy systems and artificial neural networks for stock price forecasting[J].Knowledge-Based-Systems,2010.23(8):800-808.