基于遗传算法的城市轨道交通运行图自动调整的仿真研究

杨 柯，孔繁虹

（同济大学 电气工程系，上海 200331）

列车自动监控系统（ATS），它主要实现对列车运行的监督和控制，辅助行车调度人员对全线列车进行管理，对提高运输效率和保障行车安全起到重要作用。其中列车运行图是该系统中工作计划与调整基础，在基于通信的列车控制（CBTC）中，列车是基于运行图行驶的，由于列车行驶中存在许多不确定性，经常出现列车实际运行图偏离计划运行图的现象，这时就要进行列车自动调整（ATR），使列车恢复正点运行。

本文对一些论文中已有的遗传算法调整模型做了修改，比如考虑到列车早点的情况，加入了早晚点列车数目的判断标准以及修改了约束条件等，以保证更接近CBTC的真实情况。仿真是在matlab7.5遗传算法工具箱中进行，该工具箱拥有图形界面（GU I），封装了遗传算法的很多函数，将编写好的M文件放入并设置好参数即可运行，比以前单纯编程求解方便许多。仿真结果也证实该算法即方便又可靠。

1 运行图

1.1 运行图介绍

列车运行图表示列车在铁路各区间运行时刻及通过时刻的线条图，记录了列车在每一站到达和出发时刻，以及站之间通过时间和车站之间距离等信息。在运行图上，横坐标表示时间，竖直线为时间等分，称为时分线；纵坐标表示车站距离，横直线为站名线，表示各个车站到发线中心的位置。斜线表示列车运行线，运行线与水平线的交点表示列车到、发和停站时间。常用的运行图有十分格运行图和二分格运行图。

（1）十分格运行图：横坐标以10 min代表一格，0.5 h用虚线表示，h用实线表示。

（2）二分格运行图 ：横坐标以2 min代表一格，对10 min的倍数用粗线表示（如30 min和60 min线），其他用细线表示。

1.2 运行图绘制

运行图表示的是列车的时刻表信息，所以需要数据库来存放车站信息及时刻表信息等，这里采用SQL2005存放数据，绘图则采用mFC的绘图函数，大致步骤为：

从数据库中读取列车的相关数据,如车站信息和上下行时刻表信息等。并分别将时间和车站距离对应的秒数转化为像素数据保存在数组中。如12:00:00是43 200，对应X轴；车站距离对应Y轴。然后用mFC里的for循环和绘图函数move to和line to即可绘制出运行图。

如图1所示，用Visual C++2005的对话框绘制出二分格运行图，横坐标一格代表2 min，纵坐标表示各站之间相对距离；左边蓝色的线表示上行的3辆列车，右边红色的线表示下行的3辆列车，拖动水平滚动条可显示从5:50:00首班车一直到末班车所有的列车运行线（本图只显示到7:10）。

图1 二分格运行图

2 遗传算法

遗传算法的基本原理如下：

（1）编码：把一个问题的可行解从其解空间转换到遗传算法所能处理的搜索空间的转换方法称为编码。

（2）选择：是群体中选择生命力强的个体产生新群体的过程。使用选择算子，适应度高的个体被遗传到下一代群体中的概率较大。

（3）交叉：是按较大的概率从群体中选择2个个体，交换2个个体的某个或某部位。交叉运算产生子代，子代继承了父代的基本特征。

（4）变异：以较小的概率对个体编码串上的某个或某些位值进行改变，生成新个体。

（5）适应度函数：根据目标函数确定的用于区分群体中个体好坏的标准，适应度函数非负的，任何情况下越大越好。而目标函数可能有正负，或求最大值和最小值，因此需要在目标函数与适应度函数之间进行变换

（6）约束条件：一般采用惩罚函数法，对不满足约束条件的个体计算其适应度时，处一个惩罚函数，降低该个体适应度，使该个体被遗传到下一代的概率减小。

3 列车自动调整模型

3.1 模型的建立

列车自动调整的目的是使列车的实际到站和发车时间与计划到站发车时间绝对值最小。由于列车运行是一个连续的系统，某辆车的晚点可能会引起后面几辆车的晚点，为了使列车受到影响的范围最小化，实施运行调整的范围也尽量小。

3.2 编码

编码就是解得遗传表示。为方便求解可以采用直接整数编码的方式，用时间对应的秒数进行编码。如12:00:00秒数是43 200，编码表示就是43 200。

具体编码可采取矩阵的形式:

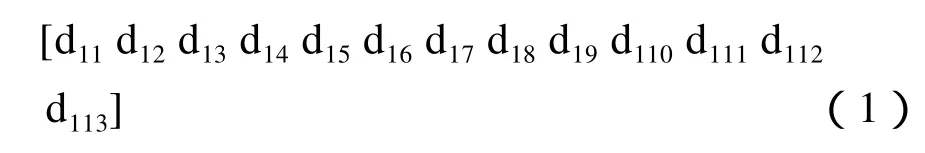
公式（1）表示第1辆车在各站的到站时间，同理第2辆车为d21～d213,发车时间为f21～f213。

3.3 目标函数确定

列车调整有2个目标：

（1）列车到达早晚点时间绝对值与列车发车早晚点时间绝对值总和最小。

其中：n1为上行列车数，n2为下行列车数，m是车站数目。分别为列车实际到站、离站时间di;k, fi;k分别为列车计划到站、离站时间。

（2）列车到达早晚点数目和出发总晚点数目

上式表示列车到站和发车误差小于10 s时不算晚点，大于10 s时该列车晚点，早晚点数记一次。

这样可得出列车调整目标函数为Z=Z1+Z2：

其中w1、w2为权重值，根据实际情况确定。

3.4 约束条件的处理

约束1：发车条件约束，实际发车时间不能早于计划发车时间。

约束2：最小停站时间约束，实际停站时间不能小于最小停站时间。

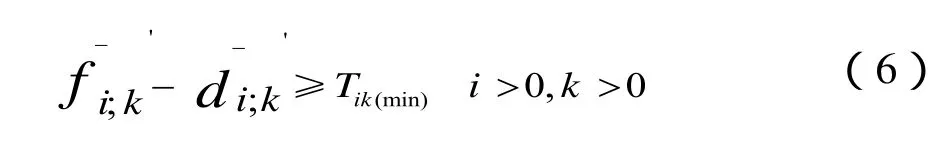
约束3：最小区间运行时间约束，2站之间运行时间不能小于最小运行时间，其数值与线路限速有关。

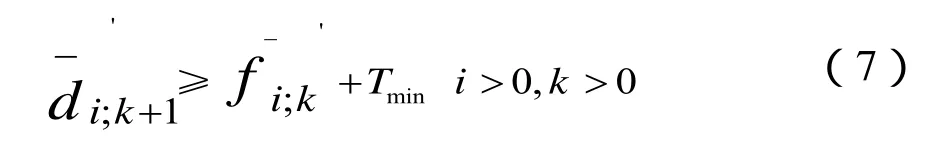
约束4：列车追踪时间约束，相连2辆列车运行间隔不能小于规定的运行间隔，以保证行车安全。

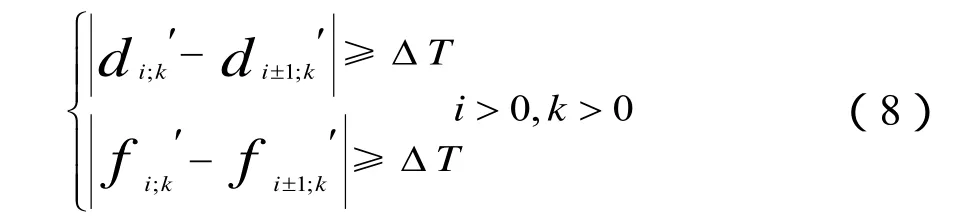
3.5 遗传算法参数确定

本例采用的是matlab7.5中自带的遗传算法与直接搜索工具箱，它有一个图形用户界面GUI，可以直接输入各参数。遗传算法的主要参数有种群参数、选择参数、再生参数、变异参数、交叉参数、迁移参数和停止条件参数等。

种群参数：本例由于变量较多，所以种群规模应该尽量大，一般为300～500之间。

选择参数：通过保留最优个体的选择方式，一般采用轮盘赌选择算法，个体被选择的概率用公式表示

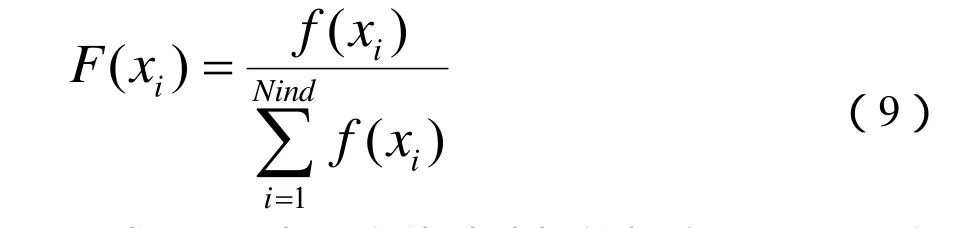
公式（9）表示个体被选择的概率，f(xi)是个体xi的适应度值，Nind是个体数量。该选择方式考虑了适应度对选择的影响，保留了最优个体，防止早熟现象出现。

再生参数：指定将生存到下一代个体数，一般取小于等于种群尺度的正整数，缺省值为2。

变异参数：通过小的随机数改变种群的个体而创建变异的子辈。这里采用均匀变异，变异概率取0.01。

交叉参数：交叉是组合2个个体或双亲，为下一代形成新的子个体。本文采用随机配对，2点交叉的方式，即在编码中随机设置2个交点，再进行部分基因交换。

迁移参数：个体在子种群间移动，用一个子种群最好的个体代替另一种群中最差的个体。一般采用默认值。

停站条件：决定什么引起算法的终止。本文设置最大执行代数为600，停滞代数、停滞时间、适应度限和执行时间都设置为Inf，即无限制。

4 仿真结果及分析

以上海地铁二号线的时刻表为例，一共有13个车站，现用3辆车，分上下行共6个车次进行仿真。

各已知条件如下：

（1）车站总数M=13，站名可看图1的运行图；

（2）列车总数N=3×2=6；

（3）列车在各区间的计划运行时分为（时间单位：s，以下类同）：

[70 90 150 150 140 150 150 90 150 150 90 210]；

（4）列车在各站计划停站时间为：

[180 30 30 30 40 30 30 30 30 30 30 30 30 120]；

（5）该区段列车追踪间隔时间为180 s；

（6）列车区间最小运行时分为：

[65 85 137 137 124 137 137 86 135 136 85 193]；

（7）列车最小停站时间为：

[170 25 25 25 35 25 25 25 25 25 25 25 110]。

该仿真过程是一个连续的调整过程，即先确定晚点列车车次、晚点车站和晚点时间，然后由遗传算法预测该车在剩余几个站的到站和发车时间，以保证总晚点时间最小，如果到折返站晚点仍然存在，则继续调整。直到列车恢复正点运行为止。

例如列车1在上行第3站晚点200 s，则遗传算法编码时前2站的实际时刻表编码仍与计划时刻表相同，从第3站发车开始以后几站的到发时间都设成变量求解，直到折返站，若仍然晚点，则对下行时刻继续求解，直到正点运行。比如求得第4站晚点95 s，到13站时仍晚点20 s，则对下行继续循环，若下行到第10站晚点时间为0，则调整结束。

在matlab中用gatool命令打开遗传算法工具箱，将编写好的目标函数M文件train在Fitness function位置设置为@train,同理将约束条件函数转换成矩阵A•x≤b形式,A处填写矩阵A，b写矩阵b,变量个数根据待求解的列车和车站个数计算，本文设置为45；其他参数按照章节3的设定。

具体仿真结果如表1和图2所示，表1为计划时刻表，表2为根据图2结果显示的秒数（只显示了部分变量）换算成调整的实际时间。

图2 遗传算法运行结果

对比两表可以看出，在上行第3站晚点200 s以后经过连续调整，到下行第12站到达时已恢复正点，此后一直按计划时刻运行。从结果可以看出，该算法仿真的结果良好，列车在遵从约束条件情况下缓慢的将列车调整至正点运行，并保证了列车的总晚点时间最小。

表1 列车在上下行、在各站的计划时刻表

表2 列车在上下行、在各站的实际时刻表

5 结束语

本文研究从不同角度修改列车调整模型已保证其更接近真实情况并验证其正确性；并展示了一个更方便的遗传算法求解过程，使求解效率提高。

在实际列车运行中经调整后的数据由ATS中的ATR模块发送给列车自动运行系统（ATO），ATO根据此数据控制列车区间行驶及停站时间，并将实际运行的数据反馈给ATS运行图绘制模块，绘制出实际运行图。可实现列车实际运行图从偏离计划运行图到慢慢恢复到计划运行图的过程，从而实现了列车运行图的自动调整。

[1] 雷英杰，张善文，李续武，周创明.MATLAB遗传算法工具箱及应用[M].西安：电子科技大学出版社，2005：1-258.

[2] 刘洪宽.城市轨道交通ATS关键技术及仿真平台研究[D].成都：西南交通大学，2008：33-53.

[3]马海民，赵庶旭，党建武.基于多目标遗传算法的客运专线列车运行调整[C].全国博士生学术论坛电气工程论文集，2008：1998-2004.

[4] 高强周.城市轨道交通列车运行图设计实现与评价[D].北京：北京交通大学，2008：19-54.

[5] 王慧妮.客运专线列车运行调整模型及算法研究[D].成都：西南交通大学，2006：26-47.

[6] Li Mao jun.COOPERATIVE EVOLUTION GENETIC ALGORITHM ON BIDDING OF POWER MARKET [A].IMACS Multiconference on"Computational Engineering in SystemsApplications"(CESA), 2006.