基于颜色规格化和轮廓多边形的交通标志检测
李 贺, 郝晓莉,齐 飞
(北京交通大学 电子信息工程学院, 北京 100044 )
交通标志在规范交通行为、确保安全驾驶等方面具有重要的意义。交通标志检测是交通标志识别的前提,是智能交通系统的重要组成部分。
国内大多数的交通标志检测文献是针对某种特定形状的交通标志设计检测算法。文献[1~2]基于最小二乘法和圆形度特征检测圆形交通标志;文献[3]基于辐射对称性和Hough变换的方法检测三角形交通标志。国外一些文献提出了可以检测多种形状交通标志的算法。文献[4]结合颜色和形状信息检测感兴趣区域,用相干匹配法确定交通标志的位置,能够检测圆形、三角形、矩形、五边形等美国交通标志。文献[5]在HSI颜色空间构造色调和饱和度分量查找表,实现颜色分割,采用遗传算法进行交通标志检测,能够检测圆形、三角形等西班牙交通标志。
本文采用颜色规格化[6~7]技术,将颜色信息复杂的交通场景图像映射为只含8种标准颜色的图像。选取红、黄、蓝为感兴趣颜色将图像二值化。提取二值图像各连通区域最外层轮廓,对每一轮廓逐一判断。通过轮廓周长、面积、圆形度及本文提出的基于重心的干扰区域判定规则排除干扰区域。对候选区域最外层轮廓进行多边形拟合,通过判断拟合多边形的凸性来判定交通标志候选区域。最后,选取面积最大的候选区域(面积最大说明目标最近)为交通标志区域。本文算法可以检测我国任意形状的交通标志并对交通标志倾斜及旋转的情况具有较好的鲁棒性。
1 交通标志颜色形状信息统计
为了引起行人和车辆驾驶人员注意,交通标志具有鲜明的颜色和形状特征。根据国标GB 5768.1-2009[8],我国指示、禁令和警告标志共131种(警告标志47种、禁令标志48种、指示标志36种),主要包含5种颜色:红、黄、蓝、黑、白。5种形状:圆形、矩形、正三角形、倒三角形、正八边形。其中,矩形包括正方形和长方形,长方形的长宽比范围约为1.3~1.4。警告标志颜色以黄黑为主,形状包括正三角形、矩形和一个叉形标志;禁令标志颜色以红白黑为主,形状包括圆形、矩形、倒三角形和正八边形;指示标志颜色以蓝白为主,形状包括圆形和矩形。131种交通标志中具有规则形状的有130种,并且都为凸多边形。
2 图像预处理
2.1 颜色规格化
颜色规格化将R、G、B3分量分别与给定阈值作比较,把交通场景图像复杂的颜色空间映射到只含8种标准颜色的简单颜色空间,该颜色空间涵盖了我国交通标志所有的颜色种类。设R、G、B3通道的规格化阈值分别是Tr、Tg、Tb,图像中第i个像素点为(Ri, Gi, Bi)。对R通道,根据式(1)进行规格化:

G、B通道规格化方法与R通道相同。规格化产生的标准颜色为红、黄、蓝、绿、青、品红、黑、白,将品红色简并为红色,青色简并为蓝色。具体规格化流程见文献[7]。8种标准颜色分别位于RGB立方体的8个顶点,具有最大的颜色距离,各颜色之间的RGB向量具有正交性。
2.2 图像二值化及形态学处理
选取感兴趣颜色,将规格化后的图像二值化。感兴趣的颜色对应的像素点二值化为255,否则二值化为0。图像二值化以保持交通标志候选区域完整性为前提,最大限度的排除干扰区域。指示标志以蓝色为主,选蓝色为感兴趣颜色。禁令标志边框为红色(8种除外),选红色为感兴趣颜色。警告标志主要以黑色边框为主,而实景图像中黑色干扰较多,如建筑物、车辆、树木的阴影及车窗玻璃、交通灯外壳等。警告标志黑色边框较窄,而黄色内核明显,选黄色为感兴趣颜色。

图1 交通实景图像黑色干扰
图1中,(a)为交通实景图像。(b)为以红、蓝、黑为感兴趣颜色的二值图像。(c)为以红、蓝、黄为感兴趣颜色的二值图像。可见(b)中由于选取黑色为感兴趣颜色,带来了较多干扰。
形态学开运算可以断开交通标志区域与干扰区域的粘连,使各个连通区域保持独立。提取各个连通区域,对各连通区域分别做多次闭运算,这一点非常重要,这样可以确保候选区域闭合,使提取的连通区域轮廓为最外层轮廓。如果对整幅图像做多次闭运算,就会导致相邻区域的粘连。
3 基于形状特征的干扰区域判定规则
颜色规格化和二值化只能排除明显的干扰区域,与交通标志相似(如颜色相近)的干扰区域需要根据交通标志特有的形状特征进一步排除。
3.1 圆形度
实验所用图像大小为500像素×375像素。图像形态学处理后,依据规则1判定干扰区域。
规则1:设连通区域最外轮廓的周长为Perim eter,面积为A rea,如果Perim eter<100像素 或A rea<400像素,则该区域为干扰区域。
丢弃干扰区域后,复制候选区域轮廓到一幅新的二值图像中,并把轮廓内部填充为白色。对该区域进行4次膨胀操作,对膨胀后的区域再次提取最外层轮廓,计算轮廓的圆形度。
圆形度表示图形与圆形的接近程度,可以有效地排除不规则的干扰区域。交通标志轮廓的圆形度理论值见表1。

表1 交通标志图像圆形度理论值
考虑到交通标志的倾斜,以及多次膨胀带来的误差,设定圆形度的阈值为:[0.5, 1.0],不在此范围内的区域判定为干扰区域。
3.2 基于重心的干扰区域判定规则
重心是物体各部分所受重力的合力的作用点,对于形状规则且密度均匀的物体,其重心与形心重合。我国交通标志基本都是规则图形,在二值图像中,交通标志候选区域被填充为白色,可视为密度均匀的物体。重心与候选区域轮廓的相对位置能够很好地描述交通标志的形状特征。对于不规则的区域,重心与轮廓的相对位置有3种情况:重心在轮廓外部、重心在轮廓上、重心在轮廓内部但不符合交通标志的形状特征。针对以上情况定义规则2和规则3,如下:
规则2:重心在区域最外层轮廓的外部或在区域最外层轮廓上,则该区域为干扰区域。
规则3:重心到区域最外轮廓的最大距离为dmax,最小距离为dm in,最大与最小距离的比值为r。设定r的阈值T,如果r大于T,则该区域为干扰区域。
我国交通标志图像,r的理论值见表2。依据表2及实际检测情况,取T=2.3。

表2 交通标志r的理论值
3.3 多边形拟合
我国交通标志的形状基本都是凸多边形,这是交通标志区别于干扰区域的重要形状特征。本文采用道格拉斯-普克(Douglas-Peucker)算法[9],对交通标志候选区域最外层轮廓进行多边形拟合,通过判断拟合多边形的凸凹性来决定候选区域的取舍。
3.3.1 道格拉斯-普克多边形拟合算法
道格拉斯-普克多边形拟合算法的主要思想是以直代曲:根据指定精度,用有限条直线逼近一条曲线。
对于非闭合曲线,将曲线首、尾相连,形成一条直线L。如果曲线上其余各点到直线L的最大距离小于给定的拟合精度,则将曲线上介于直线L两端的所有点舍去,直线L便是该曲线的拟合直线。如果最大距离大于给定的拟合精度,则保留到该直线距离最大的点,以此点为界,把曲线分成两部分,并对这两部分重复上述操作,直到曲线段上的所有点到对应直线的距离小于给定的拟合精度。
对于闭合曲线,首先找到曲线上距离最远的两点,连接这两点把闭合曲线分成两部分,对每一部分的拟合方法参照非闭合曲线。
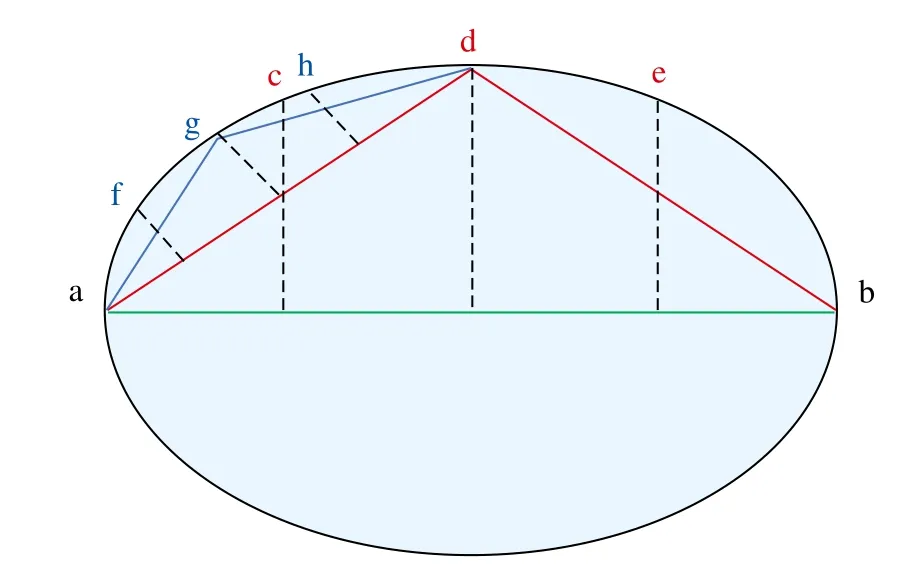
图2 道格拉斯-普克法多边形拟合示意图
如图2所示,对图中的椭圆进行多边形拟合。首先找到椭圆上距离最远点a、b,连接ab把椭圆分为两部分。对于上半部分,求出各点(如图中c、d、e)到直线ab的距离,点d到直线ab的距离最大且大于拟合精度,以点d为界把上半椭圆分为两部分。连接ad、bd。对ad、bd之间的曲线依照上述方法分别处理,直到点到相应直线的最大距离都小于拟合精度,算法结束。
3.3.2 凸多边形判定准则
把一个平面多边形任意一边向两方无限延长成为一条直线,如果多边形的其他各边均在此直线的同一侧,该多边形就叫做凸多边形。
由线性规划的知识,目标函数相同侧的点带入到目标函数中,函数值的符号是一致的。设多边形有N个顶点,其中两个相邻顶点为P(x1,y1)、Q(x2,y2),根据直线的两点式方程,PQ所在的直线方程为,整理可得:

令 t=x(y2- y1)+y(x1- x2)- x1y2+x2y1,把其余N-2个点代入,当且仅当t的值全为正或负时,线段PQ为凸多边形的一条边。遍历多边形的所有边,当且仅当多边形的边都为凸多边形的边,则多边形为凸多边形。
4 实验结果及分析
本文实验以VC++6.0为开发环境,并基于Opencv1.0编程实现。该实验在W indow s XP系统的PC机上完成,处理器为E6700,主频3.20 GHz,内存2 GB,平均检测时间为150 ms。

图3 交通标志检测演示图
图3中,(a)为原始图像,(b)为颜色规格化后的二值图像。提取(b)中交通标志候选区域的最外层轮廓,把轮廓内部填充为白色,并分别做4次膨胀运算后得到(c)、(d)、(e)3幅二值图像。(f)中红色框内区域表示(d)中区域因不满足规则3被判定为干扰区域;黄色框区域为(c)、(e)两区域最外层轮廓的拟合多边形。(e)中区域拟合多边形不是凸多边形,被判定为干扰区域。最终检测结果为(f)中蓝色框标定的部分。
图4中,红色框内的区域,在二值图像中为交通标志干扰区域,因为不满足规则3被排除,红色的点为交通标志候选区域的重心,蓝色框为最终检测结果。可见本文算法可以检测我国任意形状的交通标志。

图4 各种形状交通标志的检测

图5 倾斜及平面内旋转交通标志的检测
图 5 中,(a)、(b)、(c)为倾斜的交通标志,(d)、(e)、(f)、(g)分别为交通标志旋转 30°、90°、120°、210°的情况。重心及交通标志的凸性具有倾斜和旋转不变性,所以本文算法对交通标志倾斜及平面内旋转的情况具有较好的鲁棒性。

图6 不含交通标志图像的检测
图6表明,对于没有交通标志的图像,本文算法没有带来误检。
5 结束语
本文讨论了对颜色规格化后的图像进行二值化操作时,感兴趣颜色的选取问题,得出了以红、蓝、黄为感兴趣颜色引入干扰较少的结论。本文提出了两种基于重心的干扰区域判定规则和一种基于道格拉斯-普克(Douglas-Peucke)多边形拟合算法的交通标志检测方法。基于重心的干扰区域判定规则能够快速有效地排除干扰区域;基于多边形拟合的交通标志检测方法能够检测我国各种形状的交通标志。实验证明,本文算法简单有效,并且对交通标志倾斜及旋转的情况具有较好的鲁棒性。
本文算法的不足之处在于颜色规格化阈值为经验值,鲁棒性较差;算法基于连通区域最外层轮廓进行设计,对轮廓的完整性和独立性要求较高。这两点是后续研究待改进的地方。
[1] 张 静,何明一,戴玉超,屈晓刚.多特征融合的圆形交通标志检测[J].模式识别与人工智能,2011,24(2):226-232.
[2] 简 楹.基于颜色和边缘信息的交通标志检测[J].山西电子技术,2011(3):6-7.
[3] 何江萍,马 彦.基于形状信息的三角形交通标志检测方法[J].计算机工程,2010,36(19):198-199,202.
[4] Jesm in F. Khan, Sharif M. A. Bhuiyan, Reza R. Adham i. Image Segmentation and Shape Analysis for Road-Sign Detection[J]. IEEE TRANSACTION ON INTELLIGENTTRANSPORTATION SYSTEMS,2011,12(1):83-96.
[5] A. de la Escalera, J. Ma Armingol, M. Mata.Traffi c sign recognition and analysis for intelligent vehicles[J]. Image and Vision Computing, 2003,21(3):247-258.
[6] 朱双东,蒋甜甜,刘兰兰.基于颜色规格化的交通标志识别[J].计算机应用与软件,2008,25(1):202-222.
[7] 刘 鑫,扬立敬,朱双东.快速交通标志检测预处理方法[J].计算机工程与应用,2010,46(29):229-231,244.
[8] GB 5768.1—2009. 道路交通标志和标线[S].中国标准出版社,2009,7.
[9] Douglas D H, Peucker T K. A lgorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. The Canadian Cartographer,1973,10(2):112-122.

