中心多元t分布的一致渐近正态性

严琴，唐贺，李开灿

(湖北师范学院 数学与统计学院，湖北 黄石 435002)

在数理统计中许多估计和检验统计量，或服从x2分布，或服从t分布，或服从F分布，人们总是希望证明这些统计量的分布具有渐近正态性，而t分布作为一种重要的概率分布类型，广泛的应用于不确定评价和检验分析等，是概率统计进入实际应用的重要标志，对它的一致渐近态性的讨论是很有意义的.

在文献[1]中，借助于瓦利斯公式给出了t分布的极限分布为标准正态分布，而在文[2]中，引入了新的方法——Kullback-Leibler距离，证明了一元t分布的一致渐近正态性. Kullback-Leibler距离在数理统计和信息论等学科中具有广泛的应用，信息的Kullback-Leibler距离，能够很好地表示两个分布函数所包含信息的差异程度，距离越大，差异程度越大.

本文将一元t分布的渐近正态性的结果推广到多元t分布的情形，而在文[3]中，已经讨论了多元t分布与多元正态分布之间的关系，本文利用两个密度函数之间的 Kullback-Leibler距离，获得了中心多元 t分布的一致近正态性的条件.

1 多元t分布一致渐近正态性的描述

定义1 若随机向量 X =(X1, X2,L ,Xp)¢具有如下的密度函数:

则称X服从自由度为n的中心p元t分布，记作 X ～ Tp(n). 其中n，p是任意的正整数，G(×)表示Gamma函数.

定理1 设 X ～ TP(n)，A是p´p阶常数矩阵，u =(u1,L,uP)¢∈ RP是常数向量. 令 Y = A X +u，则Y是服从自由度为n的p元t分布，记为Y ～Tp(n; u ; S)，其中 S =AA¢为非负定阵.

证明：由 Y = AX +u，可得 X = A-1(Y -u)，故g多元t分布的定义可知Y ～Tp(n; u ; S).

定义 2 若在n维欧氏空间(Rn, Bn)中，随机变量 X , Y分别具有密度函数 f ( x) ,g( x)，分布函数F( x), G( x)，记 F ( E ) = òEd F ( x) , G ( E ) = òEd G ( x),E ∈ Bn，则 f ( x) ,g( x)之间的Kullback-Leibler距离和全变差距离分别为

定义3 若 X ～ Tp(n; u;S), Y ～ Np(u,S)，若当n®¥时，D( X, Y)®0，则称多元t分布Tp(n; u ; S)一致渐近正态分布Np(u , S).

2 基本引理

引理1

注：此引理的证明见文献[4].

引理2 若 X =(X1, X2,L ,Xp)¢～ Tp(n)，则 E ( X ) = (0,0,L ,0),Cov( X, X ) =是p阶单位阵.

证明：根据期望的定义可知

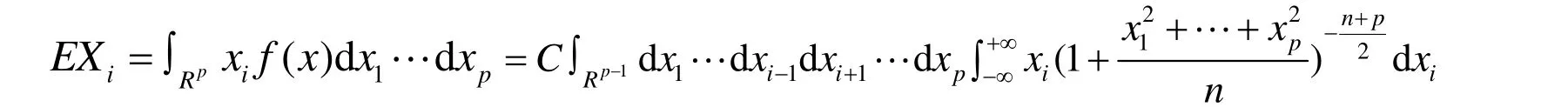
这里òRp表示p维欧氏空间上的积分.

事实上，由于被积函数是奇函数且积分区间是对称的，故 E Xi= 0 i=1,L ,p，所以有E( X ) = (0,0,L ,0 ).下面计算X的协方差阵.当i¹j时，

根据引理1可得到

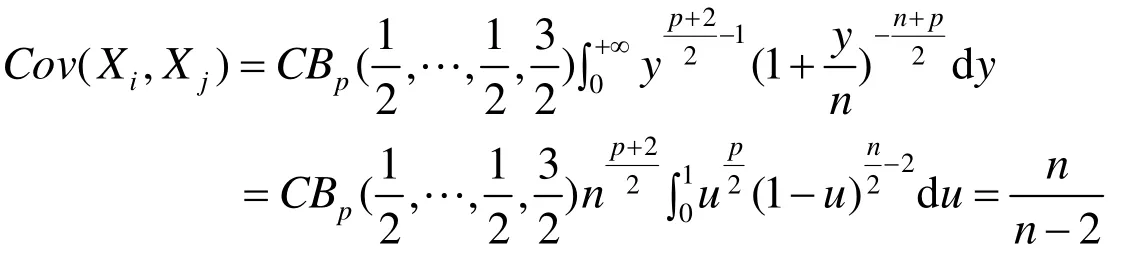
根据随机向量的数字特征的运算性质，很容易得到下面的推论

推论1 若Y ～Tm(n; u ; S)，则E( Y ) = u,

证明：令 Y = AX + u = ( A1, A2,L ,Ap)¢X +u ，其中 A A¢ = S, Ai∈ R1´p, X ～ Tp(n)，则 Yi= AiX +ui，故

则E( Y ) = (u1,L ,up)¢ = u , C ov( Y ) =

兴趣是数学创造的重要动力之一，兴趣是力求探索，获得数学创造的带有情绪色彩的意向活动。学生对数学的迷恋往往是从兴趣开始的，由兴趣产生动机，由动机到探索，由探索到成功，在成功的快感中产生新的兴趣和动机，推动学习的不断成功。

注：此引理的证明可见文献[6-7].

3 结论

定理2 设 X ～ Tp(n)，则有

证明：由于 òRpf( x)dx1Ldxp=1，则

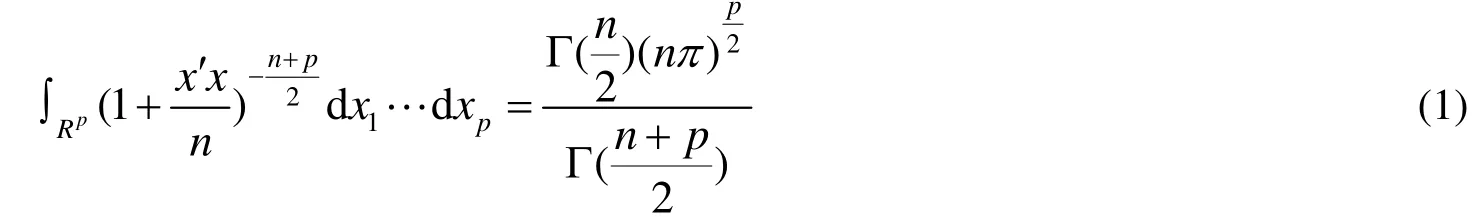
式(1)两端同时关于n求导数，由于被积函数是处处连续的，所以可以在积分号下求导数.

根据引理1可得

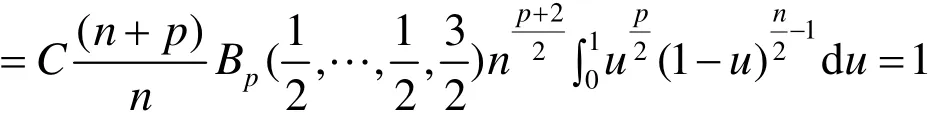
定理3 X ～ Tp(n), f ( x)是X的密度函数，则当n®¥时，有Tp(n)一致渐近正态分布

证明：由于 X ～ Tp(n ) ,g( x)表示度函数，先只需证明当n®¥时，K( f, g ) ®0即

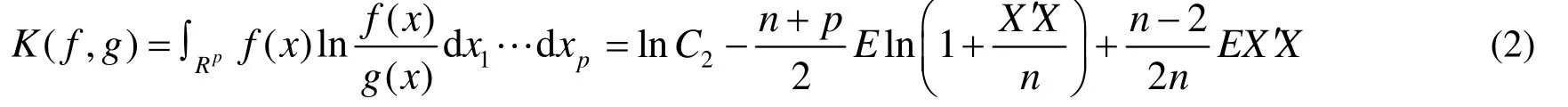
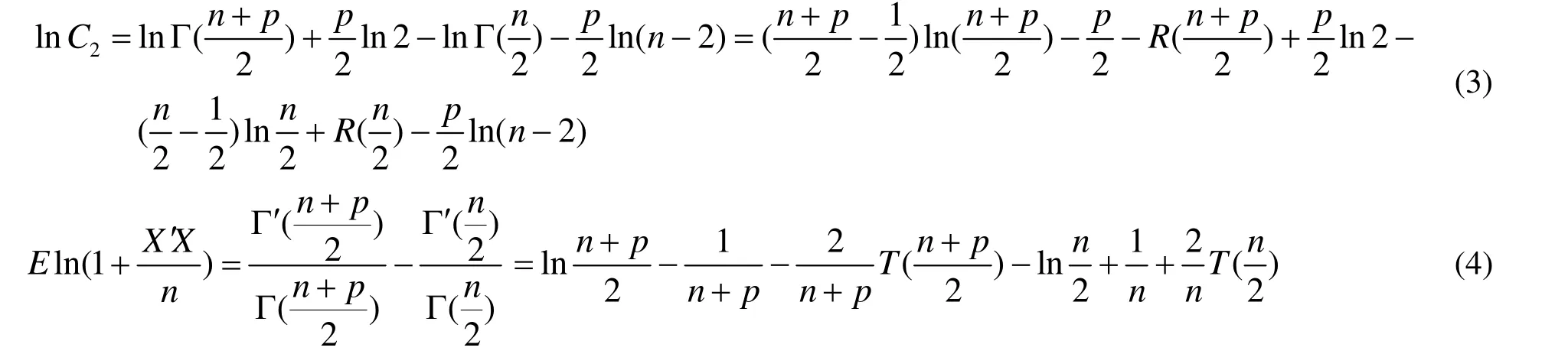
将式(2)(3)带回 K ( f, g)，得

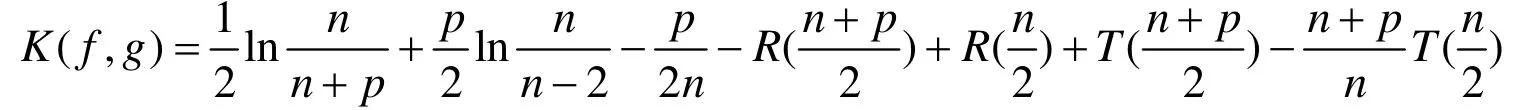
故当n® ¥ 时，T( x) ® 0 ,R( x) ®0，则 K ( f, g ) ® 0 (n ® ¥)， 定理证毕.

本文相当于两个密度函数之间的Kullback-Leibler距离，文中获得了中心多元t分布的一致渐近正态性的条件， X ～ Tp(n)，则当n®¥时，有Tp(n)一致渐近正态分布，但对于非中心多元t分布的一致渐近正态性的条件并未给出证明.

[1] 杨 洁, 李兆庚. 关于多元t分布的极限分布为标准正态分布的证明[J]. 实用化工高等教育学报, 1994, 7(3):78-80.

[2] 李开灿, 孟赵玲. x2分布, t分布, F分布的一致渐近正态性[J]. 北京印刷学院学报, 2004(3): 30-33.

[3] 张光远. 关于多元t分布的一些讨论[J]. 新疆大学学报: 自然科学版, 1996, 13(3): 33-38.

[4] 张荛庭, 方开泰. 多元统计分析引论[M]. 北京: 科学出版社, 1982.

[5] WHITTAKER JOE. Graphical Models in Applied Multivariate Statistics[M]. Chichester: Wiley, 1990.

[6] MATSUNAWA T. Some inequalities based on factorial series[J]. Ann. Inst. Statist. Math., 1976, 28: 291-305.

[7] MATSUNAWA T. On the Stirling Formula [J]. Proc. Inst. Statist. Math., 1978, 25:107-116

[8] 中山大学数学力学系《概率论及数理统计》编写小组. 概率论及数理统计[M]. 北京: 人民教育出版社, 1983.

[9] 李开灿. 矩阵Gamma分布的一致渐近正态性[J]. 数学学报, 2006, 49(2): 435-442.

[10] 方开泰. 实用多元统计方法[M]. 上海: 华东师大出版社, 1989.