简单教数学的三种策略
叶建云
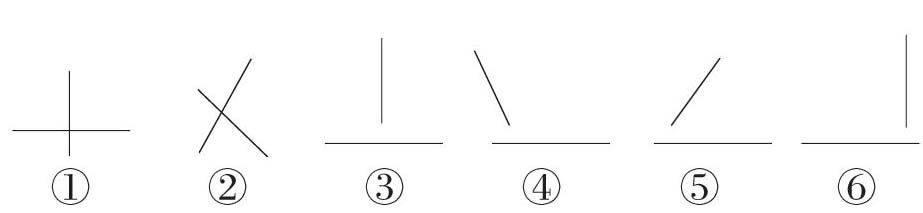
简单教数学是一种教学思想,是一种教学方式,更是一种教学策略。
一、简约而有效的课堂
在课堂教学中,需要我们通过科学、有序、简约的教学活动,让知识背景、智力水平、个性品质等有所差异的学生真正在学习中“人人都能获得良好的数学教育”,实现“不同的人在数学上得到不同的发展”。
1.时间不浪费。一节课的时间只有短短40分钟,每一分钟都是非常宝贵的。我们追求简单教数学,一定要有非常强的时间观念,努力做到:不该浪费的时间,一分钟都不能浪费;探究所需要的,则一定要给足时间。
2.主线要明晰。好课如歌,需要主旋律;好课如河,需要主渠道。我们每一节数学课,都要有明晰的教学主线,即教学的主干脉络。就像“9加几”与“8加几”中的“凑十法”,平行四边形、三角形、梯形等平面图形面积计算学习中的“转化法”,都属于这样的教学主线。有时,一节课的教学主线可能不止一条,教师要学会科学处理。例如,“体积与容积”(北师大版五下),要学习的知识点有两个:一个是“体积”,一个是“容积”。教学时,我们采用一明一暗(或一主一辅)来处理:教师重点组织好“体积”概念的教学,而“容积”的学习,则放手给予学生尝试探索与交流的机会,收到较好的效果。在教学过程中,教师要始终抓住“主线”展开,环环相扣、层层深入,让教学自然、流畅、生动而明快,从中实现有效的教学。
3.素材宜精选。教学如烹饪,没有好的食材,是不可能烹饪出精妙的美食。华应龙老师教学“角的度量”时引用滑梯的“角度”;黄爱华老师在不同的地方教学“百分数的认识”时,分别引用过股票涨跌、绍兴黄酒、足球比赛的控球队时间等例子,堪称精选教学素材的典范。
4.重点需把握。教学重点如何有效把握?要看具体的教学内容而定。李一鸣老师在指导青年教师教学“中位数与众数”时,通过探讨小灰灰的成绩能否算中上水平,将教学重点放在“中位数”概念的引入上,颇具匠心。李老师还在指导另一位青年教师执教“什么是面积”时,全面放手,让学生用自己喜欢的方式自主学习、交流与展示“什么是面积”,有的学生出示一幅中国地图,先用手描出地图边沿,指出“这是周长”,又用手在地图里面涂颜色并指出“这是面积”,多好!这样的教学,重点的把握已在其中。
5.难点求突破。谁都知道,教学要突破难点,可在具体的教学中如何突破呢?请看王栋昌老师教学“相交与垂直”(北师大版四上)一课的教学片段。
师:两条直线相交有几种情况呢?请同学们用两支铅笔当作两条直线摆一摆,并把两条直线相交的各种情况画在课堂练习本上。没听清楚要求的同学可以看屏幕。(课件要求:摆一摆、画一画,用两支铅笔分别代表两条直线,摆出各种相交的情况,并在课堂练习本上画出来)
学生各自比划一段时间后,教师请几位同学到讲台前把相交的不同情况用铅笔摆给其他学生看,之后教师出示相交的六种情况如下图所示。
师:老师根据刚才同学们说到的几种情况,画了六种相交图给大家看,仔细观察,你画的有几种与老师画的是一样的?
生:(略)。
师:请同学们把这六种相交情况按照一定的标准进行分类,看看可以分成几类?
……
铅笔是学生最为熟悉的学习用品。王老师用两支铅笔,便开启了全新视界的探索之旅,突破了教学难点:学生在用两支铅笔“摆一摆、画一画”的过程中,就是在寻找、发现两条直线相交的各种可能的过程。王老师巧用的这一资源简洁、实用,方法指导得当——用课件提醒学生“用两支铅笔分别代表两条直线,摆出各种相交的情况,并在课堂练习本上分别画出来”,学生较快地发现了相交的不同情况。在这基础上,教师接着出示相交的六种代表性情况,“请同学们把这六种相交情况按照一定的标准进行分类,看看可以分成几类”,学生结合自己的想法展开“分类”的探索,教学水到渠成。
二、理性把握
教育是什么?数学教育的最终目标是什么?美国教育家M.克莱因认为:“在最广泛的意义上说,数学是一种精神,一种理性的精神”,数学教育是“教育人们去进行抽象的推理和激发人们对理想与美的追求”。这种“抽象的推理”在早期阶段往往是从人们的生活与社会现实素材中联结与提炼而成的。英国著名教育家洛克在《教育漫话》中指出:“导师应该记住,他的工作不是要把世上可以知道的东西全部教给学生,而在于使学生爱好知识、尊重知识;在使学生采用正当的方法去求知,去改进他自己;通过创造性的方法经历发现的过程,这是学习中最有价值的东西。”
在教学减法简便算法时(一个数减接近整百数的简便算法),形如算式“300-198”,许多学生会出现“300-198=300-200-2=100-2=98”这样的错误,教学效果不太理想。后来,笔者创设了这样的体验情境:“叶老师的孩子长大了,想买一部童车,老师看中了某某商场(在学校附近,学生也比较熟悉)的这辆童车(展示童车图片,并显出价格:198元)。叶老师口袋里没有零钱,只有300元整,怎么办?”学生们开始出招了,有的说:“老师,没有零钱没关系,您就直接给售货员300元钱让找就行了。”有的说:“老师,不用给售货员那么多,给他200元,让他找你2元钱就可以了。”“那老师买童车后还剩多少钱呢?”笔者顺水推舟,让学生进行模拟现场买卖,共同分析其中的数学道理。笔者还和学生共同还原、分析“300-198=300-200-2=100-2=98”的错误情境——买一部198元的童车,先给售货员200元,再给售货员2元。学生们在笑声中掌握知识,学习效果较好。“买”了一部童车,就让学生理解了这类易混易错的知识,这或许就是理性与智慧的魅力吧!
三、适度训练
近来,好像很少有人再提“训练”“练习”之类的字眼了,似乎一提这些字眼,就会与应试教育、落后的教育理念挂钩。邱学华老师曾提出:“教师控制讲话时间,多留练习时间”“及时反馈纠正,练习当堂处理”。我觉得,这些理念永远也不会过时!任何知识与技能,经历过适度的训练,肯定会掌握得牢固些,肯定会不容易遗忘,这是常识。我们追求简单教数学,提倡在教学过程中,重视在课堂中引导学生适度训练(包括课堂练习),精选训练素材,适当完成一些基础题(与例题难度相仿)、提高题(一题多练、一题多变、一题多解、多题比较、多题相融)和创新题(有一定的难度,要让学优生吃得饱)。
这里特别需要指出的是,一个学生的计算能力掌握情况,是学生今后进一步学习数学的重要技能与基础。笔者曾经对近百位初中教师做过一个“关于当前小学生数学能力缺失问题的调查”,其中,83%的教师认为学生小学毕业时计算能力不过关,75%的教师认为学生不懂得做笔记。这些,值得我们小学数学教师思考。其实,小学生计算能力的培养,是最需要进行适度训练的。例如,小学低年级,可以重点训练20以内的进(退)位加(减)法、表内乘(除)法。又如,小学高年级,学生应当熟悉、甚至熟记分母在100以内常用的分数与小数的互化等。
(作者单位:广东省深圳市宝安区官田学校)

