《方程的意义》教学设计

王逸卿 曹炯

教学内容

人教版小学数学五年级上册第53、54页。

教学目标

1.建立方程的概念，并能在提供的式子中正确区分出方程。

2.在等量关系的分析中，从本质上理解方程的意义。

3.在列方程的过程中，初步体会到顺向思维的优势。

教学过程

一、 课前导入

同学们，前几节课，我们已经学习了《用字母表示数》的内容。这节课，老师和大家继续来研究和未知数有关的问题。

二、 建立方程的概念

1.填写含有字母的式子：

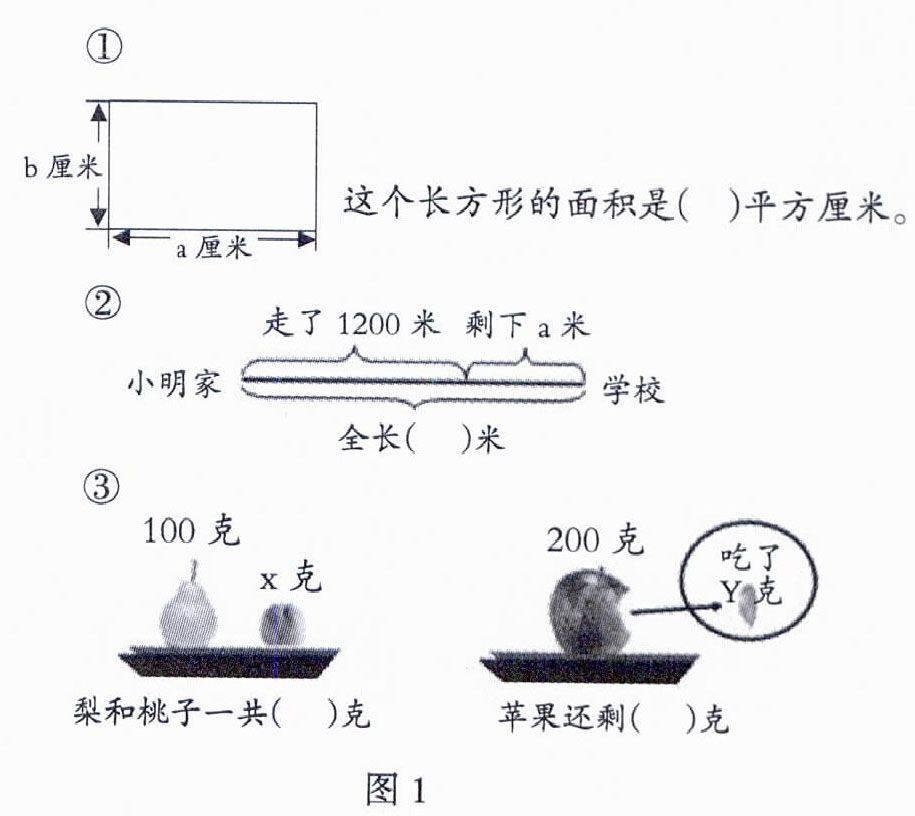
（1）逐一出示3道题目（图1）：请同学们静静地看题，想一想，括号里应该填怎样的式子？

（2）请把式子写在练习纸上。

（3）逐一反馈，教师板书。

ab 1200+a 100+X 200-Y

2.列出相等的式子：

（1）老师告诉大家，这个长方形的面积是24平方厘米。现在，你想到了什么？（板书：a×b=24）

“a×b=24”的理由是什么？（长×宽=长方形的面积）

（2）老师告诉大家，小明家到学校全长1650米，你又想到了什么？（板书：1200+a=1650）

“1200+a=1650”理由是什么？（走了的路程+剩下的路程=全长）

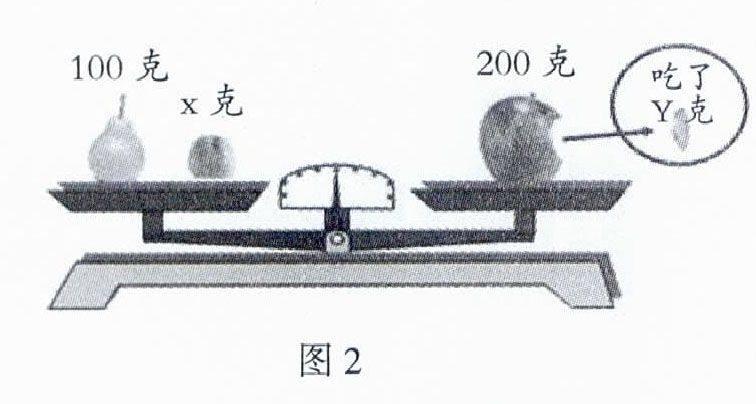
（3）看到天平，你想到了什么？（把第3题的两个盘子组合成一个天平，如图2）

想一想，可以列出怎样的式子？

（板书：100+ⅹ=200-Y）

“100+ⅹ=200-Y” 理由是什么？

（梨+桃子的质量=苹果剩下的质量）

设计意图：在复习中导入，与前面所学的“用字母表示数”自然衔接。同时，改变了单一的“根据天平的平衡情况”来引入方程的方法，采用在表示面积、路程、平衡情况等多个情境中抽象出方程，让学生充分体会到方程是普遍适用于未知和已知之间的等式关系。

3. 建立方程的概念：

（1）同学们，黑板上的3个式子a×b=24 、1200+a=1650、100+ⅹ=200-Y有一个共同的名称：方程。揭题：方程的意义（板书）。

（2）静静地观察，你发现这3个式子有什么相同的地方？

（板书：含有未知数的等式称为方程。）

（3）辨析：你觉得下列哪一个式子不是方程？

35+65=100 x-14>72

y+24 5x+32=47

28<16+14 6（a+2）=42

追问：为什么不是方程？（方程都是等式，等式不一定是方程； 方程含有未知数，有未知数不一定是方程。）

设计意图：在比较与辨析中初步感知方程的意义，能够从形式上区分出方程，但不过分强调形式上的定义。

三、 根据情境列方程

1.看图写方程：

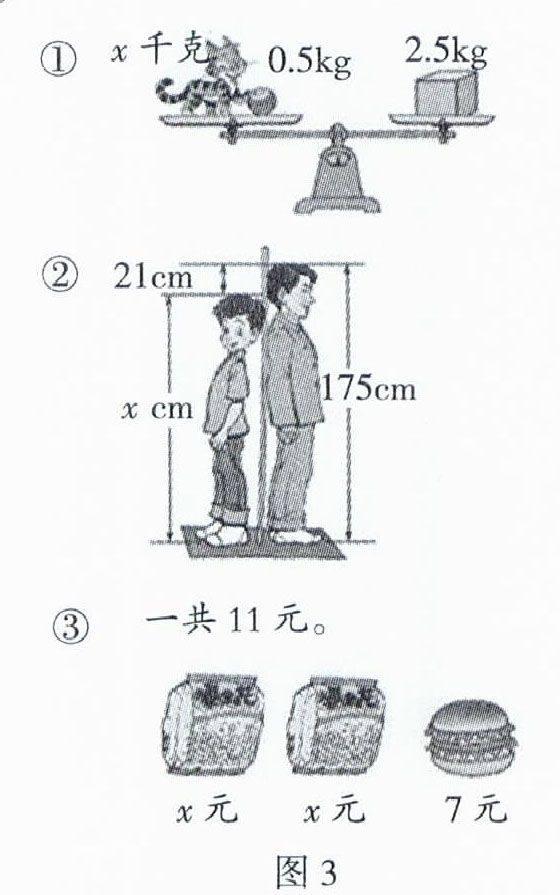
（1）同学们，老师的练习纸上有3幅图（图3），请你在每幅图形中找出一个相等关系，并根据这个相等关系列出方程。

（2）学生尝试。

（3）反馈多份作业：

①展示一名学生的方程：x+0.5=2.5

你找到了哪个相等关系？

②展示一名学生的方程：x+21=175

找到了哪个相等关系？

如有展示：175-x=21可以吗？

175-21= x有什么不一样？

（未知数“X”在单独一边，已经可以直接算出来了，我们一般不列这样的方程。）

③展示一名学生的方程：2x+7=11

猜一猜他找到了哪个相等关系？

如有展示：x+x+7=11 可以吗？ 11-2x=7可以吗？x2+7=11可以吗？

2.看图说方程：

（1）说一说：你能列出怎样的方程？

（2）这样列，你找到了哪个相等关系？

重点反馈：

X+28=40

3X=36

7s=2.8

设计意图：借助直观图形和文字叙述，先让学生尝试寻找等量关系，引导学生对相等关系的关注和表达。强化方程是在未知和已知之间建立的一种等式关系，淡化从形式上理解方程。同时，在反馈的过程中，重点反馈顺向思考的方程，让学生逐步体会到用方程解题是改变了解题的思路，可以化逆向思维为顺向思维，而不是追求方程的多样化。

四、 根据方程找情境

1.根据方程选择情境。

王老师也列了3个方程，请你猜一猜我想到的是什么？

（1）x-17=25

一辆公共汽车上原来有x人，到站后有17人上车。汽车上现在有25人。

一辆公共汽车上原来有x人，到站后有17人下车。汽车上现在有25人。

我想到了哪句话？

为什么是第二句？

第一句话可以列出怎样的方程？

（2）a+3=12

我是根据哪幅图列的？

为什么是左边这幅图？

右边这幅图可以列出怎样的方程？

（3）6M=30

1.每辆小汽车m元，6俩这样的小汽车一共30元。

2.每辆小汽车6元，m俩这样的小汽车一共30元。

我是根据哪句话列的？

为什么两句话都是可以的？

2.根据方程想象情境。

（1）ⅹ+22=40，这一题我还没有想好？这个方程可以表示我们生活中的哪些情况？

先想一想，想到的同学跟同桌说一说！（同桌互说。）

（2）交流： 你帮老师想到了哪些情况？

设计意图：意义的理解不仅需要学生能够从具体情境中抽象出方程，而且需要学生看到方程以后能够想象出具体的情境。在“具体情境和数学抽象”之间来回穿梭，在不断的转译过程中真正理解方程的意义。同时，继续重点反馈顺向思考的方程，进一步体会到方程可以化逆向思维为顺向思维。

五、 介绍关于方程的史料

早在三千六百多年前，埃及人就会用方程解决问题了。在我国古代，大约两千年前成书的《九章算术》中，就记载了一组用方程解决实际问题的史料。

三百年前，法国数学家笛卡尔第一个提倡用X、Y、Z 等字母代表未知数，才形成了现在的方程。这个法国人很厉害，你以后会逐渐发现我们现在已经习惯用这些字母来表示未知数了。

设计意图：简单了解方程的历史，拓展学生对方程的认识，在一定程度上让学生对这位新朋友更为关注，产生更为浓厚的兴趣。

六、 课堂作业

同学们，这节课我们初步认识了方程，下面，我们通过一些练习来回顾这节课所学：

练习一：下面哪些式子是方程？

①x+3.6=7 ②a×2<2.4 ③3-1.4=1.6

④3÷b ⑤8-x=2 ⑥6.2÷2>3

⑦5y=15 ⑧4×2.4=9.6 ⑨2x+3y=9

练习二：列方程。

1.小星骑自行车，每分钟行150米，行了x分，路程是2250米。

2.五（1）班女生有x人，男生比女生多2人，全班一共36人。

设计意图：安排2个练习，通过找方程和列方程，在练习中从形式上再次区分出方程，从本质上进一步理解方程。

七、 课堂小结

同学们，这节课我们认识了方程，你有哪些新的收获？

对于方程的了解我们才刚刚开始，接下来我们会进一步学习方程，学会解方程，你会慢慢体会到方程在解决问题中的作用。