如何证明初中几何题

白海涛

[摘 要]：初中生拿到几何题感觉无从下手，不会分析，没有思路，本文就如何证明几何题阐述一下简单的常用方法

[关键词]：初中 几何题 方法

很多初中学生刚刚接触证明几何题，虽说对于定义，公理和定理能勉强记住，但遇到证明题时却感到无从下手，往往拿到了一个题目就想证，接着是毫无头绪地乱想一阵，容易的题目还能侥幸想得出来，稍难一点的题目就要束手无策了。出现这样问题的原因与学生证明前的准备不足有关，证题前必须仔细读题，明白题中所有名词的定义，完全理解题意，然后分辨出题中哪一部分是题设，哪一部分是结论，若原题无图，则根据题意画好符合题意的图，并标注相应字母，这样才算完成了基本准备工作，下面的任务是着手研究怎样着手证明初中几何题了。

当同学们拿到了一道证明题，而且也做好证题前的一切准备工作，这时就可以开始研究证明的方法思路了。说到怎样着手证明，决不像我们的算术有一定法则或代数有刻板的公式，必须掌握思索问题的方法，逐步去推测、探究，最普通的思索方法就是像医生给病人诊断病因一样，必须先查明病人的症状，然后去研究造成这样的症状的原因，可能是哪几种？再就患病的经过和病人的环境来考察，在这几种可能的原因中决定是哪一种，假使已经断定病人的病症是从饮食不慎而引起的，接着就要研究这病是在胃里呢？还是在肠里呢？不是在其它的器官里呢？于是再去找寻证据，就许多可能的情况分别探究，像这样，从病人的症状出发，去追求造成症状的原因这所在，再逐步分析研究，直到同呈现的一切事项完全符合而止。这种方法通常称为分析法。

在证明几何题的时候，分析法是我们常用的方法，它的步骤同医生的探索病因几乎没有什么两样。我们先从题目结论着想，推测它可以成立的条件，然后就这些重要条件分析研究，看它们的成立必须具备什么条件，这样逐步逆推，直到所需的条件同题目中的已知事项符合而止。

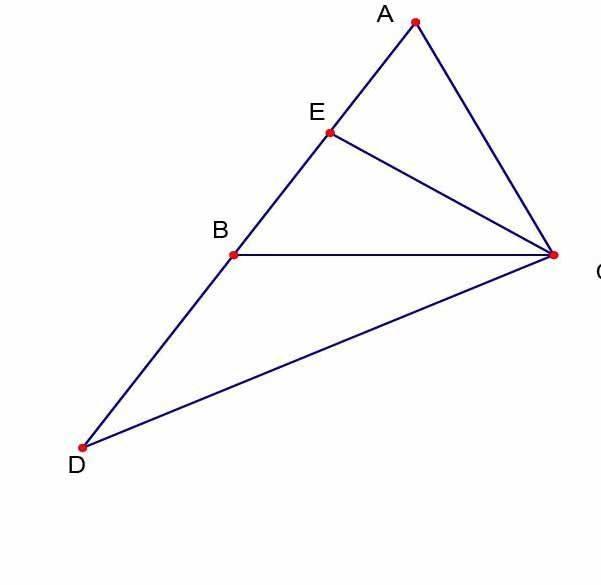
下面就是一个用分析法证明的例题，已知等腰三角形ABC的底边是BC，延长一腰AB到D，使BD等于其腰，又取AB的中点E，求证：CD=2CE

分析：

① 要使CD=2CE成立，必须满足

下列的两个条件之一：

a.CD的一半长等于CE

b.CE的二倍长等于CD

② 假如使用①中的a，要使 ? CD=CE成立，须平分CD于F，下面再研究是否符合下列的条件之一：

a.CF=CE

b.DF=CE

③ 假如使用②中的a，要使CF=CE成立，又须符合下列许多条件之一：

a.CF和CE是一对全等三角形的对应边；

b.CF和CE各等于另一线段。

④ 假如使用③中的a，须连BF两点，使△BCF≌△BCE成立，又须符合下列各条件之一：

a. BF=BE，∠2=∠1，BC=BC（即SAS）

b. ∠2=∠1，BC=BC，∠BCF=∠BCE（即ASA）

⑤ 观察④中的a、b .....，我们知道只有a是同题目的已知事项符合的。因为BF是△ADC二边中点的连线，必须等于? AC，又已知AB=AC，BE=? AB，故BF=BE，又因BF必平行于AC，故∠2=∠ACB，△ABC是等腰三角形，故∠1=∠ACB，于是∠2=∠1，至于BC=BC是相等的，故△BCF≌△BCE可以成立，因而CD=2CE也可以成立。

在上面的例中，若改用①b，②b，③b等，也可以推出与已知事项符合，而得到不同的结论。

我们再看一个生活问题，假如老师给一串钥匙，让甲同学去图书馆取一本关于《几何原本》的书，甲同学若对图书馆是不熟悉的，要想打开室门，就要从一串钥匙中逐一尝试，找出一把，然后再找到放教学书的柜子，再逐步尝试找出一把开柜的钥匙，开了门后，又得寻找哪一格是放几何书的，第几本才是《几何原本》，就这样经过了一番周折，才找到了书。这种方法就是上述的分析法。

用这样的方法解决问题，虽然比较繁，但是符合思索的过程，对于不熟悉这一个问题的解决途径的人来说，是十分合适的。假如你对这一个问题已经有了相当的认识，就可以从已知的事项逐步推理，把问题直接解决。假如甲同学把那本书再放回原处，第二次再去取的话，就可以不费周折，立刻取到手了，这样的方法就叫综合法。

在几何证明中由已知事项经过推理得到结论的方法就是综合法。我们把前面的几何例题的分析法倒过来书写，就成了综合法，我们一般是利用分析法分析问题，而用综合法写出证明过程。

分析法和综合法是我们常用的直接的证题方法，但有时我们还要用到间接的方法来证或证的时候还要通过添加辅助线，从而更好地解决几何证明问题。

参考文献：

[1] 《几何定理和证题》许莼舫

[2] 《初中数学教学法》