谈直线与平面垂直判定定理的教学

徐芬

高中数学立体几何新教材体系中，有的概念直接运用公理来定义概念的教学方法，被教材和广大教师所默认。最近，在一堂“直线与平面垂直的判定”公开课后，我们数学教研组对以此课中涉及到的公理定义概念及后续的判定定理的教学问题，进行了研究与讨论，现整理如下，与同行一起探讨。

一、运用公理定义“直线与平面垂直”概念的思考

对于直线与平面垂直定义的教学，大多教师会演示课本上的实例，旗杆与地面的位置关系，让学生观察直立于地面的旗杆及它在地面上的影子。并指出旗杆所在的直线与地面内任意一条过交点的直线垂直（和不过交点的直线也垂直）。

有些教师也会借助于使用多媒体CAI，展示在现实世界中大量存在的直线与平面位置关系中的这种很特殊的情形，对学生增强直观的直线与平面垂直形象课堂容量进行演示。

在教师的诱导下，学生会利用知识的迁移，自然而然联想到平面内两条直线互相垂直和空间两条直线相互垂直的知识，猜想总结出这种特殊位置关系应该称为“直线与平面垂直”关系。此时，有的教师认为下定义的时机已经成熟，或者引导学生自己去给出准确的定义，或者直接给出教材中的概念：“一条直线和平面内的任何一条直线都垂直，我们就说这条直线和这个平面互相垂直”。我们研讨认为这种教学方法有值得思考的地方。

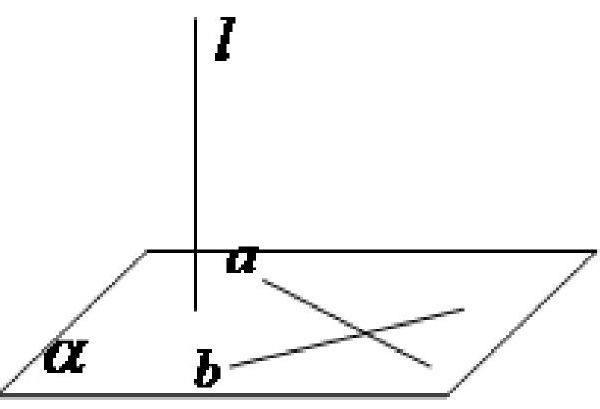
是不是我们一定要用“如果一条直线与平面内的所有直线都垂直则称这条直线与平面垂直”来定义？当然我们也可用“如果一条直线与平面内的两条相交直线垂直，则称这条线与平面垂直”来加以定义（如图）。我们知道，这里的两种不同的条件实际上是等价的，可以互相推出，所以本来这两种选择都可以作为定义的。

既然二种关系原来都可以定义概念，那我们为什么要用第一种方法来定义？

在数学体系中，各个名词是预先已经用公理定义的概念，这样的公理系统是一个实质性公理系统。因为要先定义概念，所以就要有一些原始的概念作为定义其他概念的出发点。一般来说当几种公理都可作为定义某一要领时，特别是有的概念在下定义时，本来就可以有多种选择的情况下，数学体系中往往会把简单的公理留着作为判定定理。比如在初中教材中，平行线的定义与判定定理就是如此。在此，我们就容易理解了数学体系中用第一种方法来定义直线与平面垂直概念，而不是用第二种方法来定义直线与平面垂直概念的理由了。

通过我们以上的教学，让我们的学生知道了“如果一条直线与平面内的所有直线都垂直则称这条直线与平面垂直”与“如果一条直线与平面内的两条相交直线垂直，则称这条线与平面垂直”从本质上来说是等价的道理，为后面的判定定理的学习与运用，埋下了伏笔。

二、从定义引入到判定定理教学的思考

接下来，我们再思考另一个问题，就是在学了“直线与平面垂直定义”后，如何引入“直线与平面垂直的判定定理”的问题？大多教师会按照教材的思路进行这样的引入教学：“要证明一条直线和一个平面垂直，若每次都要证明这条直线和平面上每一条直线都垂直，显然是很麻烦也不必要的”。

这样的引入值得我们教师进行认真的思考了，注意这里教师的引导语“很麻烦也不必要”可能会给学生带来二个误处。

误处一：“很麻烦”导致学生在不善于直接从定义去思考问题，

误处二：“不必要”导致学生误认为遇到有关直线与平面垂直的判定问题时，根本不用去想用定义去证明。

这种误处，学生一旦形成，对所有的定义的理解和运用，特别是对学生的思维活动是非常有害的制约。

实际上，有许许多多的题，完全可以应用定义判定直线与平面垂直，例如：“如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于同一个平面”，既可以用后面的判定定理证明，也可以用定义来证明。我们也可以运用定义来发散思维证题，例如：根据直线与平面垂直的定义，如果平面内存在一条直线与平面的一条交线b不垂直，则可以断定此平面与直线b不垂直。

所以说，定义不是没有用，而是看我们怎么去用。有时用定义去判定比用判定定理更容易解决问题。但大多数情况下，用定义去判定直线与平面垂直确实非常困难，要告诉学生，因为平面内直线的无限性，一条直线与平面内的所有直线都要判定与此垂直，既不现实，也难以操作，所以必须去寻找一种能够避免逐一确定无限条直线与此直线垂直的问题，从而引入到判定定理的教学中。

三、对教材中的判定定理的思考

对直线与平面垂直判定定理，过去大多教师会这样引入：“让我们先来看看木工师傅是如何判断一根立柱是否和板面垂直的方法，用曲尺（注：曲尺，是指木工及钳工常用的一边长一边短的直角尺）检查两次，只要两次，但曲尺靠板面的尺，两次不能在同一条直线上，如果立柱、板面都和曲尺的两条边完全吻合，便可断定立柱和板面垂直。从中你能得到判定直线和平面垂直的方法吗？”引导学生进行猜想推测，从而引入判定定理。

有的教师也会按照教材P65图2.3-4探究的折纸方法引入直线与平面垂直判定定理。但教材也好，老师也好，不管怎么引入判定定理，最后都没有给予确切的严格证明，教材中只提出了二个思考问题作为运用时必须注意的问题——定理中两条相交直线不可忽视（P65），就算把判定定理概念教学告一段落，接下去就直接进行如何运用判定定理了。

这种没有严格证明的“判定定理”，我们认为教材处理不妥会让学生有些迷茫。迷茫有三：

1.我们说，数学中的命题，必须经过严格的证明是正确的，才能成为定理。如果象教材上的实例引入，确实是对的，那也只是是用实验的方法验证了这确实是“正确”的。这种没有经过严格证明的“判定定理”真的是正确的吗？

2.刚刚前面说过，用定义判定直线与平面垂直不现实也难操作，所以要引入容易判定的直线与平面垂直的判定定理，而现在引入了判定定理却又不给证明，这“判定定理”到底是对还是错？

3.教师说，这定理以后可以借助空间向量等方法怎么怎么地来证明，如果以后确实可以证明了，那绕了一大圈，学生会不会说原来也可能是个数学怪圈？是否会产生循环论证之类的错误呢？用今天尚未证明的“判定定理”A推出B，再用B去推出C……，C推出A。

4.就算以后能证明是对的，又有多少学生以后会有这种机会和兴趣去证明？学生此时的知识求知和探索科学的欲望将得不到满足。

我们说，定理包括判定定理，只有从真命题（公理或其他已被证明的定理）出发，经过受逻辑限制的演绎推导，证明为正确的结论的命题或公式，才能成为定理。定理能描述事物之间内在关系，具有内在的严密性，不能存在逻辑矛盾。证明定理是我们数学教学的中心活动，那些相信为真但未被证明的数学只能叙述为猜想，不完全地归纳充其量只能是猜想而非定理。

（责任编辑 易 凡）