初中数学动点问题案例

李小兵

一、教材分析

1.教材教学的背景

初中的教材中并没有对动点问题进行独立的章节介绍，更多的是要依靠学生根据自身已有的知识及对知识的灵活应用的基础上，对相关问题进行思考解决。

2.教材中的地位与作用

动点问题所涉及的知识是相当广泛的，对于不同的知识点都可以衍生出不同类型的动点问题。它对学生的知识水平也是有相对较高的要求，同时对学生的思维有着较高的要求，它体现了学生综合应用知识能力的水平。

3.学情分析

学生在数学相关知识的方面有了一定的积累，也具备了初步的分析问题和解决问题的能力。尽管他们的思维较为活跃，但常常因为综合能力与经验不足，常常出现“无从入手，思维混乱”的情况。

4.教学重难点

教学重点：（1）有条理地寻找符合要求的点。（2）分析动点问题中的线段的数量关系。

教学难点：让学生学会有条理地进行推理，将已有知识应用于实际问题中。

二、目标分析

1.探索动点问题中，如何有条理地寻找出符合要求的点，并能合理地进行解释；掌握解决动点问题的窍门，找出解决问题的突破口，分析条件信息，从而解决此类问题。

2.通过对符合要求的点的寻找，让学生在“动”中找“静”，对运动的点进行探索，培养学生观察、比较、分析、综合、抽象、推理等逻辑思维能力和逆向思维的能力。

三、教学过程分析

1.创设情境，提出问题

师：动点问题是会动的点，这个说法可以，但点是到处跑的吗？举个例子，我们在天空中看到了一架飞机从远方飞了过来，数秒钟后，你能不能再从天空中把它找出来？为什么？

生：可以啊，飞机的飞行路线我们大致是可以判断出来的，所以数秒后，当然可以很快找出它来了。

设计意图：通过学生身边的实例引出学生对于动点问题的兴趣，使学生在动点问题中有更直观的认识，并意识到自己也能行的。

2.师生互动探究新知

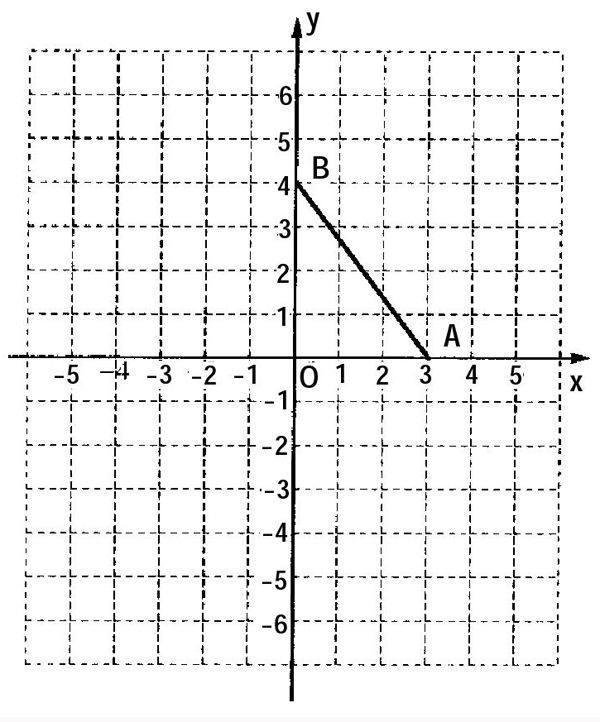
如下图所示，已知，平面直角坐标系上有A、B两点，A点的坐标为（3，0），B点的坐标为（0，4），连结AB，请在坐标轴上找出一个点C，使得△ABC为等腰三角形。符合要求的点有几个？为什么？

解答要点：由水平较低的学生先进行作答，让其有了参与的兴趣，同时也刺激中等以上学生，要努力去思考。最后通过教师的分析，是否以AB为腰，A、B、C三点哪个是顶点，从该点的左右或上下来寻找，让学生在学习过程中体会到什么是分析的合理性、条理性，并由此形成一个良好的分析习惯。

设计意图：分类讨论问题的方法是在动点问题中必不可少的思维模式，只有真正把这个思维方式掌握了，才能真正地、更好地解决动点问题。

3.例题分析

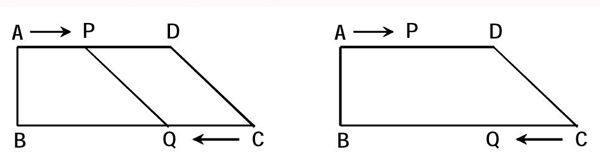
例题：四边形ABCD是直角梯形，∠B=90°，AB=8 cm，AD=24 cm，BC=26 cm，点P从A出发，以1 cm/s速度向D运动，点Q从C同时出发，以3 cm/s速度向B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t（s）。（如下图所示）

分别用含t的式子表示下列线段

AP=_____ PD=_____

BQ=_____ CQ=_____

（1）当t为何值时，四边形PQCD为平行四边形。

（2）当t为何值时，四边形PQCD是等腰梯形。

（3）当t为何值时，PQ=CD。

（4）当t为何值时，QP=QD。

设计意图：此题为常见的双动点问题，在解题过程中，常要涉及相关线段关于时间的代数式。让学生明白，在处理此类问题时，应该将其转化为点的运动路线之间的某种相等关系，从而转化为方程而得解。

4.课堂小结

在师生互动中让学生回顾：

（1）如何寻找具有某种特征的点？

（2）应该如何去解决动点问题？

5.课后作业

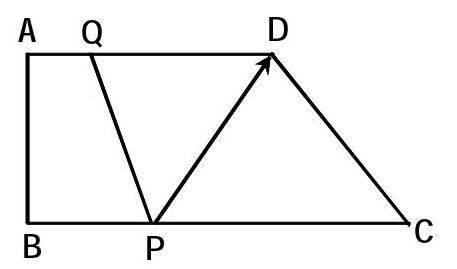
如下图所示，在直角梯形ABCD中，AD//BC，∠A=90°，AB=12，BC=21，AD=16。动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动。设运动的时间为t（s）。

（1）当t为何值时，四边形PCDQ是平行四边形？

（2）分别求出出当t为何值时，①PD=PQ，②DQ=PQ？

四、教法分析

本节采用分组讨论的方法进行教学，目的在于鼓励更多学生参与其中，给他们独立思考的空间。通过简单的题型让大部分学生在讨论的过程中，参与进来，并大胆表达出他们自己的想法，对他们多肯定多鼓励，注重师生间的交流，激发学生学习数学的兴趣，增强解题的信心。

五、评价分析

1.课堂教学应该符合学生的认知规律

本节的内容从简单的知识点导入，让学生在少量的知识基础上便可以进行分析思考，从而不产生抵触的情绪。再由浅入深，将思考的方式、方法应用于稍有难度的题目中，从而解决问题。

2.课堂教学要把教师的主导作用与学生的主体地位有机地结合起来

在教学过程中，教师积极引导学生主动参与，充分发挥学生的主体作用，激发学生的求知欲，从而提高课堂教学效率。

（作者单位 福建省南安市延平中学）