局限于知识传授,还是着力于学生认知需求
杨传冈
一、初教探析:还原数学本质
初教时,我们尝试改变教材的呈现方式,从人数相同与人数不同两个纬度给学生呈现更加真实、有意义、富有挑战性的问题情境。教学预想是第一个情境着重让学生明晰在人数相同的时候,不能仅仅比较个体,应比较总数,如果有学生能说出比较平均数更好;第二个情境试图让学生理解在人数不同的情况下,无论是比较单个个体还是比较总数都显得不够合理,从而希望水到渠成地引入平均数的概念。然而事与愿违,教学现场表明:学生对人数相同这一环节的学习比较顺利,也能一步到位地认识到由于男女生人数不同,单纯比套的总个数是不合理的,但要自然适切地过渡到“求平均每人套中的个数再比较”这一认知内需上是非常困难的。学生在否定了比套中的总数后,想到的是诸如去掉一名女生再比较,或者是挑套中个数最多的学生比较等方法。学生完全把数学生活化了,局限于用生活化的方式解决问题,无法从数据的一般水平这一数学视角进行思考。学生在这个环节上纠缠不清,教师又不敢放手讲解,占用了大量有效教学时间。
磨课时,我们觉得还是应该把落脚点放在学生学习的内在需求上,从学生的认知特点出发,教师精心创设认知矛盾冲突,通过活动对比、启发和诱导,步步为营,不断激发学生对引入平均数概念的强烈认知需求,在丰实的现实情境中初步感知平均数的意义,并将平均数的求法渗透其中。通过动态的“移多补少”演示为进一步理解平均数所具有的“一般水平”“均匀水平”“一组数据的总体情况”等本质特征提供感性支撑,从而凸显平均数的意义。
二、过程重构:顺应认知需求
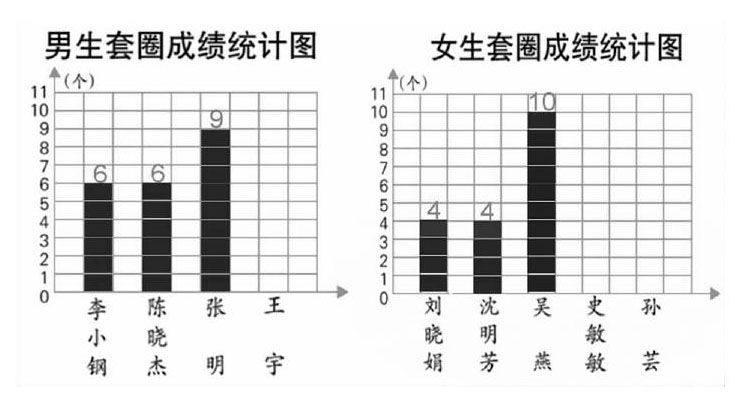
课前组织学生现场进行套圈比赛,记载相关数据。
(一)情景引入、建立感念。
1. 人数相同,个数不同。
师:李小钢第一个出场,他套中了6个。
师:刘晓娟套中了4个。
师:是男生套得准一些还是女生套得准一些呢?
生:6大于4,男生套得准一些。
2. 人数相同,个数相同。
师:(第二个男生6个,第二个女生4个)现在会是男生套得准一些还是女生套得准一些,说说你的想法。
3.人数相同,个数不同。
师:(第三个男生9个,第三个女生10个)现在你觉得是男生套得准一些还是女生套得准一些?
生:比其中一个人,女生最多套中10个,我觉得女生套得准一些。
师:以一个人投中的个数来判断小组的整体水平,合理吗?
生:不合理。
师:有不同想法吗?
生:他们人数一样多,我觉得可以比套中的总数。
生:老师,我同意他的说法,男生套中了6+6+9=21(个),女生套中了4+4+10=18(个),所以男生准一些。
师:当男女生人数相等时(指统计图),我们可以直接比较他们套的总个数。
(二)理解意义,探索求平均数的方法。
1.寻找求平均数的需求(人数不同、每人套中的个数也不同)。
师:比赛结束了,从统计图中你还获得了哪些数学信息?
师:现在,男女生哪一队套得准一些呢?
生:比总数,6+9+7+6=28(个),?摇10+4+7+5+4=30(个)。
师:男生觉得怎么样?这样合理吗?说说理由?
男生:不合理,我们4个人,女生5人,这样比不公平。
师:那单挑比?
生齐:也不公平,刚才就讨论过了。
师:那怎样比呢?
生:可以移一移,使男生每人套中的个数相等,女生每人套中的个数也相等,再比较。
师:多好的办法啊!
师:也就是用男生平均每人套中的个数与女生平均每人套中的个数进行比较。
三、教学反思:站在儿童立场
从学生的视角看来,概念的有效学习需要情和智的二位一体,需要创造一个生动的活动场景激发学习概念的兴趣和热情。课前,教师将套圈游戏搬到了课堂,现场比赛并记录相关数据,唤醒学生既有的比赛公平性生活经验,充分撬动起学生的学习动机。在后续的学习活动中从单人不同数量的比较到双人每组个数相同的比较……巧妙设置矛盾冲突,层层深入、步步紧扣,在跌宕起伏的“男生套得准一些还是女生套得准一些”的不断追问中激发学生探究、破解的积极学习愿望,达到情智的有机融合,实现知识的主动建构。学生在学习概念的过程中需要切身感受到新概念的引入是源自生活的需要,是解决问题的必须。
当下,我们需要自觉站在学生的立场上进行换位思考,尽可能把学习素材与学生原有的认知结构建立实质性、非人为的联系,想方设法找准学生知识学习的起点,让其经历新概念的产生历程,满足认知内在需求,更多地帮助学生积累基本的数学活动经验,激发学生数学活动的原始动力,增强学习的有效性。找准学生已有的认知水平,不仅有助于提高课堂教学的质量,还能有效激发学生的数学学习兴趣,为认知活动提供内在动力。
《义务教育数学课程标准(2011)》将平均数这一学习内容后移至第二学段,要求调整为:体会平均数的作用,能计算平均数,能用自己的语言解释其实际意义。这样的调整显然是关注了教学实践中三年级学生对平均数意义的理解不够到位的客观现实,这也是引起笔者探讨本文的一个重要原因。
(作者单位:江苏省盐城市第二小学 责任编辑:王彬)

