GPS观测数据的仿真＊

周 雨，李英冰

（武汉大学测绘学院，湖北 武汉430079）

0 引 言

仿真GPS观测数据的系统的误差和随机误差都是可以人为控制的，使用的各种模型参数都是精确已知的，使得GPS仿真数据在测试GPS数据解算软件的正确性、基于GPS观测值的定轨方案论证分析、评论各种GPS算法性能等方面，都比实际观测数据更有优势［1－3］。

GPS的仿真数据一般由模拟生成器或仿真软件实现，如GPSLab、瑞士的伯尔尼大学研制的精密GPS定位软件中的GPS仿真模块等［4－6］。但GPS仿真生成器的价格较高，又无法获得其他国外仿真软件的源代码［4］，因此GPS仿真对我们研究卫星导航，如北斗卫星导航定位系统等，都有着非常重要的现实意义。

从单点定位的原理出发，考虑电离层延迟、对流层延迟、卫星钟差、接收机钟差、多路径效应、相对论效应、地球自转改正、测量噪声等影响因素［6－8］，自主设计面向用户的GPS观测值仿真软件，模拟伪距和载波的生成，并以IGS跟踪站的实际观测数据为参考，对模拟值与真实值进行定量比较，并定性的分析出现误差的原因，进一步明确模拟观测的可行性和稳定性。

1 仿真观测值的生成原理

GPS观测值的仿真，是利用用户任意给出的测站三维坐标来模拟该测站观测的GPS信号。GPS卫星发射的信号由载波、测距码和导航电文三部分组成，主要对伪距和载波进行模拟，对他们建立如下的观测方程［7－8，3］。

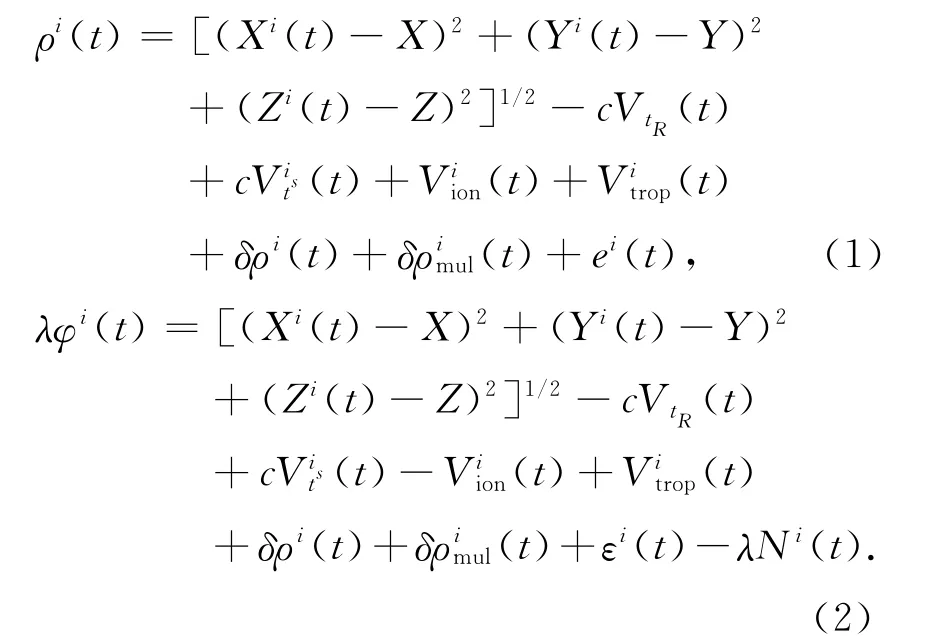
式中：i为卫星编号；t为时刻；ρi为接收机至观测码伪距；XiYiZi为卫星的WGS－84坐标；XYZ为接收机的WGS－84坐标；c为光速；VtR为接收机钟差；为卫星钟差；为电离层延迟改正；为对流层延迟改正；δρi为地球自转改正；δρimul为多路径效应改正；ei，εi分别为观测噪声；λ为相应载波的波长；φi为载波相位观测值；Ni为整周模糊度。

在式（1）、（2）中，卫星坐标XiYiZi和卫星钟差Vits可以根据IGS发布的精密星历进行拉格朗日插值得到，接收机坐标XYZ可以由模拟条件直接给出，电离层延迟改正Viion、对流层延迟改正Vitrop、地球自转改正δρi、多路径效应δρimul可以采用相应模型改正，测量噪声eiεi可以通过随机模型直接生成。

2 仿真观测值软件的设计

GPS观测值仿真的具体过程为：首先，根据模拟的观测时段读取对应的IGS发布的间隔15min的精密星历，并将其进行拉格朗日插值得到与模拟采样率间隔一致的精密星历；其次，从该插值的精密星历文件中获取卫星坐标、卫星速度和卫星钟差，根据卫星坐标与模拟的测站坐标判断卫星的可视情况，并计算出测站到卫星的几何距离；复次，根据模型公式对电离层延迟和对流层延迟进行计算，按照相应模型公式计算地球自转延迟、相对论效应延迟、多路径效应延迟，并对接收机钟差和测量噪声进行随机模拟；再次，将各项延迟改正按照用户需要加入测站到卫星的几何距离中，得到伪距的仿真值，再加入相位观测的初始模糊度和随机周跳值，得到模拟的载波相位观测值；最后将数据按照Rinex文件格式进行整理，生成用户需求的观测值文件。其具体流程图如图1所示，程序的运行的界面如图2所示。

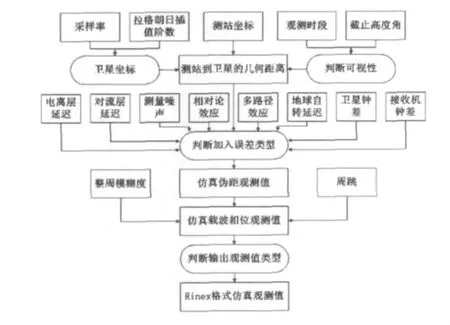
图1 程序的流程图

3 仿真实验与结果

图2 软件运行截图

利用上述的仿真观测软件，选择现有的IGS全球跟踪站作为参考位置，下载实际观测值与仿真观测值进行对比研究。仅选取了上海站（shao）的模拟观测结果与真实观测结果进行对比分析。在整个仿真过程中，参数设置依次为：观测时段为2012年2月10日0时0分至23时59分，采样率为30s，截至高度角为5°，电离层改正采用Klobuchar模型，对流层改正选用Hopfield模型，多路径效应改正、接收机钟差、地球自转改正、相对论效应改正、测量噪声均采用相应的模型。

从图3可以看出虚拟观测到的卫星与实际观测的卫星基本一致，由于虚拟观测设定的截止高度角为5°，与上海站（shao）的实际观测情况有出入，所以出现了部分时段虚拟观测的卫星与实际观测的卫星数不符。图4示出了2号卫星的真实C1、L1、L2值与虚拟C1、L1、L2值的差值，在200个观测历元中，C1差值变化不大且都在0到10 m的范围中，L1和L2差值都在－30周至30周的范围内，基本满足GPS单点定位的精度要求。图5示出了对所有卫星的真实C1值与虚拟C1值的差值统计情况，差值基本出现在0到10m的范围内，仿真的观测值与实际观测值相差不大，主要误差可能是模型改正不精确造成的，还有其他的一些误差可能来自实际观测的外部环境、IGS精密星历文件。

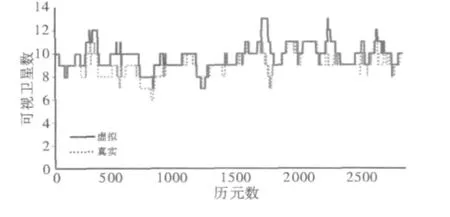
图3 可视卫星总数对比

4 结 论

基于GPS观测值的生成原理，采用面向对象编程方法，开发了GPS观测值的仿真软件，该软件经过初步的试用，得到了较高精度的GPS仿真观测值，基本满足单点定位的精度要求，可以为其他相关科学的研究与应用提供参考。

随着计算机硬件和软件技术的发展，仿真的成本会越来越低，仿真的结果会越来越真实，仿真系统在GNSS导航的各个领域都将有更加广泛的应用。

［1］ 匡翠林，邹 璇，李 陶.利用IGS数据产品进行高精度GPS观测数据仿真［J］.系统仿真学报，2007，19（12）：2857－2859.

［2］ BARTLETT S，LEGRAND R，STATION，E.A－nalysis and simulation of discrete Kalman filtering applied to a GPS receiver［J］.Naval Engineers Journal，1996，108（1）：29－36.

［3］ ELSA M，MAURICIO G，CLAUDIO B.SiGOG：simulated GPS observation generator［J］.GPS Solution，2005（9）：250－254.

［4］ 范国清，王 威，郗晓宁.高精度GPS观测数据的实时仿真研究［J］.国防科技大学学报，31（3）：60－64.

［5］ 郝 明，崔笃信，王庆良，等.高动态GPS观测数据的仿真研究［J］.测绘科学，2008，33（6）：60－62.

［6］ 朱伟刚，陶春燕.GPS观测数据的建模与仿真［J］.海洋测绘，2007，27（5）：26－29.

［7］ 裴 霄，王解先.GPS伪距单点定位的精度分析及改进［J］.海洋测绘，2012，32（1）：5－7.

［8］ 廖 华.GPS伪距单点定位算法的综合比较［J］.测绘科学，2011，36（1）：20－21.