抗野值Kalman滤波在靶场测量数据处理中的应用

周含冰，陈冬冬，彭 燕

（中国洛阳电子装备试验中心，洛阳 471003）

0 引 言

无人机在靶场试验中得到了广泛的应用，承担了越来越多的试验任务。无人机飞行参数的跟踪测量也是靶场测量数据的重要组成部分，飞机测量数据实时处理和事后处理的优劣直接影响到飞机的跟踪测量和控制。然而即使是高精度的测量设备，也会由于各种偶然因素的影响，使测量数据包含1%～2%甚至多达10%～20%的数据点严重偏离真值［1］。这部分异常值即为工程处理中的野值。这些野值会给无人机的状态估计、性能导航及飞行性能分析带来较大的误差，甚至严重偏离实际的飞行状态［2］。因此，必须对这些野值进行辨识和处理，以保证结果的正确性。

目前，对于测量数据的野值剔除方法已经有了大量的研究［1-10］。文献［1］提出了一种野值点的 M型稳健估计统计诊断技术，该方法对孤立型野值和连续型野值都有很好的辨识和剔除效果，但是该方法对于野值点的准确起始位置和结束位置求解不完善。文献［3］把连续5个实测数据的标准差的3倍作为阈值，以此来判定下一个数据点是否为野值，从而完成野值的剔除，该方法对孤立型野值点的剔除有较好的效果，但是不适用于连续型野值的剔除。文献［4］提出了一种利用残差和误差相关矩阵构造二次型作为判定野值的方法，该方法不但可以用于野值的判定，还可用来判定目标运动状态是否发生了改变，但是该方法的数据处理效果与滤波系统的选择有关且只适用于孤立型野值的判别和剔除。文献［5］提出了一种基于模糊预测系统的观测数据野值剔除方法，该方法利用梯度下降法构造最小均方准则下最优的观测序列模糊预测系统，获得预测值和观测值的残差序列，然后基于狄克松准则辨识并剔除观测数据中的野值，该方法适用于孤立型野值的辨识和剔除，且要求2个野值点的间隔必须大于狄克松准则中的序列数，并受初始值和步长的影响较大，误检率也比较高。

文献［6］～［10］研究了各种抗野值kalman滤波算法，这类算法对孤立型野值和连续型野值的辨识都适用，可以有效地识别野值并对其进行修正。

本文通过对新息序列的分析来判断系统测量参数中是否存在野值。当有野值存在的情况下，用一个活化函数加权于新息序列，通过在线修正新息序列，使修正的新息序列能够保持原有的性质，从而消除测量野值对滤波器估计结果的不利影响。仿真结果验证了该方法的有效性。

1 抗野值Kalman滤波

1.1 标准Kalman滤波

考虑线性离散系统，有：

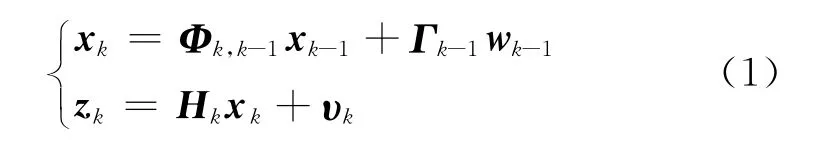
式中：xk为k时刻的状态向量；zk为k时刻的观测向量；Φk，k-1为状态转移矩阵；Γk-1为动态噪声驱动矩阵；Hk为观测矩阵；wk-1和νk分别为系统噪声向量和观测噪声向量，且满足：

式中：Qk为系统噪声的协方差阵，是一个非负定矩阵；Rk为观测噪声的协方差阵，是一个正定矩阵；δkj为Kroneker符号，即：

则Kalman滤波的基本方程为：

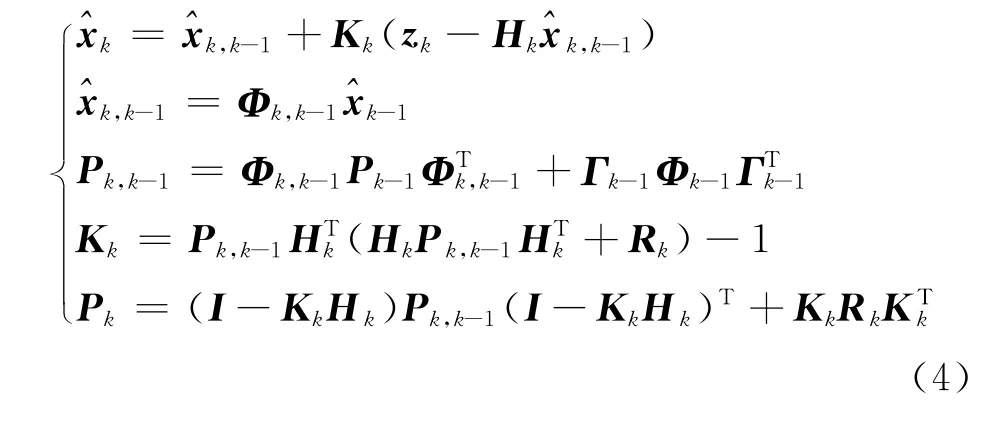
式中：，k-1为状态预测值；Kk为滤波增益矩阵；Pk，k-1和Pk分别为状态预测值和滤波值的协方差矩阵。

给定初始值0和P0后，就可以根据上面的一组公式递推出k时刻的状态向量。

1.2 野值的判别方法

记观测值估计误差为：

式中：ek通常被称为新息。

容易得出，变量rek服从自由度为m的χ2分布，即rek～χ2（m）。rek反映了新息序列的统计特性，而新息序列的统计特性又可反映出观测值的统计特性。故当观测参数中存在野值时，rek的特性也随之发生变化。因此可以通过如下方法判定野值的存在：

式中：α为χ2分布的显著性水平，通常取α＝0.01。

1.3 抗野值Kalman滤波

当判断是否存在野值后，通过对Kalman滤波算法进行修正，提高算法对于观测野值的鲁棒性，减少野值对估计结果的影响：

2．《旧唐书》卷一九二《隐逸·卢鸿一传》:“卢鸿一字浩然，本范阳人，徙家洛阳。少有学业，颇善籀篆楷隶，隐于嵩山。开元初，遣备礼再征不至。”(中华书局1975年版，第5119页)

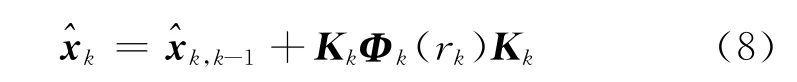
式中：Φk（rk）为活化函数，其取值如下：

由上式可以看出，当判断观测值中不存在野值时，活化函数取单位矩阵，此时即为标准Kalman滤波算法；当判定观测值中包含野值时，活化函数对新息序列进行修正，保证新息序列的特性不变，消除了野值对于滤波估计值的影响。

2 仿真与结果分析

假设飞机相对雷达做匀速直线运动，通过雷达观测数据来确定飞机的位置和速度。考虑到3个坐标分量上的测量误差是互不相关的，而且在3个坐标轴方向目标运动规律也可以看成是相互独立的。故现在以X轴方向为例建立状态方程和观测方程如下：

（1）抗野值Kalman滤波对孤立型野值的抑制效果

在第40s、60s和80s加入野值，仿真结果如图1、图2所示。

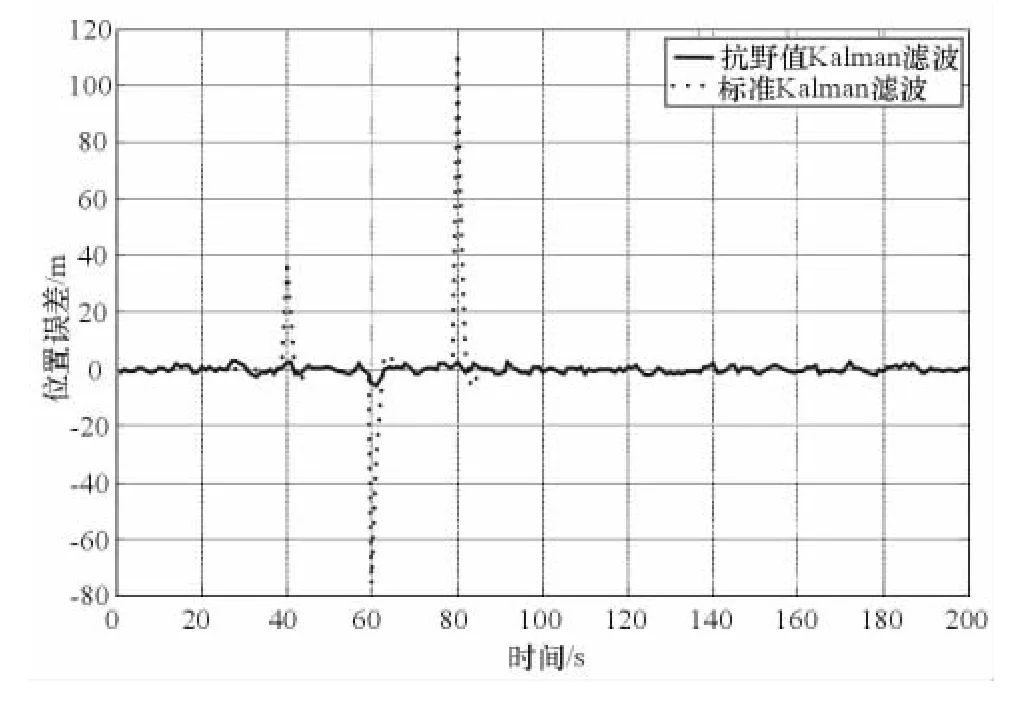
图1 存在孤立野值时2种滤波位置误差

图2 存在孤立野值时2种滤波速度误差

（2）抗野值Kalman滤波对连续型野值的抑制效果

在第40～60s之间，加入标准差为40的野值，仿真结果如图3、图4所示。

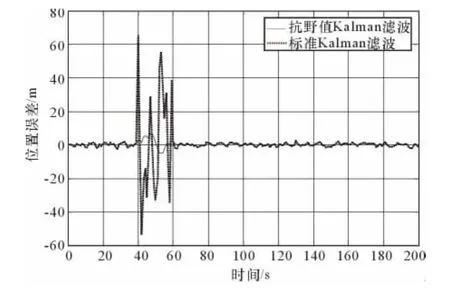
图3 存在连续型野值时2种滤波位置误差

图4 存在连续型野值时2种Kalman滤波速度误差

由仿真结果可以看出，无论是对于孤立型野值和连续型野值，本文的抗野值Kalman滤波能够有效识别出野值并对其进行修正，大大提高了滤波精度。但该方法不适合对机动目标进行跟踪，因为会把目标的机动当作野值对待。

3 结束语

在无人机跟踪测量系统中，如何有效地克服Kalman滤波器在出现野值的情况下引起的发散现象和误差较大严重偏离真值的情况，在工程应用中是非常重要的。

本文所采用的抗野值Kalman滤波，对于在观测值中存在孤立型野值和连续型野值的情况下，均可以克服野值对滤波的不利影响，具有很高的滤波精度，说明该方法具有较强的鲁棒性，是有效可行的。

［1］ 胡绍林，孙国基.靶场外测数据野值点的统计诊断技术［J］.宇航学报，1999，20（2）：68-74.

［2］ 史忠科，王润全.基于飞行运动方程的逐步预测“野值”剔 除 方 法 ［J］.系 统 仿 真 学 报，2010，22（10）：2250-2252.

［3］ 徐利娜，陈俊彪，穆高超.靶场外弹道数据处理中的实时野值剔除算法［J］.应用光学，2012，33（1）：90-95.

［4］ 刘爱东，倪永强，王建国.一种实时提出雷达测量数据中野值的方法分析［J］.火力与指挥控制，2004，29（S1）：17-19.

［5］ 朱学锋，韩荣阁，杨若红.基于模糊预测系统的观测数据野值提出方法［J］.系统工程与电子技术，2006，28（3）：478-482.

［6］ 翟茹玲，柴毅，张可.火箭飞行测控数据野值处理及其无迹 Kalman滤波［J］.计算机工程与应用，2011，47（3）：233-236.

［7］ 卢迪，姚郁，贺风华.一种抗野值的Kalman滤波器［J］.系统仿真学报，2004，16（5）：1027-1029.

［8］ 石静，缪玲娟，倪茂林.一种抗野值自适应滤波算法及在 MEMS-SINS／GPS中应用［J］.宇航学报，2010，31（12）：2711-2716.

［9］ 张帆，卢峥.自适应抗野值Kalman滤波［J］.电机与控制学报，2007，11（2）：188-190.

［10］刘伟，赵伟，刘建业.抗野值自适应Kalman滤波在无人机测风数据处理中的应用［J］.弹箭与制导学报，2011，31（3）：237-240.