基于悲观准则的投掷式雷达干扰战术计算研究

李 宁，钱红军，孟昌盛，付 中

（1.解放军77108部队，成都611233；2.电子工程学院，合肥230037）

0 引 言

战场活动目标侦察雷达是敌步兵、炮兵和装甲部队执行战场侦察任务的主要装备，可引导火力单元实施打击，在战争中对我人员、车辆、坦克以及直升机等低空目标的生存造成极大威胁。此类雷达已广泛采用相控阵体制天线，具有扫描快、波束窄、副瓣电平低、波束驻留时间短［1－2］等战技术特点，只有在活动目标经过的搜索空域内每个波束宽度中至少部署1部干扰机，才能形成对雷达的升空、主瓣干扰，对雷达进行有效压制［3］。

在我低空活动目标实施机动之前，投掷一定数量的有源雷达干扰机，对敌战场活动目标侦察雷达实施干扰，减小其探测距离，降低其探测精度，可以达到掩护我战场低空活动目标的目的。论文以投掷式雷达干扰机掩护圆形等效区域内的活动目标为战术背景，采用悲观准则研究投掷式雷达干扰机的排布方式、投掷位置、投掷时机和使用数量等战术要素的定量计算。

1 问题描述

投掷式雷达干扰机形成矩形干扰屏障，掩护己方活动目标的示意如图1所示，图中以雷达在地面上的投影点O为坐标原点，目标的活动范围为以点O′为圆心、R为半径的圆形区域ΩO，OO′方向为Y轴方向，以竖直向上为Z轴方向建立直角坐标系。活动目标的活动区域与Y轴交于T、T′2点，MN与TT′垂直，｜OO′｜距离为L。

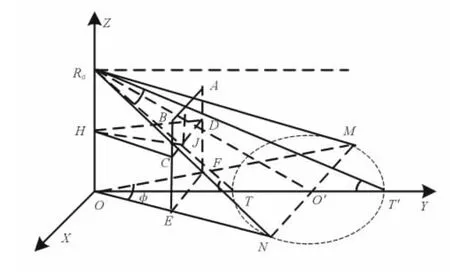
图1 干扰屏障掩护圆形区域内目标示意图

为掩护圆形区域内的活动目标，最保守的方法是从对干扰方最不利的情况出发，如图1所示。计算矩形干扰屏障在目标出现于各种极端位置时的各个战术要素，主要包括：干扰屏障与战场活动目标侦察雷达的水平距离、干扰屏障的水平宽度及竖直高度、干扰机在干扰屏障中水平间隔及竖直间隔和干扰机使用数量。

基于悲观准则的矩形干扰屏障设计思路如下：

（1）当活动目标出现于圆形任务区域与雷达的最近点T时，计算干扰屏障与原点O的距离、干扰屏障的底端高度；

（2）当活动目标出现于圆形任务区域与雷达的最远点T′时，计算干扰屏障的顶端高度；

（3）当活动目标出现于圆形任务区域与雷达在地面投影点O的切点M时，计算干扰屏障底端的一个边界点D的位置；

（4）当活动目标出现于圆形任务区域与雷达在地面投影点O的切点N时，计算干扰屏障底端的另一个边界点C的位置，线段CD的长度｜CD｜即为干扰屏障的长度。

2 干扰屏障掩护方位角、仰角计算

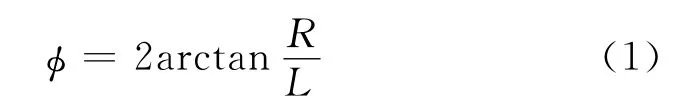
设雷达对T′点探测时的波束俯角为θ1，对T点探测时的波束俯角为θ2，则雷达对活动目标的仰角搜索范围为［－θ2，－θ1］，则：

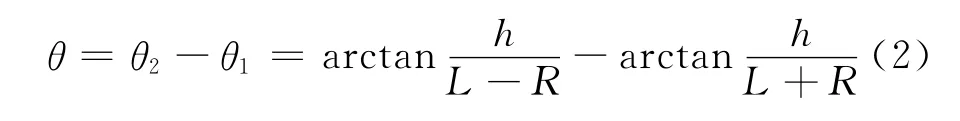
3 干扰屏障与雷达距离计算

以图1掩护区域中距雷达最近的点T作为基准来近似计算主瓣干扰时干扰屏障与雷达的距离，屏障设置与MN平行。当雷达在活动目标位于点T时对其探测，干扰屏障中J处的干扰机对其实施主瓣干扰，忽略其它干扰机的旁瓣干扰功率，由干扰方程可得对雷达实施主瓣干扰的干扰机与雷达的距离Rj应满足方程［4］：

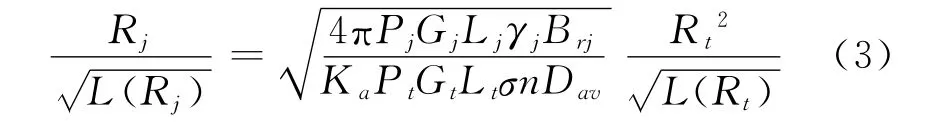
式中：Pj，Pt为雷达干扰机、雷达的发射功率（W）；Lj，Lt为雷达干扰机、雷达的系统损耗（倍）；Gj为雷达干扰机增益和雷达在干扰机方向上的增益（倍）；Gt为雷达发射增益和接收增益（倍）；Brj为干扰功率进入雷达接收机的百分比；γj为干扰信号的极化损失（倍）；σ为目标的雷达反射截面积（m2）；Rj，Rt为雷达与干扰机之间的距离和雷达与目标之间的距离（m）；L（Rj），L（Rt）为与干扰距离、目标距离有关的干扰信号、目标回波信号的大气损耗或其它有耗介质损耗（倍），其中干扰信号为单程损耗、目标回波信号为双程损耗；Ka为对雷达有效干扰时的端内压制系数。

若只考虑雷达信号与干扰信号的自由空间波损耗，则：

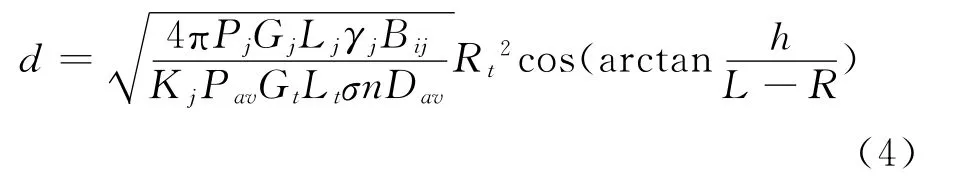
通过求解方程（4）得到此时干扰机与雷达的距离Rj，进而求出干扰屏障距雷达的水平距离：

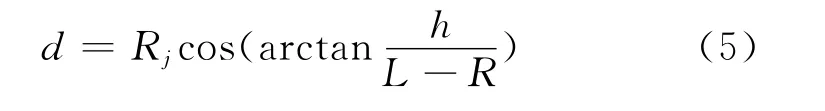
4 雷达干扰机投掷位置计算

4.1 雷达干扰机排布要素计算

干扰地面活动目标侦察雷达时，干扰屏障的水平宽度：

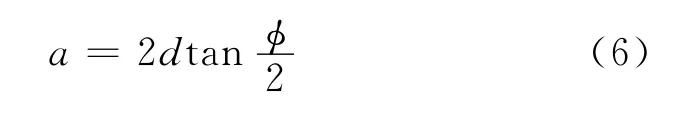
竖直高度：

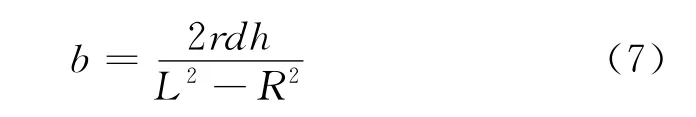
干扰屏障内干扰机的水平间隔：

竖直间隔：

式中：Δφ、Δθ为雷达的水平波束宽度和垂直波束宽度（rad）。

4.2 雷达干扰机投掷位置计算

（1）干扰屏障底端两顶点坐标计算

图1中干扰屏障底端两顶点在地面投影为：

式中：d为干扰屏障与雷达的水平距离（m）。

（2）各部干扰机投掷位置计算

每一批次干扰机的投掷位置和高度均是相同的，设（XC，YC）、（XD，YD）为干扰屏障底端两顶点坐标，M为每批干扰机的数量，则每批干扰机中第i部干扰机的投掷位置坐标为：

式中：i＝1，2，3，…，M。

5 雷达干扰机投掷时间及投掷数量

5.1 雷达干扰机投掷时间计算

雷达干扰屏障在开始干扰前必须形成，故第i（i＝1，2，3，…，P）批干扰机投掷时间为：

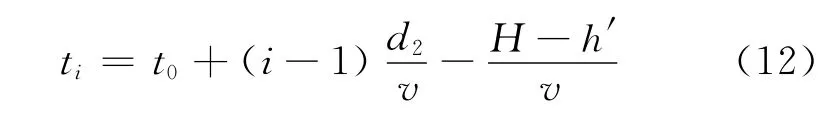
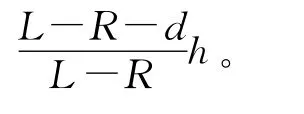
5.2 雷达干扰机投掷数量计算

雷达干扰屏障在任务规定的干扰时间内必须始终保持，故所需干扰机数量为：

6 算例分析

活动目标侦察校射雷达对某一圆形区域内活动目标实施侦察，投掷式雷达干扰机形成矩形干扰屏障，掩护该区域内的活动目标。令可变因素为侦察区域半径r和压制系数Ka，这里侦察区域半径r分别取50、100、200、500、1 000、2 000和3 000，压制系数Ka取5、10、15。表1分别给出了Ka取不同值时，不同r对应的干扰屏障所需干扰机数量N、完成10min干扰任务所需的总数量NA和屏障与雷达的距离l（km）。

通过对表1、表2中所列仿真结果的分析，可以得出以下结论：

表1 干扰屏障所需干扰机数量N、总数量NA和屏障与雷达距离l

表2 干扰屏障顶点A、B、C、D 位置（Ka＝10，β＝0.8）

（1）当r＝0时，N和NA最小；当r逐渐增大时，N和NA随之持续增大。随着压制系数Ka的增大，N不变，NA增大。

（2）压制等级越高，l越小，并且随着压制等级的升高，l减小的幅度会减小，当Ka由10增大到15时，l减小的程度大致是Ka由5增大到10时的一半。

7 结束语

本文针对战场活动目标侦察雷达的相控阵天线特点，采用投掷式干扰方式，以掩护圆形等效区域内活动目标为战术背景，采用悲观准则研究投掷式雷达干扰机的排布方式，投掷位置、投掷时机和使用数量等战术要素的定量计算，对于高效发挥投掷式干扰机的作战效能，有效指导投掷式干扰机的作战运用提供了参考。

［1］田兆春，牛杰.战场侦察雷达装备与应用［M］.沈阳：白山出版社，2002.

［2］张光义，赵玉洁.相控阵雷达技术［M］.北京：电子工业出版社，2006.

［3］沈阳，李修和，陈永光.一种新的压制性干扰技战术研究［J］.电子与信息学报，2008（5）：1068－1071.

［4］淡金强.有源雷达干扰弹干扰效能评估模型研究［J］.指挥控制与仿真，2008（3）：77－80.