基于小波变换的单帧图像分辨率增强方法

冯清枝

（中国刑警学院 辽宁 沈阳 110035）

基于小波变换的单帧图像分辨率增强方法

冯清枝

（中国刑警学院 辽宁 沈阳 110035）

在简要分析图像插值原理、方法和特点的基础上，提出一种将小波变换与混合插值相结合的单帧图像分辨率增强方法，旨在改善涉案图像的视觉效果，为办案人员提供更多的有用信息。实验结果表明，该方法获得的复原图像不仅在主观上增强了原始图像的辨析程度，而且在客观上提高了原始图像的峰值信噪比，能够更准确地反映真实场景。

图像插值 小波变换 混合插值 分辨率增强

1 引言

在案件侦查和诉讼审判等司法活动中，公安、司法机关依法采取先进的影像技术手段，采集、存储和检验一切能够证明案件事实，与案件相关的人、物、环境等客体影像资料。这些影像资料能够形象生动地反映案件事实，再现犯罪过程，成为案件侦查的直接证据。同时，影像资料也具有独特的证明力和其他证据无可替代的优越性，在我国诉讼证据体系中具有独立的证据地位，在司法实践中获得广泛的应用。然而，影像资料在给案件侦破和审理工作提供机遇的同时，也给影像资料检验分析工作带来巨大挑战。事实上，影像资料在形成、传输和记录过程中，由于受到现场环境干扰、影像系统自身缺欠、取证技术手段滞后等因素的制约，使得从影像资料中获取的单帧图像往往达不到理想的分辨率要求，给检验分析工作造成极大的困难。图像插值是增强单帧图像分辨率的唯一方式，能够为办案人员提供更多的有用信息，加快案件侦破和审理工作的进程。

图像插值是一个图像数据再生的过程，在给定的空间范围内，由有限的离散图像数据准确地推算出更多的图像数据，构造出具有更高分辨率的观测图像以反映真实场景。先进的图像插值技术能够有效地增强图像分辨率，广泛应用于卫星遥感、材料分析、医疗诊断、交通管理、刑事侦查等领域。图像插值大体上划分为传统插值方法和现代插值方法两大类。传统插值方法又称为线性插值，是利用图像已知像素点的灰度值与特定的插值基函数之间的二维卷积运算，计算出未知像素点的灰度值，如最近邻域插值、双线性插值、双三次插值、多项式插值和样条插值等算法。传统插值方法对图像的高频信息具有抑制效应，致使复原图像的边缘区域出现模糊或者锯齿现象，对图像的边缘细节和纹理特征的复原效果不够理想。新兴的现代插值方法又称为非线性插值，是将分形拓扑、小波分析、偏微分方程、最优化理论等非线性理论引入数字图像处理中，针对图像的不同区域采用不同的插值方法，并根据图像频谱调节加权系数，建立自适应的空间移变插值算法，以获得更为理想的复原效果，如分形插值、小波插值、偏微分插值、等照度线插值等算法。综合多种图像插值算法的特点，提出一种将小波变换与混合插值相结合的单帧图像分辨率增强方法，用以改善涉案图像的视觉效果。

2 图像的小波分解与重构

小波变换是由法国地球物理学家J.Morlet于1984年对地球物理勘探资料进行分析时提出的。小波变换是一种新的信号分析理论，具有逐渐局部细化和多分辨率分析等特性，并且小波变换的多尺度分解特性更符合人类的视觉机制，成为图像分析和处理的有力工具。1989年S.Mallat受到金字塔算法的启发，从多分辨率分析的角度构造了小波分析的框架，建立了Mallat多分辨率算法，使小波分析取得了突破性进展，由理论研究转向应用开发。

Mallat算法是基于子带滤波器组的正交小波分解与重构算法，可以实现对二维图像进行多分辨率的分解与重构。对于一个二维图像f(x,y)∈L2(R2)来说，其在2j尺度空间的二维离散小波变换为：

式中，ø(·)为尺度函数，ψ(·)为小波函数。若令Hr和Hc分别表示对阵列 cj(m,n{ } )的行与列进行低通滤波运算的系数矩阵，而Gr和Gc分别表示对阵列cj(m,n{ } )的行与列进行高通滤波运算的系数矩阵，则二维图像的Mallat分解算法可以描述为

离散小波变换可以将第j层图像Cj分解为一个低频子带图像Cj+1和三个高频子带图像Dij+1。低频子带反映出图像的背景信息，而高频子带则反映出图像的边缘、轮廓和细节信息，即DVj+1、DHj+1、DDj+1分别反映出图像中垂直方向、水平方向、对角方向的边缘、轮廓和细节信息。而离散小波逆变换又可以将第j+1层低频子带图像Cj+1和高频子带图像Dij+1重新组合成图像Cj，相应的二维图像的Mallat重构算法可以描述为

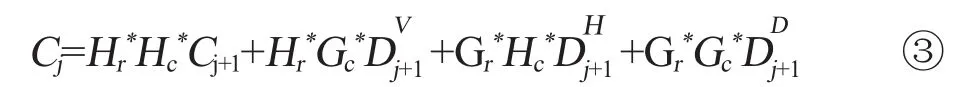
式中，Hr*、Hc*、Cr*、Cc*分别为滤波运算的系数矩阵Hr、Hc、Cr、Cc的共轭转置矩阵。

图像的小波分解与重构过程如图1所示。原始图像经过多级小波分解之后，形成一系列不同尺度、不同方向的子带图像。这些子带图像具有金字塔式分层结构，每一分层子带图像的分辨率不同，分别由一个低频逼近图像和三个高频细节图像组成。这种分层结构，与人眼视觉系统由粗略到精细、由全局到局部观察事物的过程是一致的，并且结合人眼视觉的空间方向特性，实现对原始图像的逐渐局部细化和多分辨率分析。如果不对子带图像进行任何修改的话，那么各个分层子带图像经过多级小波重构之后，将重新合成原始图像。事实上，对子带图像的尺度系数、小波系数的选择编码方式不同，以及子带图像的重构组合方式不同，衍生出不同的基于小波变换的图像处理方法。

图1 图像的小波分解与重构过程

3 图像分辨率增强算法

3.1 小波插值

原始图像经过小波分解后形成一系列子带图像，不同尺度、相同方向的子带图像的相关程度较高，将低分辨率的子带图像通过某种方式近似为高分辨率的子带图像，再经过小波重构便可获得比原始图像具有更高分辨率的观测图像。具体步骤如下：

（1）对原始图像f0进行二维插值，由此获得插值图像f的分辨率为原始图像的二倍；

（2）按照公式②，对插值图像f进行一级小波分解，分别获得一个低频子带图像C1和三个高频子带图像DV、DH、DD；

111

（3）令低频子带图像正比于原始图像，即C′1=α·f0，α为能量调节参数；

（4）按照公式③，对子带图像C1′、D1V、D1H、D1D进行小波重构，获得小波插值图像f′。

3.2 混合插值

双线性插值和双三次插值是两种经典的插值方法，各自具有优缺点。从信号滤波角度来看，双线性插值具有良好的低频响应特性，而双三次插值则具有较好的高频响应能力。因此，将双线性插值和双三次插值的优点相互结合，利用混合迭代运算以获得最佳的图像插值效果。具体步骤如下：

（1）运用双线性插值对原始图像f0进行插值计算，获得插值图像fk-2；

（2）运用双三次插值对原始图像f0进行插值计算，获得插值图像fk-1；

（3）选择混合参数β（0≤β≤1），对两幅插值图像进行加权求和计算，获得插值图像fk；

（4）按照公式④，经过多次迭代运算，获得混合插值图像f′。

迭代运算的结束条件可以由两种方法确定，一是当fk与fk-1之间的均方根误差小于预先设定的阈值时，终止运算；一是当迭代运算的次数等于预先设定的数值时，终止运算。此外，混合参数β的选择与原始图像的复杂程度有关，准确与否将直接影响着图像插值的质量。

3.3 算法设计

图像分辨率增强算法是针对涉案图像分辨率过低、难以识别图像信息而提出的，将小波插值和混合插值进行优化组合，进一步提高图像插值的精确度，克服传统插值方法存在的缺欠，有效地增强图像分辨率。其处理流程如图2所示。

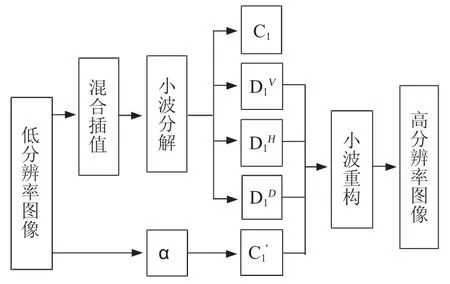
图2 图像分辨率增强算法流程图

4 实验结果及分析

实验检材是嫌疑车辆通过地下停车场出口时由监控摄像机记录的画面。监控现场环境照度较低，光线条件不够理想，加之监控设备性能较差，监控画面的分辨率为320×240像素，致使嫌疑车辆图像质量低劣，缺少必要的特征信息。根据案件侦查工作的需要，从监控画面中截取嫌疑车辆牌照图像，转存为JPEG格式，图像大小为87×74像素，如图3所示。

图3 原始图像（87×74）

图4 双线性插值图像（174×148）

为了便于比较分析，利用MATLAB7.0软件编写图像插值程序，对图3所示的车辆牌照图像进行分辨率增强处理。图4为双线性插值处理结果，尽管图像分辨率得以增强，是图3的二倍，但是插值方法的低频响应特性造成插值图像相对模糊，影响着车辆号牌的识别效果；图5为混合插值处理结果，是将双线性插值与双三次插值相互结合，利用混合迭代运算获得的插值图像，由于没有超出传统插值方法的制约，插值图像的视觉效果改善程度不大；图6为本文提出的算法处理结果，复原图像细节丰富、边缘清晰、没有明显畸变，与其他插值图像比对分析，能够准确地辨认出嫌疑车辆的号牌字符。此外，峰值信噪比是一种与人眼视觉特性比较接近的客观评价标准，通常用来比较原始图像与复原图像之间的视觉质量变化。经过实验测算，双线性插值、混合插值和本文算法的峰值信噪比分别是：32.98dB、33.22dB和34.06dB。

图5 混合插值图像（174×148）

图6 本文算法处理结果

5 结束语

自然景物总是包含无限多的细节，一幅理想图像应当详尽地反映出自然景物在特定的时空条件下的瞬态能量分布，其频谱范围是无限宽的。但是，实际观测图像的频谱范围却是有限的，较多的高频信息在图像获取过程中丢失，因此，观测图像只是理想图像在一定分辨率下的近似。在缺乏必要的先验知识或约束条件的情况下，通过图像分辨率增强方法，由单帧观测图像复原出理想图像是一个典型的病态问题，理论上讲，存在无数的高分辨率复原图像与这一帧低分辨率图像相对应。图像插值是通过引入一些理想化条件缓解单帧图像分辨率增强的病态性以获得唯一解。混合插值是依据最优化理论，通过迭代运算形式逼近理想图像；而小波变换则是将混合插值图像的高频信息与原始图像有机融合，在保证图像真实性的前提下，尽可能地复原图像细节，提高图像的清晰度。从主观视觉效果来看，本文提出的方法能够有效地增强原始图像的分辨率，提高图像判读的准确度。从客观性能指标来看，与其他插值算法相比较，该方法能够明显地提高原始图像的峰值信噪比，改善图像的高频信息，较好地逼近理想图像。当然，在应用图像分辨率增强方法时，需要引入一些参数、阈值等，在一定程度上降低了方法的适应性，因此，智能化的自适应图像分辨率增强方法将是未来的研究方向。

1.Temizel A，VlachosT.Wavelet Domain Image Resolution Enhancement[J].IEEE Trans.on Vision，Image and Signal Processing，2006，153（1）

2.陈武凡.小波分析及其在图像处理中的应用[M].北京：科学出版社，2002

3.冯象初，姜东焕，徐光宝.基于变分和小波变换的图像放大算法[J].计算机学报，2008，31（2）