高温蝶阀阀座温度分布和应力分析

喻九阳，郑 鹏，叶 萌，彭红宇

(武汉工程大学机电工程学院，湖北 武汉 430074)/

0 引 言

蝶阀[1]是用随阀杆转动的圆形蝶板作启闭件、往复回转90℃左右来开启、关闭和调节流体通道的一种阀门，广泛用于冶金、轻工、电力、石油化工系统的煤气管道及水道等，其优点在于：结构简单、体积小、重量轻、耗材省、启闭迅速以及流阻小.国内生产的阀门中，将工作温度t>450 ℃的蝶阀称为高温蝶阀[2].

某公司烟机入口的调节阀采用DN1200电液高温蝶阀，其中，阀体结构为两偏心形式，且阀体与管道采用焊接连接,其结构尺寸图如图1所示.高温蝶阀的操作温度为650 ℃，阀座和阀板的材质为0Cr18Ni9，保温层厚度为80～100 mm，保温材料为防水泡沫石棉.由于操作温度较高，若温度分布不均匀或沿壁厚温度梯度大， 蝶阀就会产生较大的热变形，导致局部伸缩而出现卡死的可能，从而影响生产的正常运行[3].为此，笔者利用ANSYS有限元分析软件对保温层厚度100 mm情况下的高温蝶阀阀座建立了较为精确的三维有限元模型，并进行了工作状态下热应力分析.

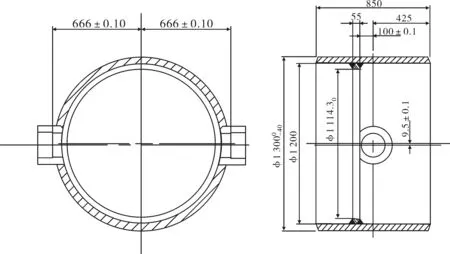
图1 阀座平面尺寸图Fig.1 The plane size chart of valve seat

1 几何模型

利用ANSYS分别建立蝶阀阀座和保温层的几何模型，考虑到两端支撑边界对蝶阀受力情况的影响，这里将两端模型向两端各延长600 mm.其中，各处保温层厚度为100 mm，整体几何模型如图2所示.

图2 整体几何模型Fig.2 The overall geometry model

2 有限单元模型

高温蝶阀阀座以及保温层之热分析采用SOLID70单元[4]，在对阀座以及保温材料采用SOLID70单元划分中，考虑到集合模型的复杂性，若直接采用粗糙四面体网格划分单元，会导致网格严重畸形，直接影响到分析结果的精度；若采用细化的四面体网格，单元数会急剧增加，显著延长计算时间或导致不能计算.为保证网格质量和分析结果的准确性，本文将整体分析模型细分为424个体积块，并依次进行网格划分，确保有限单元网格的光滑过渡，并不产生严重畸形单元.整体有限单元划分模型如图3所示，共24 372个SOLID70单元.

图3 整体有限元模型Fig.3 The whole finite element model

3 蝶阀热分析

3.1计算条件

蝶阀的操作温度为650 ℃，即将其内表面温度设置为650 ℃；保温层与大气层直接接触，并与空气发生对流换热，取保温层外表面的对流换热系数为20 W/(m2·K)，参考温度为25 ℃，另外，考虑到模型两端的连续性，端部设置为绝热条件；蝶阀阀座保温层的材料为防水泡沫石棉[5]，其导热系数为0.033～0.044 W/(m·K)，为保证计算的保守性，取值为0.044 W/(m·K).阀座材质为304不锈钢，不同温度下的导热系数[6]如图4所示，由图4可知，温度对材料导热系数影响很大，且随温度升高而增大.根据蝶阀平均温度为325 ℃时的导热系数进行计算，即在温度为598 K时304不锈钢的导热系数为18 W/(m·K).

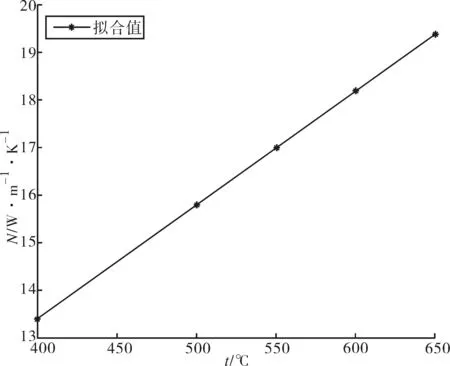
图4 不同温度下304不锈钢的导热系数Fig.4 Thermal conductivity of 304 stainless steel under different temperature

3.2 分析结果

施加初始条件和边界条件后，整体分析模型的温度分布如图5所示，结果表明整体温度沿轴向基本均匀分布.整体模型温度沿厚度方向的分布如图6所示.

图5 整体温度分布Fig.5 The overall temperature distribution

图6 温度沿厚度方向分布Fig.6 The temperature distribution along the thickness direction

图6中横坐标0为阀座筒体的内径处，横坐标50为阀座筒体的外径处(也为保温层筒体的内径)，而横坐标150为保温层筒体的外径处.计算结果表明，阀座筒体的温度沿厚度基本均匀分布，而保温层的温度沿厚度呈线性递减.

由图7可知，阀座筒体温度云图基本一致，而阀座圈处温度变化较大，且沿周向分布不均匀.具体来说，阀座筒体端部处温度沿厚度的分布情况如图8所示，结果表明阀座筒体整体上温度均匀，且沿壁厚温差仅为1 ℃左右； 阀座圈处温度沿厚度的分布情况如图9所示，结果表明阀座圈处沿厚度的温差较大，最大温差约为10 ℃，另外，阀座圈处筒体沿壁厚的温差也略有增加，温差约为2 ℃.

图7 阀座温度分布图Fig.7 The temperature distribution of valve seat

阀座保温层温度分布如图10(a)所示，结果表明保温层选100 mm是合适的，不仅阀座筒体温差非常小(低于1 ℃)，且保温层外表面温度较低.具体而言，保温层温度沿壁厚分布情况如图10(b)所示，结果表明温度沿保温层厚度基本呈线性分布.

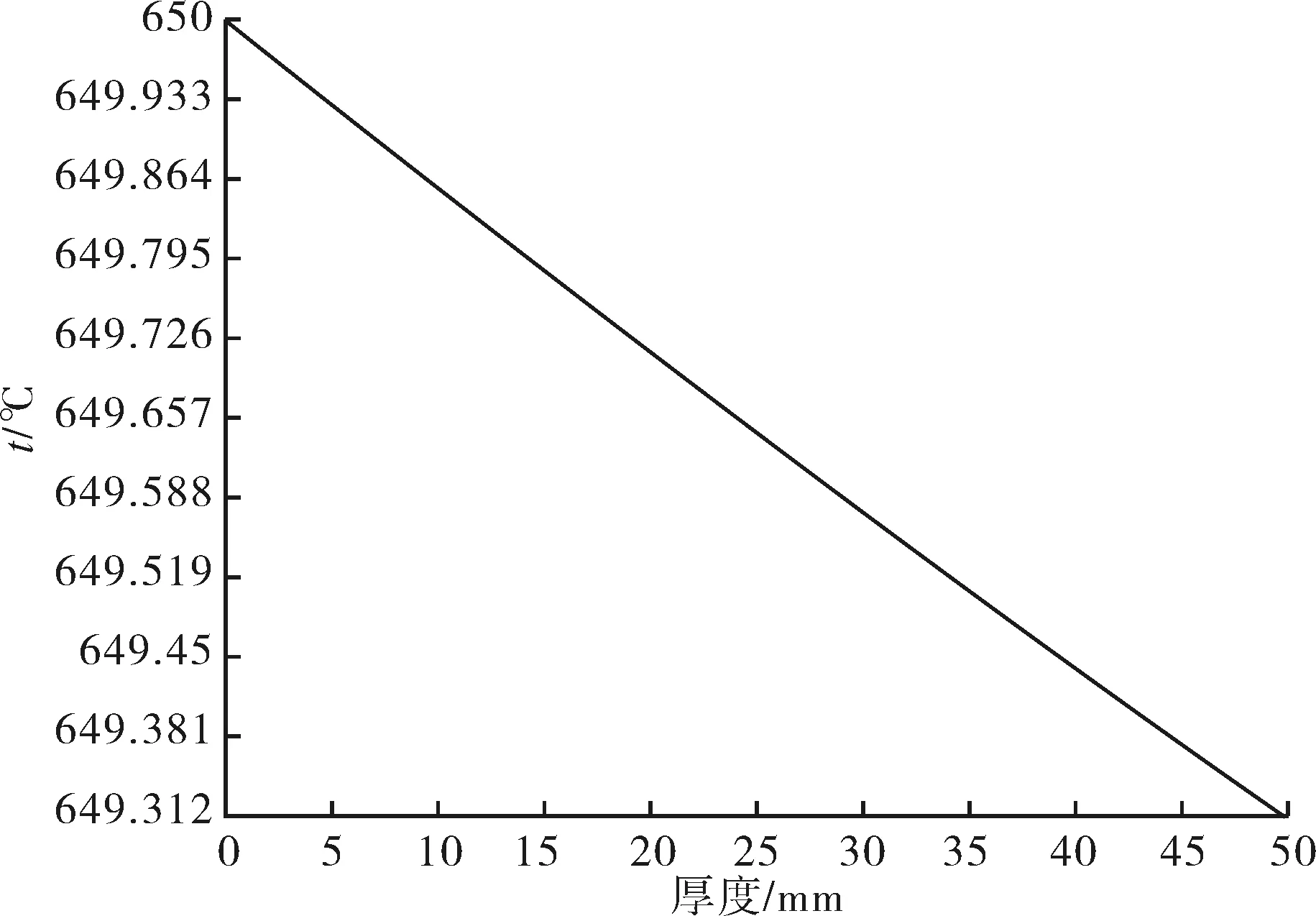
图8 阀座筒体端部处温度沿厚度的分布Fig.8 Temperature distribution along thickness of the end of valve seat tube

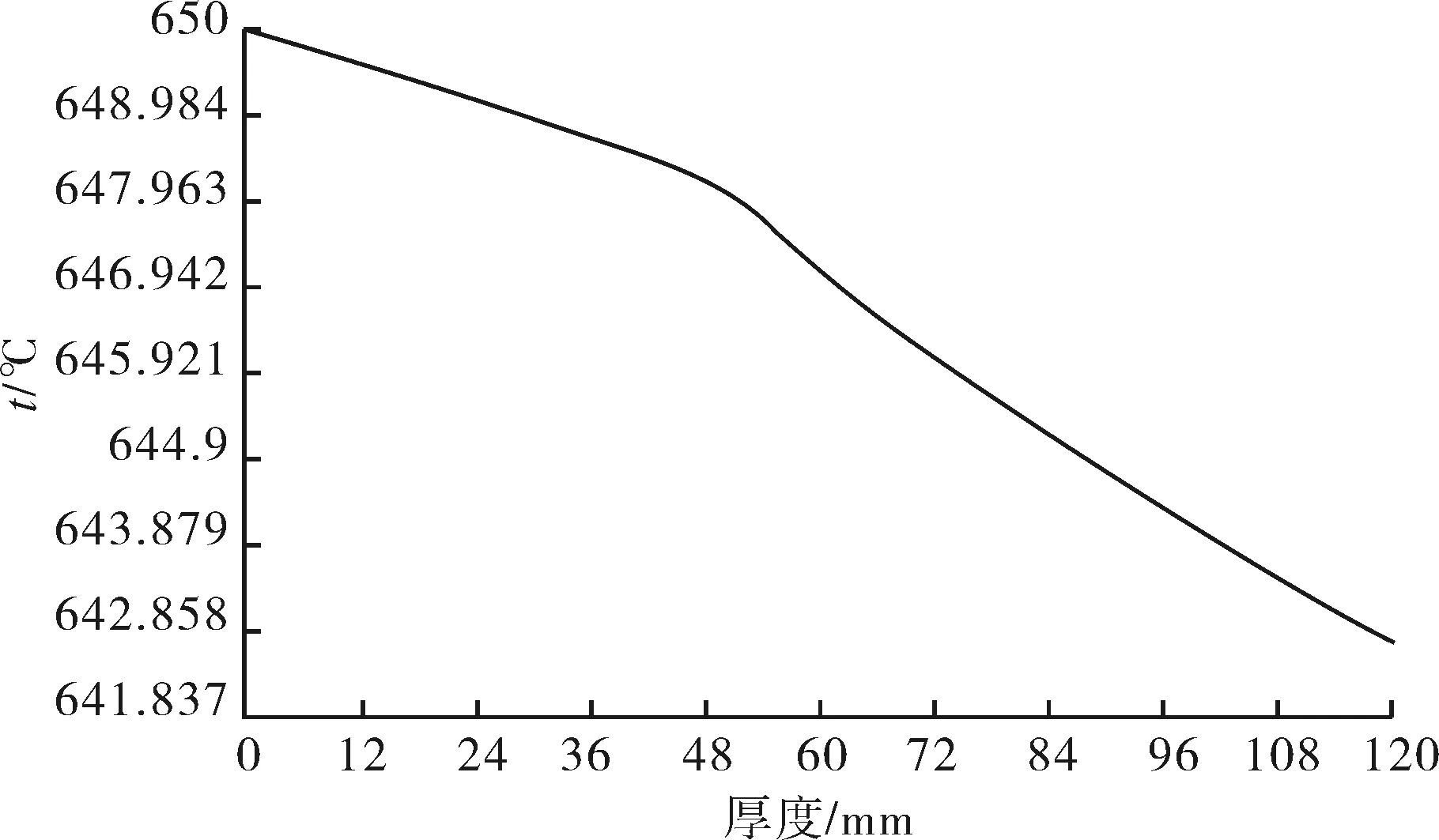
图9 阀座圈处温度沿厚度的分布Fig.9 Temperature distribution along the thickness of valve seat ring

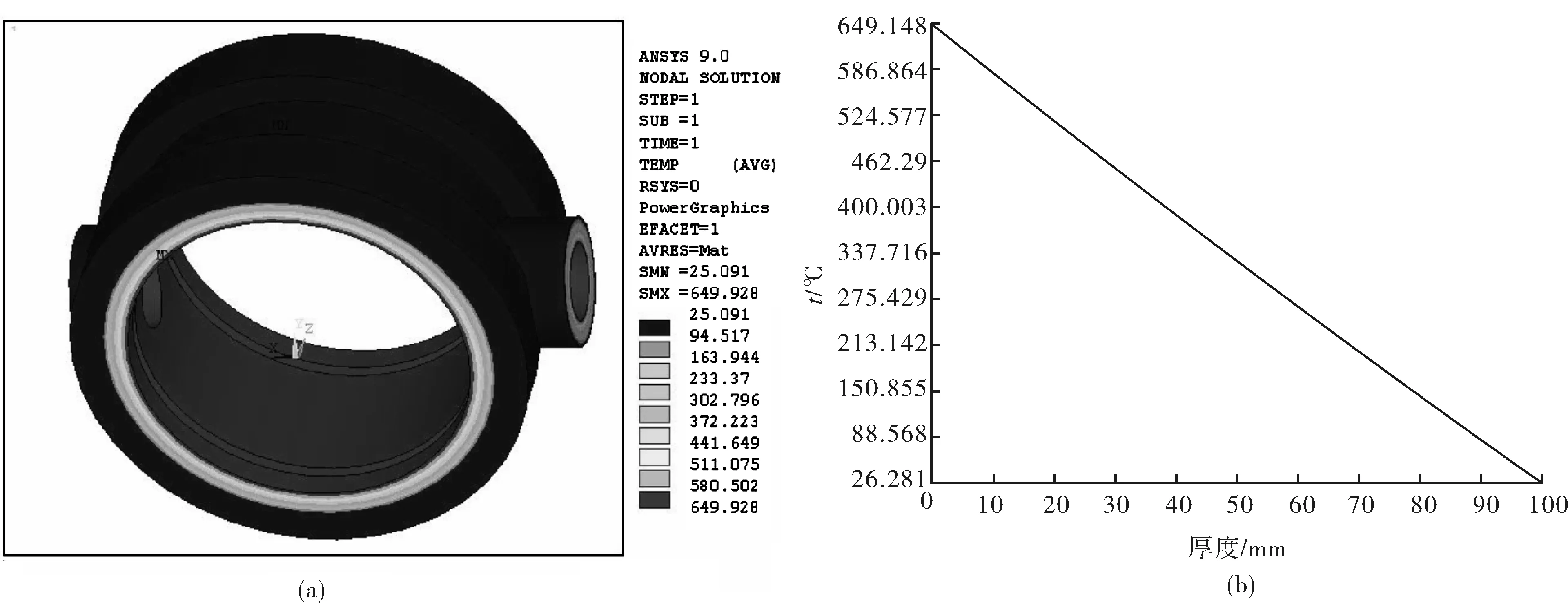
图10 保温层温度分布图Fig.10 The temperature distribution of insulation layer

4 蝶阀热应力分析

4.1 分析方法

ANSYS提供了三种热应力分析的方法[7]，分别为直接分析法、间接耦合法和直接耦合法.

上述热分析中采用SOLID70单元进行热分析，这里根据间接法进行热应力分析，采用ETCHG命令可将SOLID70单元转换成对应的SOLID45单元，并设置结构分析中的材料属性(包括热膨胀系数)以及前处理细节，如节点耦合、约束方程等，在读入热分析中的节点温度即可进行热应力求解.

4.2 材料属性及边界条件

根据蝶阀的操作条件，本文的初始条件及边界条件如下：

(1)材料属性

蝶阀的材质为304不锈钢，其弹性模量为1.95×105 MPa，泊松比为0.3，热膨胀系数为1.7×10-5℃.蝶阀保温层的材料为防水泡沫石棉，其刚度远小于304不锈钢，可不考虑保温层对热应力的影响.

(2)温度载荷

蝶阀的初始操作温度为650 ℃，保温层外表面与空气自然对流换热.稳态条件下，温度数据通过热分析计算得出，并保存在*.rth文件中，进行热分析时，通过GUI：Solution>Load Apply>Temperature>From Thermal Analysis命令，输入或选择热分析结果文件名*.rth，可将稳态热分析所得温度场加载到热应力分析模型.

(3)边界条件

在整体分析模型入口端的断面上施加固定边界，而另一端的断面保持为平面，即耦合轴向方向的位移.

4.3 计算结果

图11显示了蝶阀阀座不同方向上的位移，其中图11(a)为径向位移，结果表明阀座筒体径向位移均匀，阀座筒体内壁径向位移为6.6 mm左右；图11(b)为周向位移，结果表明蝶阀阀座的周向位移很小，可以忽略不计，这是因为阀座温度沿周向分布均匀；图11(c)为轴向位移，结果表明其轴向位移较大，最大值为16.72 mm.值得注意的是，蝶阀的轴向位移不仅与温度有关，还与其轴向边界条件有关.

图11 蝶阀阀座的位移Fig.11 The displacement of the valve seat

图12显示了蝶阀阀座的各种应力，其中12(a)为径向应力，12(b)为周向应力，12(c)为轴向应力，12(d)为等效应力.结果表明蝶阀阀座的各应力值较小，最大径向应力值为13.6 MPa，最大周向应力值为28.9 MPa，最大轴向应力值为15.2 MPa，最大等效应力值为27.7 MPa.值得注意的是，本文分析中将入口一侧取为固定支撑，而另一端自由支撑[8]，这样处理并不是实际工况，仅为平衡阀座的各向应力，而根据圣维南原理，该固定边界仅影响固定支撑附近的应力状态，而不影响远端的应力状态.因此，阀座出口端附近均匀的应力分布状态是真实的.

图12 蝶阀阀座的各种应力Fig.12 The stresses of butterfly valve seat

5 结 语

针对高温蝶阀在运行过程中存在热变形的问题，对阀座及其保温层的温度分布和应力状态进行了分析，结论如下：

(1)阀座保温层为100 mm时，阀座筒体整体上温度均匀，且沿壁厚温差仅为1 ℃左右；阀座圈处温度沿厚度的温差较大，最大温差约为10 ℃；阀座圈处的筒体沿壁厚的温差约为2 ℃；而保温层的温度沿厚度呈线性递减，不仅阀座筒体温差非常小，且保温层外表面温度较低，结果表明保温层选取100 mm是合适的.

(2)蝶阀在650 ℃操作条件下，阀座筒体径向位移均匀，内壁位移值为6.3 mm左右；周向位移很小，可以忽略不计；轴向位移较大，最大值为16.72 mm.

(3)，当保温层为100 mm时，产生的热应力很小，阀座筒体的所承受的等效应力较小，最大值仅为27.7 MPa，满足安全使用要求.

致 谢

在此特别感谢国家自然科学基金项目(50976080)以及武汉工程大学科学研究基金项目(14125061)给予的大力资助.

参考文献:

[1] 张为人. 阀门[M].上海:上海翻译出版社,1987.

Zhang Weiren. Valve[M].Shanghai: Shanghai Translation Publishing House,1987.(in Chinese)

[2] 吕荣美. 高温阀门的高温等级和主体材料[J]. 通用机械,2008(7):63-65.

LV Rong-mei. The Main Material and High grade of High-temperature Valve[J]. General Machinery, 2008(7):63-65.(in Chinese)

[3] 何培堂,刘先东,张志军,等. 高温阀门设计中的关键技术[J]. 炼油与化工,2002,13(4):27-29.

HE Pei-tang,LIU Xian-dong,ZHANG Zhi-jun,et al.Key Techniques in the Design of High-temperature Valve[J]. Refining and Chemicals, 2002,13(4):27-29.(in Chinese)

[4] 张洪信,赵清海. ANSYS有限元分析完全自学手册[M].北京：机械工业出版社,2008.

ZHANG Hong-xin, ZHAO Qing-hai. Complete Self-study Manual of The ANSYS Finite Element Analysis[M].Beijing：China Machine Press,2008.(in Chinese)

[5] 李标栋,施迪华. 泡沫石棉—安全、高效的绝热隔音材料[J]. 能源工程,1988,0(1):42-43.

LI Biao-dong,SHI Di-hua.Foam asbestos—The security and efficient insulating material[J].Energy Engineering, 1988,8(1):42-43.(in Chinese)

[6] 姚山,陈宝庆,戴利欣，等. 基于激光快速加热的金属材料热扩散率及导热系数快速测量方法的研究[J].热科学与技术. 2005,4(1):87-90.

YAO Shan,CHEN Bao-qing,DAI Li-xin,et al.Study on rapid measure of metallic material heat conductivity based on laser rapid heating[J]. Journal of Thermal Science and Technology. 2005,4(1):87-90.(in Chinese)

[7] 孔祥谦. 热应力有限单元法分析[M].上海：上海交通大学出版社,1999.

KONG Xiang-qian.The Thermal Stress Analysis by Finite Element Method[M].Shanghai:Shanghai Jiao Tong University Press,1999.(in Chinese)

[8] 丁克勤，刘关四，魏化中，等.快开式压力容器型型密封圈有限元公析[J].武汉工程大学学报，2013，35(8)：53-56.

DING Ke-qin,LIU Guan-si,WEI Hua-ahong,et al.Finite element analysis of special-shaped sealing ring on quick actuating pressure vessel[J].Journal of Wuhan Institute of technology,2013,35(8):53-56.(in Chinese)