距离与多普勒二维长时间相参积累方法

刘俊豪， 陈 潜， 陆满君

（上海无线电设备研究所，上海200090）

0 引言

随着隐身技术和高性能武器装备的发展，飞机、导弹等目标的雷达散射截面积（RCS）降低了一到两个数量级，使现有雷达系统的探测距离范围减小，检测性能大为降低，在现代雷达中常采用增加积累时间的方法提高隐身等微弱目标的检测性能［1-3］。而在长时间相参积累过程中，由于雷达与目标之间相对距离、相对速度变化引起的距离走动、多普勒扩散现象，严重影响目标能量的积累和检测。

因此，研究有效的校正距离走动和多普勒扩散补偿方法是改善现代雷达检测性能的重要途径之一［1］。

长时间相参技术中，对距离校正和多普勒补偿的方法很多。其中，Keystone变换的方法能在未知速度的情况下进行距离走动盲补偿，文献［3～5］对Keystone变换的原理和快速算法进行阐述，其可以对一定速度范围内的跨距离单元进行统一补偿，但是未考虑多普勒扩散问题。对多普勒扩散的补偿，文献［6～8］分别采用Hough-Wigner变换、分数阶傅里叶变换、短时傅里叶变换等时频分析的方法，由于时频分析过程中双线性变换运算量大，本文采用文献［1］提出的Dechirp方法。

本文将Keystone变换和Dechirp方法结合，解决距离和多普勒二维走动问题，并采用Chirp-Z变换快速实现Keystone变换减小运算量，最后通过仿真分析验证算法的有效性和检测性能。

1 信号模型

假设雷达发射LFM 信号，对于匀加速运动单点目标回波信号一个相参积累间隔（CPI）内雷达接收到的第m 个回波基带信号为

式中：t和tm分别为快时间和慢时间（tm＝mT，其中T 为脉冲重复间隔（PRI））；fc为载波频率；c为光速；Ar为点目标的回波幅度；R（tm）＝R0+vtm+0.5atm2，其 中a 为 目 标 径 向 加 速 度；R0和R（tm）分别为t0和tm时刻目标相对于雷达的径向距离；p（t）＝rect（t／Tp）exp（jπγt2）为发射的LFM信号。

式（1）的频域形式：

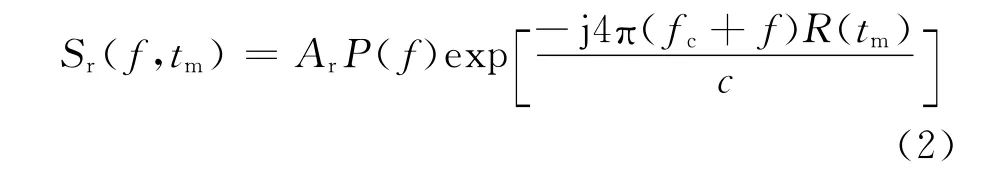
式中：P（f）为p（t）的频域。上式在距离频域乘以P＊（f）进行匹配压缩，得

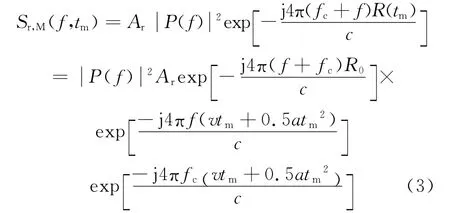
式中：第二个指数项中v和a 引起距离走动；第三个指数项中a引起多普勒扩散。

式（3）的时域形式为

基带回波通过脉冲压缩后其包络为离散sinc函数，其中心频率在2R（tm）／c处。

因此，目标的速度和加速度会造成每个回波脉冲压缩之后包络中心都不同，从而引起跨距离走动。而加速度对多普勒相位的影响，相当于产生一个线性调频信号，从而产生多普勒扩散现象。

2 距离和多普勒二维补偿算法原理

2.1 Keystone变换对距离走动补偿

式（3）中多普勒频率随慢时间变化，为了消除这种变化，定义虚拟时间τm，其与慢时间的关系为

式中：β为Keystone变换系数。

变换之后在f-τm平面，原来的信号采样点随慢时间呈梯形格式（或Keystone形格式），因此称为Keystone变换。

对式（3），在快时间频域信号作变量代换，即完成Keystone变换。变换后为

式中：A1＝Arexp（-j4πfcR0／c）。在式（6）相位项中，因为fc≫B，故fc／（f+fc）≈1。

Keystone变换后的时域形式：

式（7）可以知道，sinc函数代表的距离包络已经得到校正。为了便于数据处理，Keystone变换可以在f-τm平面通过插值将数据格式变成矩形。但是插值运算量大，下面通过离散化推导出在频域处理的快速算法过程。

设快时间t和慢时间tm的离散采样顺序分别为n和m，并设采样点总数分别为N 和M。

两个时间变换的频域分别为距离频率域（f）和多普勒域（fd），分别用l和k 表示，而两者的采样总数分别为L 和K，且有N＝L，M＝K。信号带宽为B，则f＝lB／L，tm＝mT。并令η＝B／（fcL），于是有

由于加速度对包络走动的影响较小，而Keystone变换主要完成包络的校正，对式（3）不考虑加速度，其离散形式为

式中：fdc＝-2vfc／c。将虚拟时间τm离散采样的顺序以m′表示，其采样总数为M；与虚拟时间τm相对应的虚拟离散多普勒采样点的顺序以k′表示，其总数为K′（＝K＝M）。

因此，将Sr，M（l，m）转换为Sr，M（l，m′），即完成Keystone变换。

可以通过傅里叶变换将Sr，M（l，m）变换到Sr，M（l，k′），然后通过逆傅里叶变换得到Sr，M（l，m′）。变换如下：

对于式（11）可以通过IFFT 实现，而对于式（10）指数项非均匀DFT 形式，傅里叶变换不能用FFT 实现。

对于该问题，采用线性调频Z 变换（CZT）的方法将DFT 转化成FFT 实现，可以大大降低运算量。

令a＝1+ηl，式（10）变换为

式中：W ＝exp（-jπa／M）；傅里叶变换对变量m进行运算。上式得到快时间频域和慢时间频域，将其快时间维做IFT 得到距离和多普勒维的相参积累结果Sr，M（n，k）。

在欠采样时，对多普勒模糊数的补偿只需在Keystone变换后，乘以补偿因子：

式中：F 为多普勒模糊数，fr为脉冲重复频率（PRF）。

在实际实现过程中需要对多普勒模糊数进行搜索，如果在末制导寻的雷达中，可以利用预装信息减少对模糊数的搜索，整个补偿过程如图1所示。

2.2 Dechirp对多普勒扩散的补偿

包络校正后如式（7），此时还受到加速度引起的多普勒相位调制的影响，需要对多普勒进行补偿，然后才能相参积累。

对多普勒走动补偿采用解线性调频（Dechrip）的方法。将式（7）乘以exp［j2π（a′／λ）］，当a’＝a时，二次相位得到补偿，从而使相位随时间均匀变化，然后通过FT 实现相参积累。a′可以按照下式进行估计

图1 Keystone变换快速实现流程图

在加速度范围内，以步进的方法对加速度进行搜索，对得到加速度对应的积累峰值，然后选大处理、恒虚警检测，确定目标是否存在，并给出目标的距离、速度、加速度信息。

3 仿真实验与分析

为了验证算法的有效性和检测性能，现对所采用的算法进行计算机仿真。

目标和雷达参数：设单点目标相对速度v＝2500m／s，加速度为500 m／s2相向雷达运动，加速度的最大搜索值为600m／s2；载频为10GHz，信号带宽B＝20 MHz，时宽Tp＝4μs，采样频率fs＝20 MHz，重频PRF＝25kHz，相参积累脉冲数N＝4096。

相参积累时间为163.8 ms，距离分辨率ΔR＝7.5m，跨距离单元数为54，跨多普勒单元为894。仿真过程中加入SNR＝-10dB的高斯白噪声，仿真过程的结果如下。

图2是对接收信号进行匹配压缩，在噪声中能够看出包络走动现象。直接对包络进行FFT操作，即动目标检测（MTD）的结果如图3、图4所示，其中图4是图3的俯视图。在相参积累时间内，直接MTD 使回波能量分散在多个距离和多普勒单元（图4），也正是这个原因使得积累幅度不高，检测性能较差。

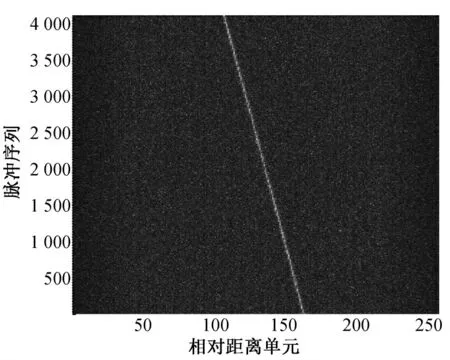
图2 匹配压缩包络轨迹

图3 MTD 结果

图4 MTD 结果俯视图

对包络做Keystone变换使包络对齐，结果如图5所示。

图5 Keystone变换后的包络

包络对齐之后，由于加速度的影响使多普勒相位不为线性，直接FFT 操作出现跨多普勒单元现象，如图6所示。

采用Dechirp方法对加速度进行搜索补偿，使多普勒相位线性变化，直接FFT 实现相参积累，结果如图7所示。

图6 包络校正后直接FFT 结果

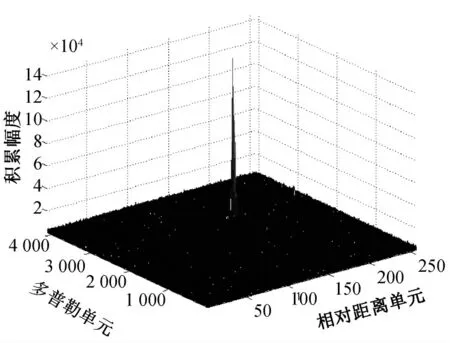
图7 距离和多普勒补偿后相参积累结果

从图中可以看出，通过本文的方法，积累幅度得到较大提高。

对不同输入SNR 进行1 000次Monte Carlo实验，实验结果如图8所示。仿真中MTD 的脉冲积累个数为不出现距离和多普勒走动的最大积累个数为75。

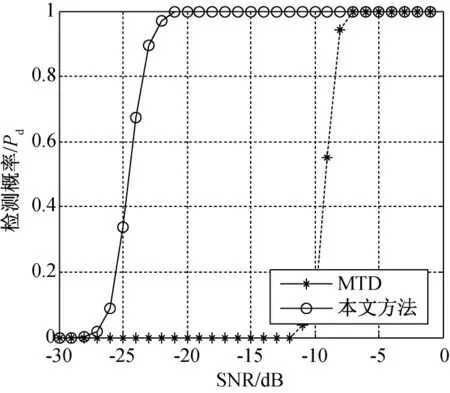
图8 虚警概率10-6时目标检测概率曲线

从图中可以看出，在虚警率为10-6，检测概率为0.8时，采用本文方法将目标的最小可检测SNR 比MTD 方法提高约15dB，检测性能显著提高。

4 结束语

本文针对长时间相参积累过程中出现的距离走动和多普勒扩散问题，提出结合Keystone变换和Dechirp方法进行距离走动校正和多普勒扩散进行补偿。最后通过仿真实验表明，本文方法能够显著提高积累增益和检测性能。

［1］ 保铮.雷达信号的长时间积累.第七届中国雷达学术年会论文集［C］.南京：中国电子学会，1999.

［2］ Carlson B D，Evans E D，Wilson S L.Search Radar Detection and Track with the Hough Transform，Part I：System Concept［J］.IEEE Transactions on Aerospace and Electronic Systems，1994，30（1）：102-108.

［3］ 张顺生，曾涛.基于keystone 变换的微弱目标检测［J］.电子学报，2005，33（6）：1675-1678.

［4］ 王娟，赵永波.一种改进的Keystone变换算法及其在微弱信号检测中的应用［J］.航空兵器，2011，（5）：3-6.

［5］ 赵永波，周晓佩.一种用于微弱信号检测的广义Keystone变换算法［J］.西安电子科技大学学报，2013，40（2）：120-125.

［6］ 刘建成，王雪松，刘忠，等.基于Wigner-Hough变换的LFM 信号检测性能分析［J］.电子学报，2007，36（6）：1212-1216.

［7］ 齐林，陶然，周思永，等.基于分数阶Fourier变换的多分量信号的检测和参数估计［J］.中国科学，2003，33（8）：749-759.

［8］ Xia X G.A Quantitative Analysis of SNR in the Short-time Fourier Transform Domain for Multi-Component Signals ［J］.IEEE Transactions on Signal Processing，1998，46（1）：200-203.