PWM 驱动系统中的对称功率滤波器设计

曹培培， 吴 晔

（上海无线电设备研究所，上海200090）

0 引言

PWM 功率驱动具有调速范围宽、快速性好和效率高的优点，在数字化伺服控制系统中得到了广泛应用。但是其开关噪声的频带宽、幅度大、辐射强，会对控制回路造成严重的干扰，破坏系统稳定性［1］。所以，消除开关噪声尤为重要。

PWM 功率驱动系统中的开关噪声问题得到了国内外学者的重视，美国Glenn研究院的学者提出了一种多级滤波器的设计方案［2］，APEX 公司也基于SA03 型功率放大器设计出了一种Power Design软件［3］，以上两种方案都是采用分割电感法的多级LCR 滤波器，虽然可以获得一定的抑制效果，但是其结构复杂，功耗偏大，同时也增加了设计难度。

本文以某高精度直接驱动式伺服跟踪平台为研究对象，针对PWM 功率驱动引起的噪声干扰问题，提出了一种新型的对称功率滤波器。根据滤波器的拓扑结构，建立其数学模型，并对其传递特性进行仿真分析。最后，通过实验验证了滤波器对噪声的抑制效果。

1 PWM 功率驱动系统中的噪声分析

直接驱动式伺服系统硬件结构如图1所示，包括了DSP电路、CAN 通信电路、PWM 功率驱动电路和A／D 采样电路。

测试结果表明，未加入滤波网络时，控制回路的地线存在与开关频率（30kHz）相近的高频噪声，影响了A／D 采样结果的精度。此外，电路中的基准电源同样受到辐射干扰，输出波形不稳定。基于以上问题，控制系统的稳定性和精度都无法得到保证。

经过分析，产生干扰的主要原因为：空间辐射和传导耦合。电机功率驱动电路在每次进行PWM 斩波调制时，会产生很大的开关噪声和电磁干扰，它不仅影响PWM 驱动电路，而且还会通过电源和地进入控制回路中，干扰路径如图1所示。

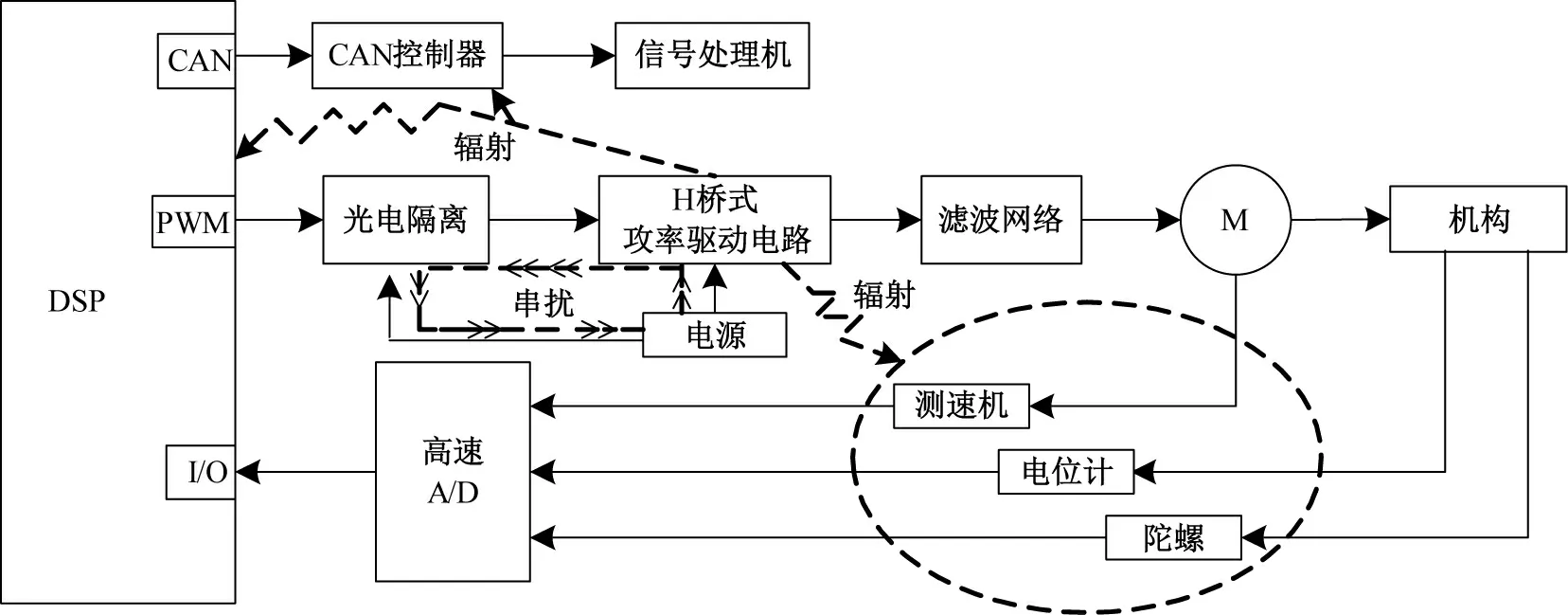
图1 控制系统硬件电路

抑制干扰的方法有很多种，例如电流平波、屏蔽、滤波和信号隔离等［1］。其中，电流平波需要在电机两端串接较大感值的电感，这种措施虽然可以抑制高次谐波，但会增加低频有用信号的衰减。此外，由于空间的限制，难以实现完全屏蔽和隔离。基于以上原因，选取滤波作为主要解决方案。

2 对称式功率滤波器设计

对称式功率滤波器不仅要保证足够的高频衰减，而且要有足够高的电流响应能力，以满足高精度动态伺服跟踪要求［4］。现有的一阶LCR 滤波器不能兼顾带宽和高频衰减要求，所以必须提高滤波阶次。

2.1 对称式滤波器的拓扑结构

PWM 功率驱动系统中，功率放大器输出到电机两端的是一对互补对称的方波，所以滤波网络的拓扑结构也必须对称。综合上述一阶LCR滤波器和多级分割电感式滤波器的优点，提出了一种新型的滤波器拓扑结构，如图2所示。

图2 对称式PWM 滤波网络拓扑结构

2.2 对称式功率滤波器频率特性分析

利用阻抗分析原理，将滤波网络分割成两个相同结构的电路，如图3所示。

图3 滤波网络分割图

令

得

由 图3 可 见，R ＝ （1／C1s + L3s +R1）／／（1／C4s）／／（Lms+Rm）。当U+＝0时，R 两端的电压为UO1、UO2，当U+＝0时，R 两端的电压则为UO3、UO4。

由于该滤波网络为对称结构，所以

再由式（1）、（2）和（3）得到滤波网络的传递函数为

研究对象中伺服电机的内阻Rm＝5Ω，电感Lm＝5mH，供电电压VM＝24V，PWM 载波频率f＝30kHz。设计要求纹波峰值应小于100mV，即频率在30kHz处的衰减应大于-48.9dB。根据滤波网络的传递特性，设计得到一组滤波参数为L1＝L2＝200μH，C1＝15μF，C2＝C3＝1μF，C4＝6.8μF，R1＝10Ω。将数值代入式（4），得到滤波器传递函数为

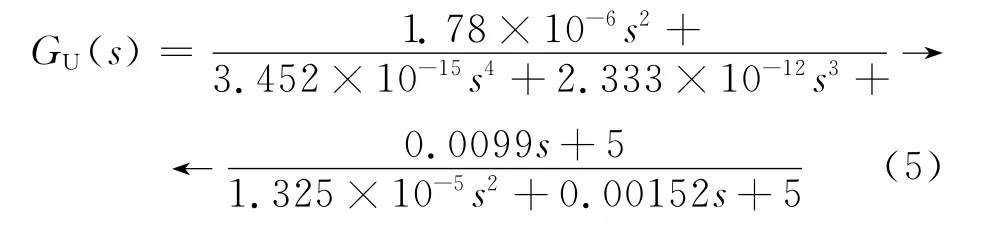
滤波器传递特性如图4所示，图中A 点坐标为（1.69kHz，-3dB），B 点坐标为（30kHz，-50.3dB），即滤波器的带宽为1.69kHz，在30 kHz处的衰减为-50.3dB，保证了足够的带宽和高频衰减量。图4中的传递特性曲线上存在谐振峰，它并不影响系统的稳定性，反而可以保证足够的闭环带宽。

图4 PWM 对称功率滤波器波特图

从滤波网络的拓扑结构和传递特性可以看出，L1、L2和C1值越大，带宽越小，高频衰减越大。C4与R1则主要用于调节系统的谐振和阻尼，其值越大，谐振越小。C2和C3的主要作用消除共模噪声，选取不当会引起较大共模分量。

2.3 滤波器对控制回路的影响

稳定跟踪平台控制回路采用双环路结构，如图5所示，内环由测速机构成速度反馈回路，完成对电机速度的控制，外环由电位计构成位置反馈完成对机构位置的控制［5］。

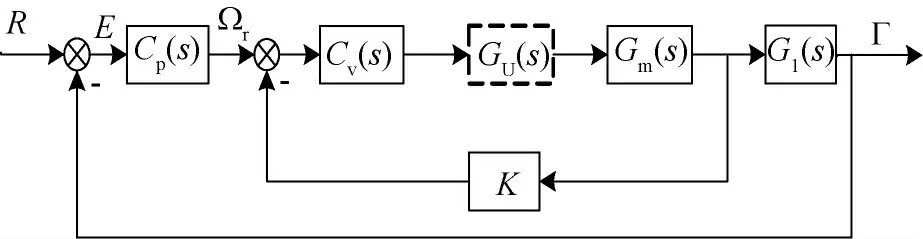
图5 控制回路模型框图

图5中，R 为控制角；E 为角误差；Ωr为参考角速度；U 为驱动电压；Ω 为电机角速度；Γ为天线指向角；Gm（s）为电机传递函数；Gl（s）为机构传递函数；K 为测速机反馈系数；Cv（s）为速度环控制律；Cp（s）为位置环控制律。

图6为滤波网路加入控制回路前后的波特图对比，从系统开环波特图中可以看出，未加入滤波网络之前系统的带宽为47.5 Hz，相角裕度为59.7°，加入滤波网络之后系统的带宽保持不变，谐振峰以及较大的相位滞后都出现在带宽以外，这说明滤波网络并不会改变系统传递特性。

图6 滤波前后控制回路的频域仿真

3 仿真和实验结果分析

3.1 Multisim 环境下时域仿真和实验结果对比

按照上述滤波器选定的器件参数，在Multisim 环境下建模，并进行时域仿真。由图7 可以看出，滤波器输出的峰峰值为±85mV，实测滤波器输出结果的峰峰值为±88.5mV。实测结果相比仿真结果存在±3.5 mV 的偏差。经过分析，产生偏差的主要原因为：滤波器元器件参数不一致，PCB布线也不完全对称。此外，在方波信号的上升沿和下降沿会产生30kHz毛刺，但是从实际滤波结果可以看出，该毛刺被抑制在±100mV以内，不会造成很强的辐射干扰。

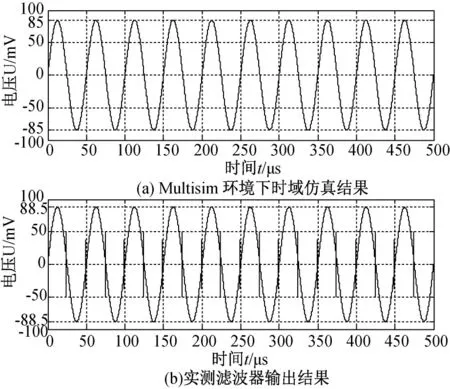
图7 滤波器输出的时域仿真结果和实测结果

3.2 滤波前后传感器信号采样对比

在控制回路未加入滤波网络时，陀螺电压和电位计电压采样结果毛刺很大。从图8可以看出，将滤波网络加入控制回路后，滤波器可以将陀螺电压和电位计电压的毛刺压制在±100mV 范围内，噪声辐射强度很弱，不会影响控制回路性能。

图8 滤波前后模拟信号电压采样结果

4 结论

本文分析了PWM 驱动系统中存在的开关噪声问题，比较了分割电感式和一阶LCR 功率滤波器的优缺点，提出了一种新型的对称式滤波器，并对滤波网络的传递特性进行了频域和时域仿真分析。实验结果表明，该滤波器将模拟信号的噪声幅度抑制在±100 mV 以内，将开关噪声的辐射干扰抑制在允许范围内。若滤波器中的元器件能够经过严格筛选，功放输出布线能够严格对称，滤波效果将会得到进一步改善。

［1］ 党永华.某PWM 驱动系统中干扰问题的分析［J］.火控雷达技术，2005，34：82-84.

［2］ Barbara H.Kenny，Walter Santiago.Filtering and Control of High Speed Motor Current in a Flywheel Energy Storage System ［C］.International Energy Conversion Engineering Conference，2004.

［3］ Barbara H.Kenny，Walter Santiago.Filtering and Control of High Speed Motor Current in a Flywheel Energy Storage System ［C］.International Energy Conversion Engineering Conference，2004.

［4］ 李海霞，韩丰田.高精度惯导平台低噪声PWM 功率驱动装置设计［J］.清华大学学报，2009，49（5）：668-672.

［5］ Apex Microtechnology Corp.Low Pass Filtering［Z］.2001.

［6］ 张艳，刘杨，陈峻山.导引头伺服系统控制回路Anti-Windup设计［J］.制导与引信，2011.32（3）：5-8.