多小波变换在导引头伺服机构信号降噪与缺陷识别中的应用研究
王家鑫, 周 郁, 袁 静, 周起华
(1.海军驻上海地区航天系统军事代表室,上海201109;2.上海无线电设备研究所,上海200090)
0 引言
导引头伺服机构是实现目标跟踪和视线轴稳定功能的执行机构,其结构复杂,技术难度大。导引头伺服机构的振动激励日益苛刻,服役环境日趋恶劣,这对伺服机构的动态性能提出了更高要求。伺服机构结构一旦出现缺陷或故障,将严重影响机构结构的运行品质,引发导引头动态参数恶化,甚至诱发系统失效,造成任务失败。在以往的导引头振动考核中,往往是通过伺服控制系统的性能指标来间接判断机构结构的好坏,因而难以判断导致系统振动考核欠佳的关键主导因素,更无法精确识别机构结构的潜在缺陷。
由于振动和噪声的普遍存在性、故障敏感性和易测量性等特点,使得振动噪声检测法已成为机械故障诊断的主要手段。然而导引头伺服机构结构复杂,部件繁多,所采集到的动态信号是各部件振动的综合反映。小波变换具有良好的时频多分辨特性[1],为伺服机构振动信号特征提取和结构缺陷识别提供了有力工具。近年来兴起的多小波变换是小波理论的新发展。由于多小波具有多个尺度函数和小波函数,克服了单小波无法同时满足的紧支性、对称性、正交性及高阶消失矩的优良性质,同时拥有多个时频特征有所差异的基函数,可以从不同角度匹配信号中不同的特征信息[2],使得多小波变换在伺服机构信号降噪与潜在缺陷识别等方面具有显著优势。
本文在介绍多小波基础理论的基础上,将多小波变换应用于导引头伺服机构的信号降噪与潜在缺陷识别。为有效评估某伺服机构的运行状态并识别其存在的潜在缺陷,对某导引头伺服机构进行振动噪声试验,采用性质优越的SA4多小波对振动信号进行滤波和降噪[3],并结合提纯轴向轨迹有效识别了伺服机构俯仰通道的结构对中不良缺陷。试验分析结果显示了多小波变换在信号降噪与结构潜在缺陷识别中的可行性和优越性。
1 多小波基础知识
1.1 多小波定义及其性质
所谓多小波是指由两个或以上的函数作为尺度函数生成的小波[4]。设Φ(t)=[φ1(t),φ2(t),…,φr(t)]为r 重 尺 度 函 数,且 满 足 两 尺 度 矩 阵方程:

式中:{Hk}和{Gk}为r×r的两尺度矩阵序列,也即是低通滤波器和高通滤波器系数;Ψ(t)为与Φ(t)对应的多小波函数。
常用的多小波包括GHM 多小波[5]、Chui-Lian多小波[6]、Hermite样条多小波[7]、SA4多小波等[3]。其中,SA4多小波具有紧支性、正交性、对称性和较高阶逼近阶,可避免因数据截断和信号重构所产生的误差,保证信号无冗余、无疏漏分解,且更好地逼近函数。SA4的两尺度矩阵方程如式(3)和(4),多尺度函数和多小波函数如图1所示。

其中:

其中:

图1 SA4多小波


1.2 离散多小波变换
在正交多分辨分析情况下,根据两尺度矩阵方程(1)和(2)可得到多小波的分解式为

同理,可得到多小波重构算法为

式中:符号* 表示共轭转置;cj,k为二维低频分量;dj,k为二维高频分量。
1.3 多小波前处理
多小波分解和重构是多输入多输出系统。需要对数据进行前处理,把一维的输入信号变为矢量输入。相应后处理为前处理的逆过程。在数据降噪中,重复采样的前处理方式效果相对较好[8],因此在本文后续应用中采用该方式。设输入信号为fk,则重复采样的前处理具体表达式为

2 多小波变换在导引头伺服机构缺陷识别中的应用研究
2.1 导引头伺服机构结构
齿弧式伺服机构结构形式简洁、占用空间尺寸小、机械结构刚度高,具有偏航和俯仰两个正交轴系的天线支撑平台。在俯仰通道中,陀螺稳定装置与天线安装在俯仰框上,通过多级齿轮传动实现内置平台相对齿弧的回转运动;偏航通道同样采用多级齿轮传递方式,末级的齿弧构成内置俯仰通道的安装平台。伺服机构的简化模型如图2所示,图中显示了齿弧式伺服机构的偏航通道、齿弧和俯仰框等简化组成。
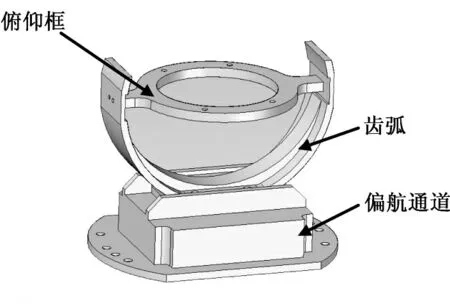
图2 伺服机构简化模型
2.2 振动噪声试验
基于机械故障机理,采用振动噪声检测方法可以有效诊断出伺服机构转轴、齿轮、轴承等机械关键零部件的不平衡、不对中、弯曲、油膜涡动、动静碰摩、磨损、裂纹、腐蚀、剥落、胶合、擦伤、断齿等故障,从而准确识别被测伺服机构的运行状态。因此,为了有效评估某导引头伺服机构的运行状态并识别其存在的潜在缺陷,搭建振动噪声试验台进行测试。试验设备包括被测伺服机构、传感器与调试器、数据采集仪器、数据存储与显示设备以及伺服机构控制设备等,如图3所示。其中,俯仰通道上的测点1#和2#分别布置在俯仰框传动链末级,且两者相互垂直并同步采样。
为了获得俯仰和方位通道匀速运动工况,在预定回路状态下对伺服控制系统输入三角波信号,转角变换范围为-20°~+20°,分别驱动伺服机构内置俯仰平台和齿弧的位置实现三角波变化。同时,试验中三角波信号的主频率分别设置为0.1 Hz、0.2Hz、0.3 Hz 和0.4 Hz,采 样 频 率 设 置 为1 250Hz。
2.3 试验分析

图3 伺服机构的振动噪声试验台
对俯仰通道0.4Hz转速下的振动信号进行分析。测点1#和2#的振动信号及其频谱如图4和图5所示。从图4可以看到,测点1#的振动信号表现为类正弦信号,主特征频率是转频0.3 918Hz及其奇数倍频1.208 Hz等。从图5可以看到,测点2#的振动信号表现为叠加毛刺的冲击与类正弦的混合信号。在时域信号的局部放大图中清晰可见强弱间隔的两类周期性冲击信号S1和S2(如图5所示),两类冲击间隔均约为2.4 990s,对应于俯仰通道运动到两侧换向时所产生的冲击。在图5 的频谱中转频及其各倍频非常明显,特别是偶数倍频0.7 998Hz及其倍频较为突出。基于机械故障机理学[9],从以上被测振动信号的时域和频域分析,并未发现伺服机构任何运行异常。

图4 测点1#的振动信号及其频谱
轴心轨迹是采用相互垂直的传感器同时采样得到的振动信号合成二维图[9]。轴心轨迹的形状和动态特性包含丰富的故障征兆,不同类型的故障对应有不同形状的轴心轨迹。采用图4和图5的振动信号合成原始轴心轨迹,如图6所示。可见,原始信号的轴心轨迹被大量噪声所污染,使得原始轴心轨迹复杂难以识别和处理。

图5 测点2#的振动信号及其频谱

图6 振动信号的原始轴心轨迹图

图7 多小波分析结果

图8 多小波分析后的提纯轴心轨迹图
下面采用多小波对图4 和图5 的振动信号进行滤波和降噪处理。采用SA4多小波对振动信号进行8层分解,前处理采用重复采样方式,然后对分解得到的低频信号进行单支重构得到提纯的低频振动信号,结果如图7所示。从图中可以看到,SA4多小波对这两个振动信号进行了滤波和降噪,大部分背景噪声已经被滤除。采用以上降噪后的信号合成提纯轴心轨迹,如图8 所示。可见,轴心轨迹表现为一个明显的八字型,是典型的转轴对中不良故障[9],这说明该伺服机构的俯仰通道存在转轴对中不良的潜在缺陷。
2.4 分析结果讨论
对于伺服机构的俯仰通道而言,机构中没有联轴节相关部件,而为什么会出现明显的转轴对中不良故障呢?在对伺服机构俯仰通道的结构形式进行详细分析后发现,机构中的俯仰框(如图2所示)两端的转轴与相应齿弧的配合孔要求有较高的同轴度,而其中俯仰框组合可以近似看做一个刚性联轴节。因此,俯仰框组合存在明显不同轴,类似于转轴对中不良中的平行不对中、角度不对中或综合不对中现象。随后,对该伺服机构进行解体,对其中的俯仰框和齿弧采用千分表进行测量,发现该伺服机构俯仰框两端转轴以及齿弧两端面的配合孔都存在类似角度不对中的不同轴现象。齿弧配合孔的不同轴比俯仰框转轴的不同轴更严重。经分析,该套伺服机构曾经历了严酷的耐久振动试验。长久大量级的振动激励导致齿弧配合孔位置发生改变(即出现不同轴现象),从而引发俯仰框两端转轴的不同轴,造成俯仰通道出现对中不良故障,这与分析结果一致。
3 结束语
为了有效评估导引头伺服机构的运行状态,本文将多小波变换引入导引头伺服机构的信号降噪与潜在缺陷识别中。文章首先简要介绍多小波定义及其性质、离散多小波变换和多小波前处理等多小波基础知识。其次,采用振动噪声检测试验对某导引头伺服机构进行测试与分析。由于受到背景噪声的干扰,时域分析、频域分析与原始轴向轨迹分析等均难以准确评判伺服机构的运行状态。本文采用性质优越的SA4多小波对伺服机构振动信号进行滤波和降噪,并结合提纯轴心轨迹有效识别伺服机构俯仰通道的结构对中不良缺陷。试验分析结果显示多小波变换在信号降噪与结构潜在缺陷识别中的可行性和优越性,该方法有助于准确鉴别伺服机构中的薄弱环节和故障隐患。
[1] Peng ZK,Chu FL.Application of the Wavelet Transform in Machine Condition Monitoring and Fault Diagnostics:a Review with Bibliography[J].Mechanical Systems and Signal Processing,2004,18(2):199-221.
[2] 何正嘉,袁静,訾艳阳.机械故障诊断的内积变换原理与应用[M].北京:科学出版社,2012.
[3] L.Shen,H.H.Tan,J.Y.Tham.Symmetric-Antisymmetric Orthonormal Multiwavelets and Related Scalar Wavelets[J].Applied and Computational Harmonic Analysis,2000,(8):258-279.
[4] 程正兴,张玲玲.多小波分析与应用[J].工程数学学报,2001,18(1):99-107.
[5] Geronimo JS,Hardin DP,Massopust PR.Fractal Functions and Wavelet Expansions Based on Several Scaling Functions[J].Journal of Approximation Theory,1994,78(3):373-401.
[6] Chui CK,Lian J-a.A Study of Orthonormal Multi-Wavelets[J].Applied Numerical Mathematics,1996,20(3):273-298.
[7] Dahmen W,Han B,Jia RQ,et al.Biorthogonal Multiwavelets on the Interval:Cubic Hermite Splines[J].Constructive Approximation,2000,16(2):221-259.
[8] Strela V,Heller P N,Strang G,et al,The Application of Multiwavelet Filterbanks of Image Processiong [J].IEEE Trans.Signal Processing,1999,8(4):548-563.
[9] 屈梁生,何正嘉.机械故障诊断学[M].上海:上海科学技术出版社,1986.

