面向复杂轮廓回转体电铸的阳极优化设计方法

蔡维展,朱增伟,朱 荻

(南京航空航天大学机电学院,江苏南京210016)

复杂轮廓电铸生产中存在铸层均匀性差、各部分性能不均的问题。在电铸过程中,当阴极形状和溶液成分确定后,阳极的位置和形状主要决定了阴极表面的电流密度分布,并最终影响电铸件的厚度均匀性及其机械性能。因为金属沉积速度直接影响沉积厚度和晶粒的生长,金属沉积速度通常又与电流密度成线性关系,而电流密度对合金电铸中成分含量有直接作用,所以控制阴极表面电场分布的均匀性是保证电铸件厚度均匀性及其机械性能的关键[1-3]。

金属电沉积发展过程中,阴极表面电场分布及电场分布均匀性的改善方法是许多科研工作者长久以来一直研究的问题。较早的Carl、Shih等对一些简单模型阴极电流密度分布的理论计算和实验结果进行过分析对比[6-7];Amiel和Glenn曾尝试寻找一种阴极表面电流密度值的测量方法[8];为提高沉积金属层质量,Engelmaier、Mehdizadeh等研究了辅助电极对阴极电流密度分布的影响[9-10];Jayakrishnan在实验中发现阳极位置对镀层金属分布有重要影响[11]。近年来,杨大春等研究了组合阳极电铸技术,并进行了大量实验[5];随着计算机仿真技术的发展,为象形阳极的设计提供了有利条件,德国的Lander对镀厚铬中镀层厚度不均的问题提出采用软件仿真进行象形阳极设计[12];王昆、高虹等提出基于ANSYS软件的电铸阳极优化设计方法[13-14]。

在前人研究的基础上,针对回转体件的电铸,为设计更好的阳极,满足阴极电场分布高均匀性的要求,提出了一种基于ANSYS的新的阳极优化设计方法。针对阴极局部电场强度突变难以消除的问题,给出了一种特殊辅助电极及其对应参数的选择和优化方法;将阴极节点和阳极控制点按阴极曲线的法向对应,同时把阴极场强的分布与阳极控制点的移动量联系在了一起;最终使阴极电场分布的均匀性达到了一个新的高度。

1 阳极形状的优化设计方案

由于所铸零件为回转体,优化分析中可将其简化为二维模型。优化分析采用通用有限元分析软件ANSYS11.0,求解后可获得阴极曲线上各节点的场强矢量,其代表了电流密度的分布情况;并将阴极曲线上场强的最大值与最小值之比作为目标函数进行优化,以追求阴极电场分布的均匀性,最终获得优化阳极轮廓。

图1是阳极优化设计方案的流程图。其步骤如下:

(1)根据零件内侧截面曲线形状构建阴极轮廓,通过复制并径向平移阴极曲线获得初始阳极轮廓曲线和两极间间隙,建立电场分析初始模型。

(2)求解初始模型,提取阴极电场强度分布,并对其进行分析。

(3)确定是否需要添加辅助电极,若需要,则构建辅助电极参数模型并优化。

(4)采用阳极轮廓整体调整过程,得到最终阳极轮廓。

阳极轮廓整体调整过程如下:

(1)初始状态,以阴极轮廓相同的边界曲线作为阳极的初始轮廓,构建电场分析几何模型。

(2)求解后获得阴极曲线上的场强分布,提取各节点的场强数值和法向矢量。

(3)按阴极节点的法向矢量法向对应到阳极曲线上,得到阳极曲线的控制节点。

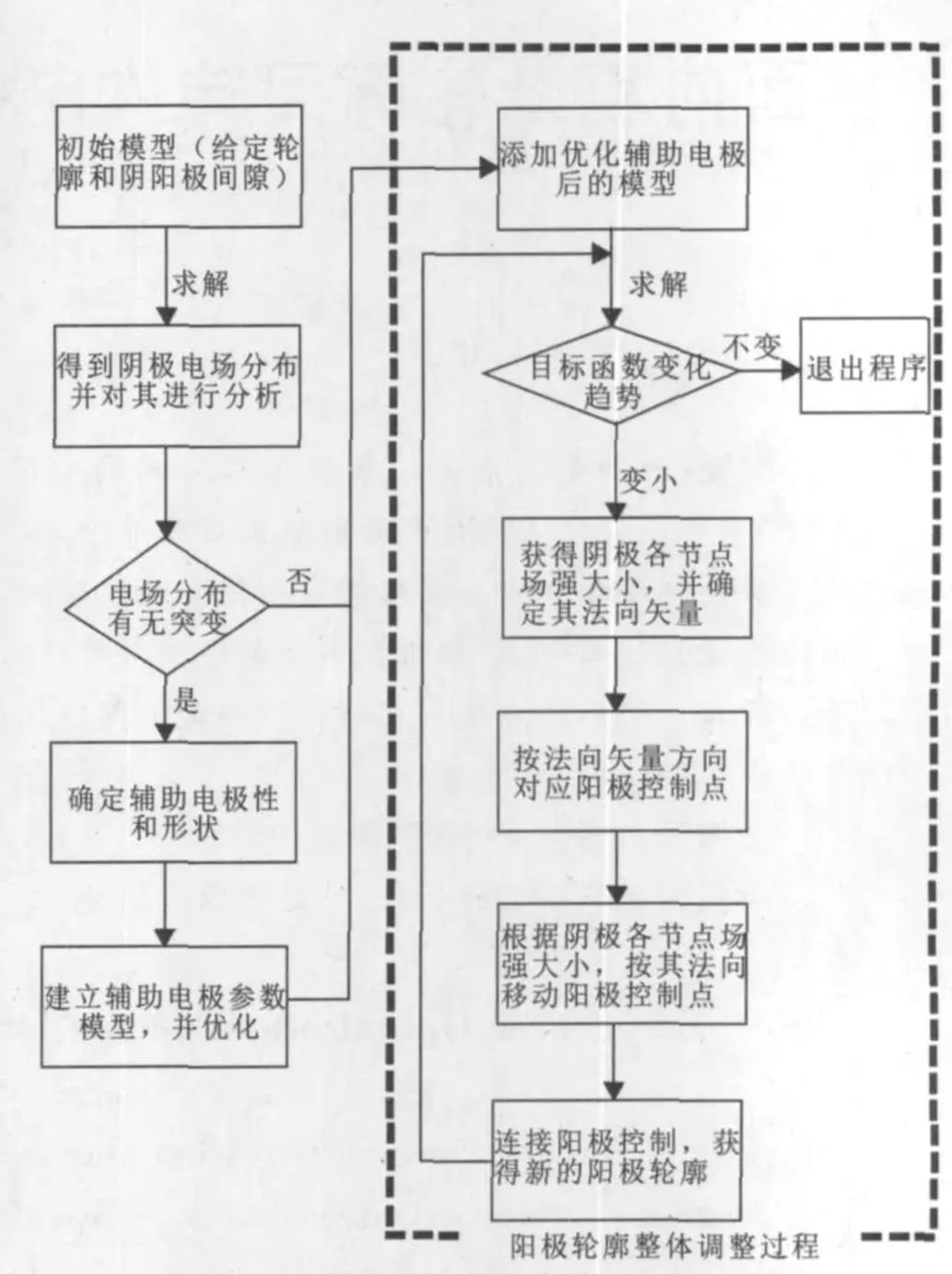
图1 阳极优化设计方案流程图

(4)根据阴极各节点的场强数值大小,相应调整阳极控制节点的距离,即阴极曲线上节点的场强越大,对应的阳极曲线上的控制点的移动距离越大;反之,阴极曲线上节点的场强越小,对应的阳极曲线上的控制点的移动距离越小。

(5)把移动后的阳极控制点连接成样条曲线,从而获得新的阳极轮廓,重新构建几何模型并求解。若目标函数减小,则进入下一次循环,反之退出程序。

2 阳极形状的优化设计方法

电铸初始模型通过复制并径向平移阴极曲线获得,求解后得到初始模型的阴极电场强度分布。以下对初始模型阴极电场强度分布变化较缓及存在局部突变的情况分别进行举例。

2.1 初始无场强突变的情况

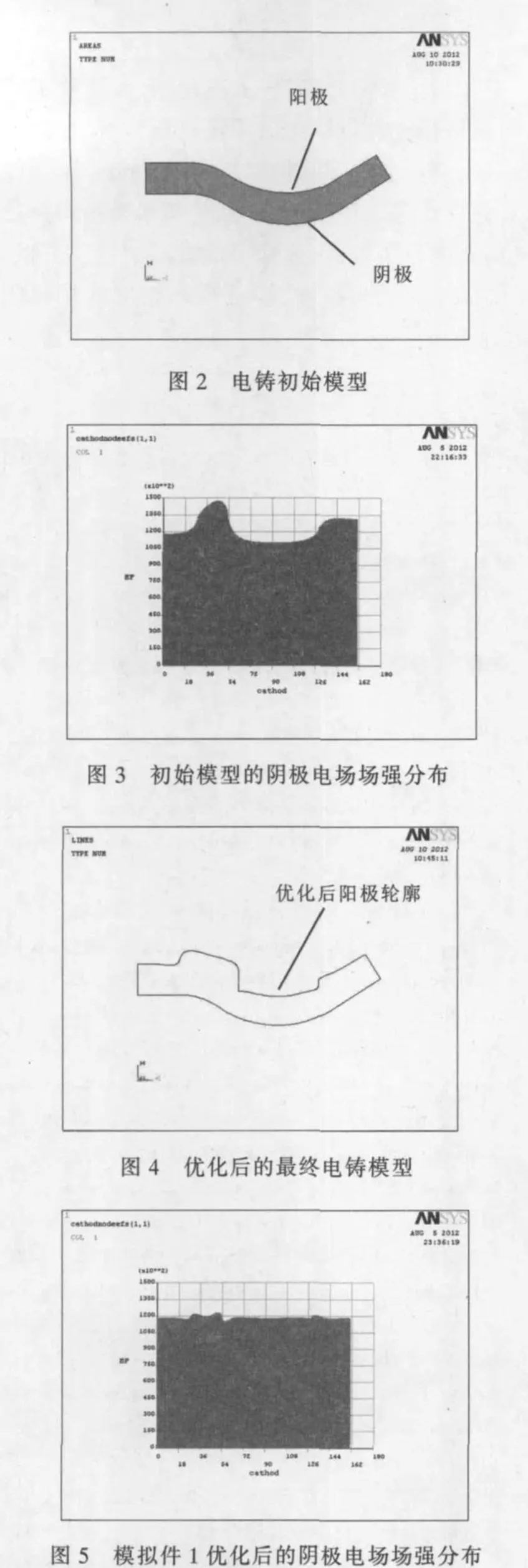
初始模型轮廓形状见图2,下侧轮廓线为阴极。图3是初始模型阴极表面电场强度分布,目标函数值为1.35。从图3可看出,其电场强度变化较缓,可直接采用整体调整法,优化后的轮廓和阴极电场强度分布见图4和图5。优化后目标函数由初始的1.35减小至1.06。

2.2 初始有场强突变的情况

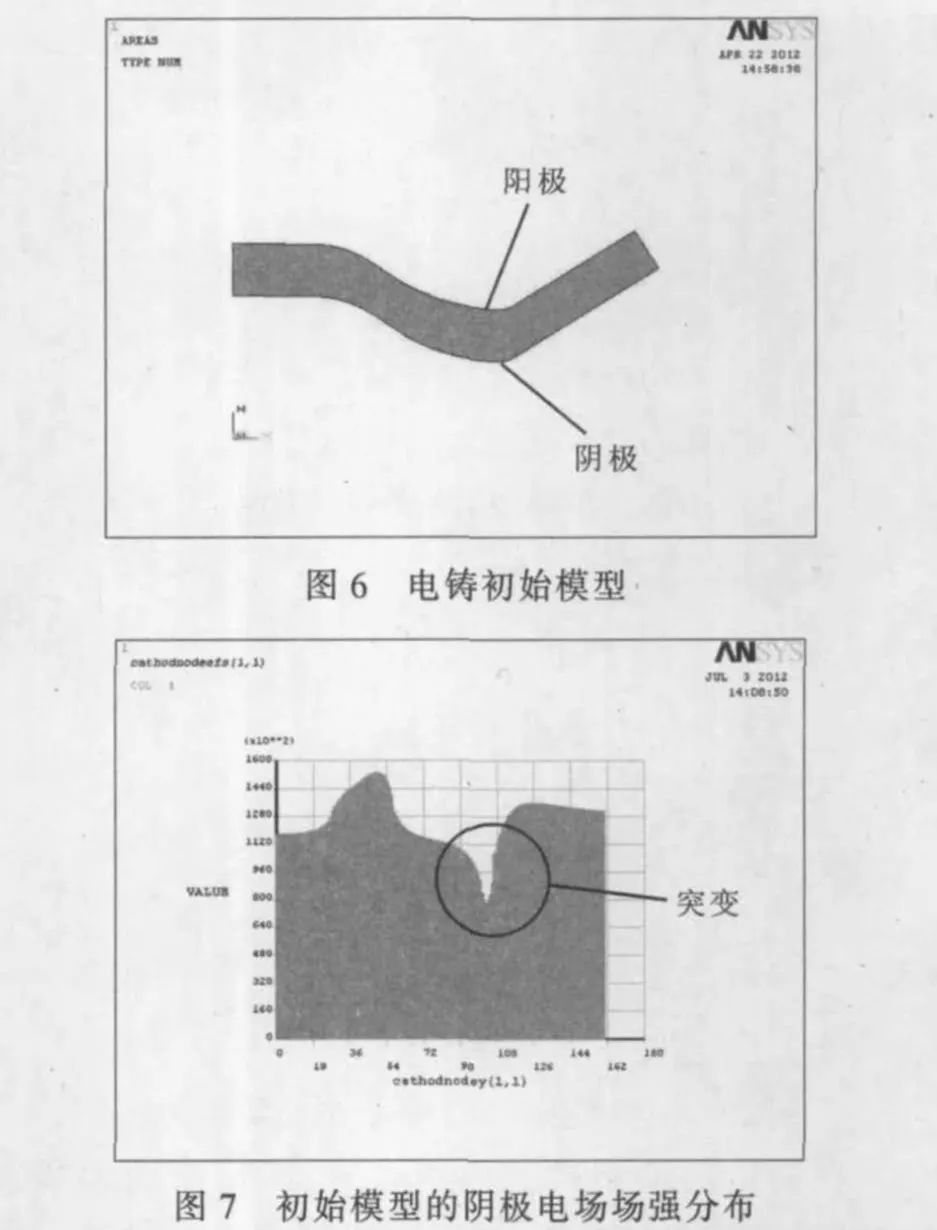
初始模型轮廓形状见图6,下侧轮廓线为阴极。图7是初始模型阴极表面电场强度分布,目标函数值为1.96。从图7可看出,局部小面积上存在下陷较深的电场强度突变。经分析发现,只依靠改变其对应的阳极段的形状和位置,难以完全填补该处电场的弱势。拟在此增加一辅助阳极,以减缓甚至消除该处小面积内的场强突变。

辅助电极的形状见图8,采用中间加电、两端绝缘的“凹”字状,以减小或避免其对阴极上除小圆弧段外其他部分的影响,达到较好的填补效果。为确定辅助阳极的尺寸和位置,设置了5个参数:参考点A(X、Y),中心导电段长度 L1,上端绝缘侧壁的长度L 2、下端绝缘侧壁的长度L3。编写程序,设定5个参数的变化范围和步长,将阴极填补区小圆弧段的电场场强的最大值与最小值之比作为目标函数值输出。

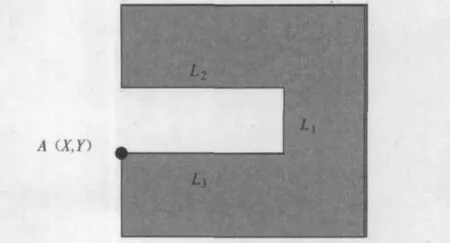
图8 辅助阳极模型

将目标函数最小的几个相近值对应的阴极电场强度分布图进行对比分析,确定最后结果,得到对应的参数。图9是加入辅助阳极后的模型,图10是其阴极表面电场强度分布,可看出,原来弱场强的突变区被填平了。

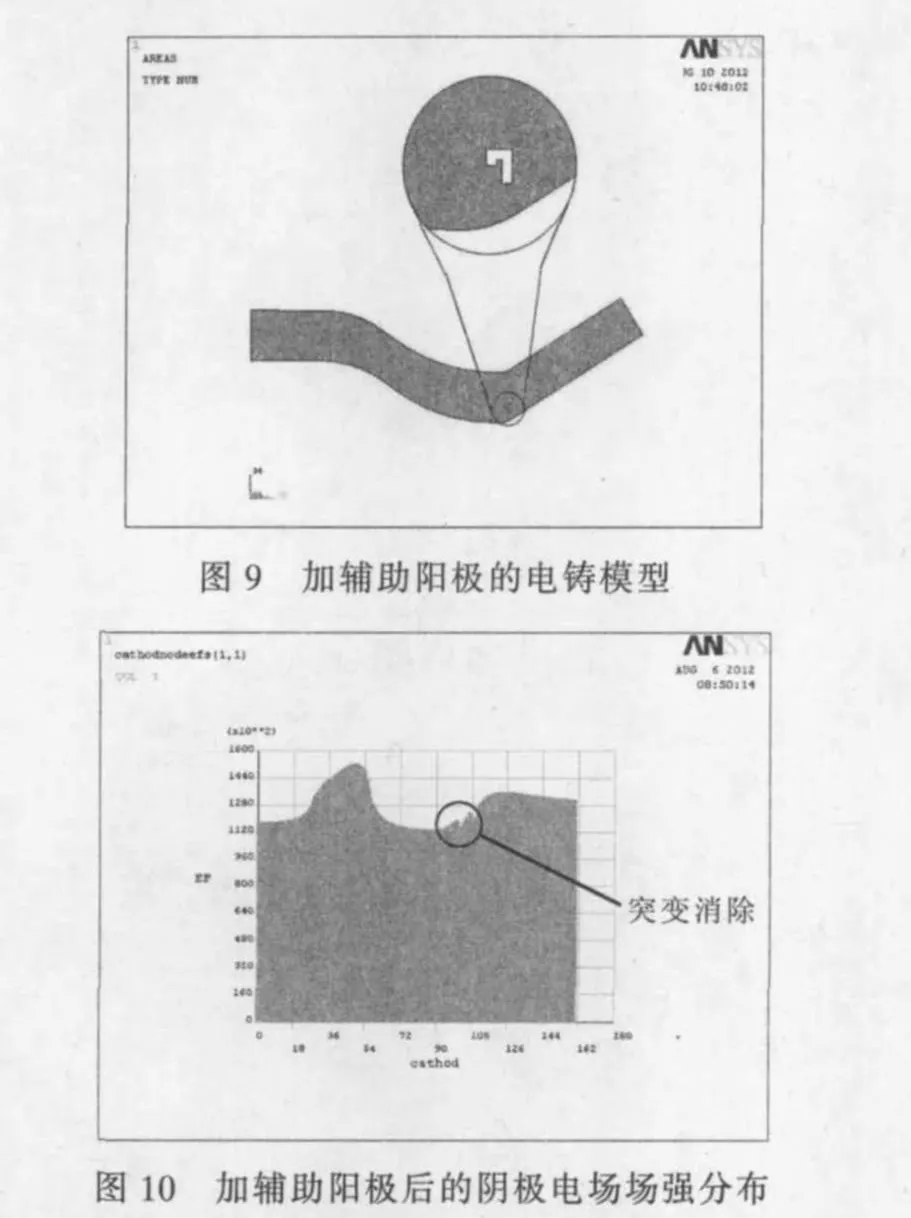
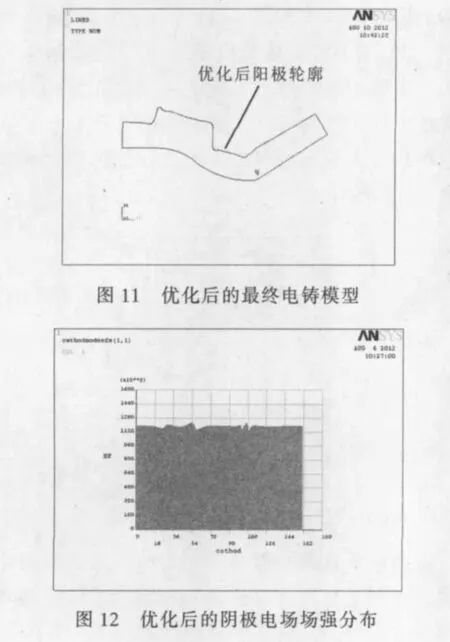
在确定辅助阳极的形状和位置后,采用编写好的阳极轮廓调整程序对初始阳极轮廓进行优化。优化后的轮廓和阴极电场强度分布见图11和图12。优化后的目标函数由初始的1.96减小至1.08。

3 结束语

本文利用有限元软件ANSYS的参数化编程手段,对回转体工件电铸中的阳极进行优化,实现了对阴极电场均匀性的控制。对于不同的回转体电铸件,需具体情况具体分析,根据其初始模型得到的阴极电场强度分布特点,选择添加或不加辅助电极,再调用阳极轮廓优化程序,即可得到相应的优化阳极轮廓。

[1] 陈钧武,何士桓.电铸原理与工艺[M].北京:化学工业出版社,2010.

[2] 杨建明,朱荻,王昆.电沉积技术中象形阳极的形状设计[J].机械设计与研究,2004(5):56-57.

[3] 曾华梁,吴仲达,陈钧武,等.电镀工艺手册[M].北京:机械工业出版社,2004.

[4] 龚曙光,谢桂兰,黄云清.ANSYS参数化编程与命令手册[M].北京:机械工业出版社,2009.

[5] 杨大春,云乃彰.组合式可溶性象形阳极电铸技术研究[J].热加工技术,2004(2):33-34.

[6] Carl W.Theoretical analysis of the current density distribution in electrolyte cells[J].Journal of the Electrochemical Society,1951(3):116-128.

[7] Shih H,Pickering H W.Three-dimensional modeling of the potential and current distributions in an electrolytic cell[J].Electrochemical Science and Technology,1987(3):551-558.

[8] Amiel F,Glenn G.A method for measuring local relative current density[J].Metal Finishing,1986(6):89-91.

[9] Engelmaier W,Kessler T,Alkire R.Current distribution leveling resulting from auxiliary bipolar electrodes[J].Journal of the Electrochemical Scciety,1978(2):209-216.

[10] Mehdizadeh S,Dukovic J,Andricacos P C.Optimization of electrodeposit uniformity by the use of auxiliary electrodes[J].Journal of the Electrochemical Society,1990(1):110-117.

[11] Jayakrishnan S,Dhayanand K,Krishnan R M.Metal distribution in electroplating of nickel and chromium[J].T ransactions of the Institute of Metal Finishing,1998(5):90-93.

[12] Lander H,Deconinck J,Nelissen G.Simulation as a tool for thickness control of chromium plating[J].Galvanotechnik,2008(9):2150-2157.

[13] 王昆,朱荻,杨建明.基于ANSYS分析的电铸阳极设计[J].航空精密制造技术,2004(6):17-19.

[14] 高虹,朱增伟,章勇,等.复杂型面电铸不溶性组合阳极优化设计[J].电加工与模具,2012(2):39-42.

[15] 周宁.ANSYS APDL高级工程应用实例分析与二次开发[M].北京:中国水利水电出版社,2007.

[16] 董久超,王磊,汤俊,等.电镀层均匀性的 Ansys模拟与优化[J].新技术新工艺,2008(11):114-117.