球面上两点间距离的求法

王功琪

(安顺学院数计系，贵州 安顺 561000)

《球面上的几何》是高中新课程的一个选修专题，本专题设置的目的是让学生了解除了平面几何外，还有多姿多彩的几何，而且各自都有自己的逻辑体系，球面几何就是其中的一种。球面几何在航海、航空、丈量土地、天文测量等方面有着非常重要的应用，这些问题都涉及到球面上两点间的距离，球面上两点之间的距离，实际上就是两点之间的大圆弧弧长。本文主要介绍球面上不同纬度、不同经度的两点间距离的三种求法。

1 异面直线法

要求球面上两点间的距离，根据弧长公式，应先求出这两点确定的大圆弧所对的圆心角，那么应该先求出这个圆心角所对的弦长，而要求得弦长，就把这两点作为异面直线上的两点从而用异面直线两点间的距离公式求得弦长，然后根据余弦定理求出圆心角从而求得两点间的距离。这种方法称为异面直线法。

例:A地位于北纬30°，东经60°，B地位于北纬60°，东经90°，求A，B两地之间的球面距离。［1］

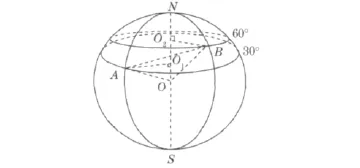
图1

解:如图1，设O为球心，R为球面半径，O1，O2分别为北纬30°圈和北纬60°圈的圆心，连结O1A，OA，O1B，OB，AB。

在直角△OAO1中，由A点位于北纬30°知∠OAO1=30°

所以O1O=OA sin∠OAO1=R AO1=OA cos∠OAO1= R cos30°=R。

在直角△OO2B中，∠OBO2=60°，

所以O2O=R sin60°=R，O2B=R cos60°=R。

因为O1A与O2B是异面直线，它们的公垂线为O1O2，这两条异面直线所成的角为γ=90°-60°=30°(经度差)于是，由异面直线上两点间的距离公式得:

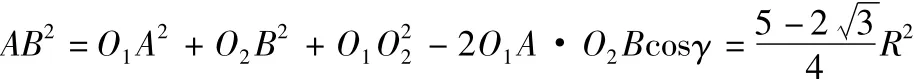
总结:这个方法的适用条件是已知两点处于不同经度和纬度，球面半径。若A，B两点分别位于纬度α1，α2，经度分别为β1，β2，球面半径为R，求A，B两点的球面距离的一般步骤是:

①如图1，先求O1A，OO1，O2B，OO2;②求O1O2(O1O2= OO2-OO1);③求A，B两点的经度差γ;

④根据异面直线两点间的距离公式求AB(AB2=O1A2= O1A2+O2B2+O1O22-2O1A·O2B cosγ);⑤求AB所对的圆心角∠AOB(cos∠AOB=);⑥求AB所对的大圆劣弧长。

2 球面三角法

当球面上两点确定的大圆弧是某个球面三角形的某一边时，这个球面三角形三条边和和三个对应角任意三个元素已知，我们就可以利用球面三角求出两点间的距离。这里的球面三角包含正弦定理、余弦定理等，这种方法叫做球面三角法。

球面三角形边的余弦定理是:对于任给半径为R的球面三角形△ABC，其三边a，b，c和三角∠A、∠B、∠C之间恒满足下述函数关系:

球面三角形边的正弦定理:对于任给单位球面上的球面三角形ABC，有

例:计算北京到重庆两地间的距离。

解:根据地理知识，北京位于北纬39°56'、东经116°20'，重庆位于北纬29°30'、东经106°30'的经纬度，而这两地与北极又刚好构成另一个球面三角形，在这个三角形中，北极到这两地的距离很容易求出，这两地的经度差也容易算出，于是在这个三角形中已知两边及其夹角，要求第三边，球面三角形边的余弦定理就可以解决。

假设地球半径为R=6400km。设N为北极点，B为北京，C为重庆，大圆弧BC的长度为所求。

在球面三角形NBC中，∠BNC=116.3°-106.5°=9.8°≈0.17弧度，

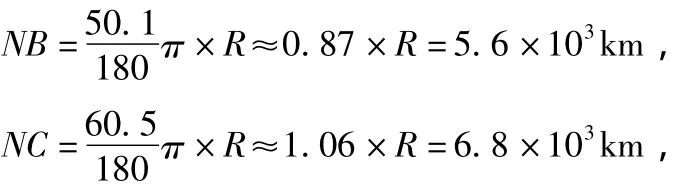
解球面三角形NBC，由球面三角形边的余弦定理:

即BC≈1.5×103km。

总结:应用这个方法的前提是容易找到两点确定的大圆弧所在的三角形，而且球面三角形的三个元素容易确定。例2中，我们很容易找到三角形NBC，且NB和NC的圆心角易求，从而可以求出他们的长度，而NB和NC的夹角∠BNC刚好是经度差，这些元素确定后，应用余弦定理解决是轻而易举的。

3 坐标法

当球面上给出两点的坐标，要求两点间的距离时，我们可以用球面距离的坐标公式求出两点间的距离，这种方法称为坐标法。

在半径为R的球面上，已知球面上两点A，B的坐标分别是A(x1，y1，z1)，B(x2，y2，z2)，则它们必满足方程x2+y2+z2= R2，则A，B两点的球面距离为:

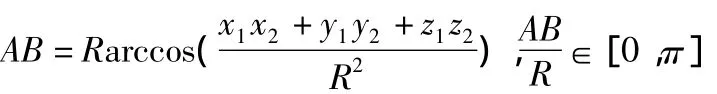
若点A，B用球面坐标表示为(R，φ，λ)，其中，∠AOB=φ，∠xOB=λ，由坐标变换公式，如图2:

图2

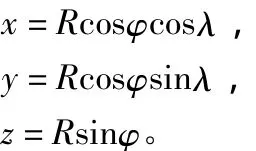
则 A (R cosφ1cosλ1，R cosφ1sinλ1，R sinφ1) 和 B (R cosφ2cosλ2，R cosφ2sinλ2，R sinφ2)两点间的距离为:AB= R arcos[ cos(φ1-φ2)-2cosφ1cosφ2sin2]。

例:计算上海(φ1=31.2°，λ1=121.5°)与乌鲁木齐(φ2= 44°，λ2=88°)之间的距离。这里的φ，λ分别表示点的纬度和经度，地球半径R=6370千米。

解:将两城市用A，B表示，则A，B间的距离是指他们的球面大圆弧长。由球面距离的坐标公式，得 AB=R arccos [cos(31.2°-44°)-2cos31.2°cos44°sin2]= R arccos0.8729=6370×0.6097≈3250(km)［2］

总结:这种方法适用条件是已知两点的坐标以及球面半径。

以上是不同纬度不同经度两点间距离的三种求法，每一种方法都有它适用条件，因此在选用求法时要注意方法的适用范围。而同一纬度或同一经度的两点间的距离则容易求得多。要求同一经度上的两点间的距离，只需计算纬度差作为两点确定的大圆弧所对的圆心角，然后应用弧长公式即可解决问题;而要求同一纬线上两点A，B的球面距离，过A，B作大圆，关键要求圆心角∠AOB的大小，而要求∠AOB往往首先要求弦AB的长，而要求弦AB的长，就应该先求出纬线圈中经度长和纬度差。

［1］孙庆阳.利用球面距离求地球表面距离的技巧［J］平顶山师专学报(自然科学版)1998年8月第13卷第4期

［2］项昭等.高中数学选修课程专题研究［M］贵阳.贵州人民出版社.2007年8月