裂纹间距对轮轨滚动接触疲劳作用下的钢轨表面多裂纹扩展趋势的影响

刘园

(上海海事大学 物流工程学院，上海 201306)

0 引 言

随着现代运输业的迅速发展，列车运行速度和载质量不断增加，由滚动接触而导致的钢轨表面裂纹已成为日益发展的高速铁路在安全方面的主要问题.实际上，由于轮轨接触而导致的钢轨裂纹是大量同时存在的，特别是钢轨表面斜裂纹，更是导致钢轨失效的主要缺陷形式之一.在对钢轨的巡视检查中发现，钢轨表面分布的斜裂纹多在钢轨踏面或是在转弯半径为400～2 000 m的钢轨外侧大量出现，并且可以在大范围内扩展.这种斜裂纹的间距大约为2～7 mm，沿与钢轨水平方向成15°～40°向钢轨深度方向扩展.[1-4]除这种特定形式的多裂纹缺陷以外，其他形式的疲劳缺陷，如表面剥离裂纹等，有可能同时存在于相邻的钢轨表面，虽然这种多裂纹缺陷的位置分布具有不确定性，但由于裂纹的萌生和扩展由该段钢轨线路上的载荷决定，裂纹的扩展往往也伴随着其他裂纹的萌生或扩展.当钢轨原有裂纹邻近位置萌生其他裂纹后，其所受载荷因为相邻裂纹的存在而重新分配，裂纹的扩展趋势也会发生一定的变化.这与新裂纹萌生的位置、裂纹尺寸、裂纹形状以及裂纹数量等因素都有很大的关系.[5-10]本文通过建立钢轨多裂纹的三维有限元模型，着重研究裂纹间距对轮轨滚动接触疲劳作用下的钢轨多裂纹扩展趋势的影响.

1 钢轨多裂纹有限元模型

建立轮轨滚动接触疲劳作用下的多裂纹有限元模型的思路见图1.假设两条裂纹均位于钢轨轨头表面，裂纹中心线与钢轨轴线重合.这里主要分析两条钢轨表面裂纹并存的情况，并可以就此进行一定的推广.令两钢轨表面裂纹半径分别为a1和a2，与钢轨表面所成倾角为α1和α2.在本文中假设两裂纹平行分布，故α1=α2=α.为便于与单裂纹条件下的裂纹扩展情况进行比较，多裂纹模型仍选用单裂纹模型的坐标系[11-12].图1中：t为裂纹间距；e为轮轨接触中心与原有裂纹的距离.

图1 轮轨滚动接触多裂纹模型建模思路

应用ABAQUS软件，根据UIC60轨道和S1002车轮的轮廓数据精确建立轮轨滚动接触的三维几何模型.裂纹的建模通过向ABAQUS模型中植入多个Zencrack裂纹块实现(见图2).裂纹块的三维网格划分及裂纹扩展方向的定义见图3.在裂尖前缘上共定义33个节点，各节点的初始裂纹扩展方向均定义为在原裂纹平面内，通过扩展角的计算判断裂纹的扩展方向是否发生改变.分析过程中综合考虑轮轨之间以及裂纹面之间的接触，通过定义不同的接触关系和摩擦因数，对两种不同形式的接触进行仿真.

图2 钢轨表面多裂纹三维有限元网格 图3 钢轨多裂纹块及裂纹扩展方向定义

2 裂纹间距对钢轨多裂纹扩展趋势影响

2.1 多裂纹有限元模型参数及计算结果

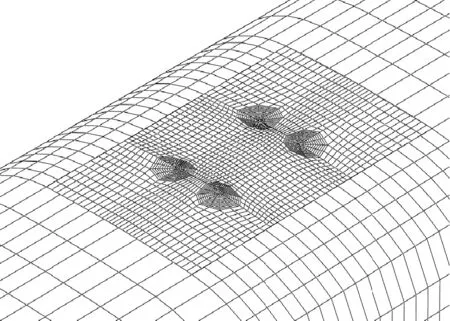
(a) t=20 mm

(b) t=10 mm

(c) t=5 mm

图4不同裂纹间距条件下的钢轨多裂纹模型网格划分

裂纹间距是影响钢轨多裂纹扩展的主要因素，随着裂纹间距的改变，相邻裂纹之间的作用程度会发生变化，轮轨滚动接触载荷在裂纹之间的分配也会发生变化.本文通过改变裂纹间距参数，分析等长多裂纹(a1=a2)在t分别为-20,-10,-5,5,10,20 mm时，在相同法向载荷条件下，裂纹深度方向尖端点C1和水平方向尖端点A1(B1)(见图1)的应力强度因子变化情况.t>0说明新裂纹位于原有裂纹后方，即车轮先经过原有裂纹，再经过新裂纹；t<0说明新裂纹位于原有裂纹前方，即车轮先经过新裂纹，再经过原有裂纹.t分别为5,10,20 mm时钢轨多裂纹的网格划分见图4.

在车轮法向载荷FN=100 000 N(法向接触载荷半径约为5 mm)，轮轨接触表面摩擦因数μ=0.1，裂纹面间摩擦因数μc=0.2，裂纹半径为5 mm，裂纹水平倾角为30°条件下，计算在不同裂纹间距时的裂纹尖端应力强度因子，结果见图5～8.

图5t>0时C1点应力强度因子

图6t<0时C1点应力强度因子

图7t>0时A1(B1)点应力强度因子

图8t<0时A1(B1)点应力强度因子

从图5和6可以看出，当原有裂纹附近出现新的裂纹后，原裂纹深度方向上的尖端点C1所受的载荷低于单裂纹情况，且随着裂纹间距减小，C1点所受载荷的幅度不断降低.当新裂纹出现在原有裂纹前方(即t<0，新裂纹位于原有裂纹左侧)时，应力强度因子曲线左侧幅值降低比较明显；当新裂纹出现在原有裂纹后方(即t>0，新裂纹位于原有裂纹右侧)时，应力强度因子曲线右侧幅值降低比较明显.

从图7和8可以看出，当原有裂纹附近出现新的裂纹后，钢轨表面的A1(B1)点所受载荷情况与单裂纹时的状况也有所不同.随着裂纹间距的减小，A1(B1)点所受载荷的幅度也不断降低.当新裂纹出现在原有裂纹前方(即t<0，新裂纹位于原有裂纹左侧)时，应力强度因子曲线左侧幅值降低比较明显，而KII曲线右侧幅值略有升高；当新裂纹出现在原有裂纹后方(即t>0，新裂纹位于原有裂纹右侧)时，应力强度因子曲线右侧幅值降低比较明显，且A1(B1)点所受I型载荷由拉伸载荷变为压缩载荷，而KII曲线左侧幅值略有升高.

2.2 裂纹间距对多裂纹扩展方向和扩展速率的影响

对每一车轮位置对应的钢轨裂纹尖端点的应力强度因子Kσ和Kτ进行求解，比较车轮经过钢轨一个载荷循环过程中的应力强度因子最大值Kσmax和Kτmax，从而对不同裂纹间距条件下钢轨裂纹是否发生扩展以及裂纹的扩展方向作出判断.[13-15]

应用有限元分析所得的钢轨裂纹尖端应力强度因子，可以对C1点和A1(B1)点的裂纹扩展状态进行判断，从而了解裂纹向钢轨深度方向和水平方向的扩展情况.[16]将a1=a2=5 mm，α=30°，μ=0.1，μc=0.2，FN=100 000 N条件下计算所得的C1点和A1(B1)点的裂纹扩展情况分别见表1和2.

表1 C1点裂纹扩展情况

从表1和2可以看出，对于裂纹深度方向上的尖端点C1，随着相邻裂纹间距的减小，裂纹扩展模式和扩展方向会发生变化.当t=20,10 mm时，C1点裂纹的扩展方向与原裂纹方向相同，扩展模式为II型.当t=5 mm时，当相邻裂纹出现在原有裂纹的前方(即车轮先经过新裂纹，再经过原有裂纹)时，裂纹的扩展模式发生改变，以I型模式发生扩展，且扩展方向向邻近裂纹的方向弯曲.从裂纹扩展速率看，邻近裂纹的出现会抑制原有裂纹的扩展，且扩展速率随着t的不断减小而不断降低.对于相同的裂纹间距，当相邻裂纹出现在原有裂纹前方时，裂纹扩展速率大于其出现在原有裂纹后方的扩展速率.

表2 A1(B1)点裂纹扩展情况

对于裂纹水平方向上的尖端点A1(B1)，随着相邻裂纹间距的减小，其扩展角度不断增加，裂纹扩展方向与相邻裂纹出现的方向相同.裂纹扩展速率的变化与C1点的变化趋势相同，即随着相邻裂纹间距的减小裂纹扩展速率不断降低，且对于相同间距的相邻裂纹，当其出现在原有裂纹的前方时，原裂纹的扩展速率比其出现在原有裂纹后方时大.

3 结束语

研究钢轨表面裂纹在其附近萌生等长度新裂纹的情况，发现新裂纹的出现会导致原有裂纹扩展速率降低.在裂纹深度方向上，裂纹扩展方向随着裂纹间距的减小而发生改变，当裂纹间距足够小时，裂纹的扩展模式由II型变为I型，且扩展方向向新裂纹弯曲.对于钢轨表面水平方向上的点，新裂纹的出现也会导致原有裂纹的扩展方向向新裂纹弯曲.由此可见，新裂纹的萌生虽然可以在一定程度上降低原有裂纹的扩展速率，但容易导致两裂纹融合，从而形成新的表面剥离裂纹或其他形式裂纹，而新裂纹的扩展速率可能会远远大于原有裂纹的扩展速率.因此，建议重视钢轨表面出现的多条间距较小的裂纹，并采取相应的措施以防止上述现象的发生，从而避免发生钢轨断裂事故.

参考文献：

[1] MUSTER H, SCHMEDDERS H, WICK K,etal. Rail rolling contact fatigue. The performance of naturally hard and head-hardened rails in track[J]. Wear, 1996(1/2), 191:54-64.

[2] LEWIS R, OLSSON U. Wheel-rail interface handbook[M]. UK: Woodhead Publishing Ltd and CRC Press LLC, 2009: 280-311.

[3] GROHMAN HD, SCHOECH W. Contact geometry and surface fatigue: minimizing the risk of headcheck formation[J]. Wear, 2002, 253(1/2): 54-59.

[4] TAKIKAWA M, IRIYA Y. Laboratory simulations with twin-disc machine on head check[J]. Wear, 2008, 265(9/10): 1300-1308.

[5] KAMAYA M. Growth evaluation of multiple interacting surface cracks, part I: experiments and simulation of coalesced crack[J]. Engineering Fracture Mechanics, 2008, 75(6): 1336-1349.

[6] KAMAYA M. Growth evaluation of multiple interacting surface cracks, part II: growth evaluation of parallel cracks[J]. Engineering Fracture Mechanics, 2008, 75(6): 1350-1366.

[7] KAMAYA M, KITAMURA T. Stress intensity factors of interacting parallel surface cracks[J]. Trans Jpn Society Mechanical Engineers, 2001, 68: 1112-1119.

[8] NODA N A , KOBAYASHI K, OOHASHI T. Variation of the stress intensity factor along the crack front of interacting semi-elliptical surface cracks[J]. Archive Applied Mechanics, 2001, 71(1): 43-52.

[9] HASEGAWA K, SHIRATORI M, MIYOSHI T,etal. Comparison of stress intensity factors of two flaws and a combined flaw due to combination rules[J]. ASME PVP, 2002, 39: 307-312.

[10] KAMAYA M, NISHIOKA T. Finite element alternating method for interacting surface cracks[J]. Solid State Phenom, 2007, 120(2): 147-153.

[11] 郑惠强, 刘园. 滚动接触疲劳作用下的钢轨裂纹萌生与扩展机理[J]. 上海海事大学学报, 2009, 30(2): 52-59.

[12] 刘园. 液体对轮轨滚动接触疲劳作用下的钢轨表面裂纹扩展机理的影响[J]. 上海海事大学学报, 2011, 32(1): 65-69.

[13] KANETA M, SUETSUGU M, MURAKAMI Y. Mechanism of surface crack growth in lubricated rolling/sliding spherical contact[J]. ASME J Applied Mechanics, 1986, 53(2): 354-360.

[14] OSUKA A, MORI K, MIYATA T. The condition of fatigue crack growth in mixed mode condition[J]. Engineering Fracture Mechanics, 1975, 7(3): 429-432.

[15] 朱从兵, 张卫国, 刘海洋. 岸边集装箱起重机箱型构件疲劳裂纹扩展分析[J]. 上海海事大学学报, 2008, 29(3): 74-78.

[16] SHNITZER T. Bruchmechanische analyse des wachstums von rollkontactermuedungsrissen in eisenbahnschienen[D]. Berlin: Berlin Technische Universitaet, 2007.