改进BPR路阻函数及其在EMME中的应用

周彪， 智路平， 李彬

(1. 上海海事大学 经济管理学院，上海 201306；2. 上海市交通港航发展研究中心，上海 200025)

0 引 言

路阻函数[1]用于描述车辆在道路上的行程费用(或时间)与道路交通条件之间的关系，能反映道路网络各组成部分的交通容量限制和拥挤效应，是交通量分配预测中的一项十分关键的技术，也是实施交通量分配的前提条件.

对路阻函数的研究已有许多成果，有许多不同形式的函数被提出并应用于实践中.如美国联邦公路局对大量路段进行交通调查后，通过回归分析得到BPR函数[2].DAVIDSON应用排队论基础提出有渐近性的路阻函数.[3-4]王树盛等[5]对路阻函数关系式进行推导及拟合分析.王元庆等[6]在“九五”交通科技重点攻关项目关于公路通行能力的研究中，重新标定BPR函数，建立模型.王炜等[7]针对中国国情提出路阻函数修正模型.霍飞[8]结合出行特征进行分析，确定与路阻函数相关的因素并对已有数学模型进行改进.还有基于Greenshields模型的包含速度、交通密度的路阻函数[9]以及在拥挤和非拥挤情况下基于Edie交通流模型的路阻函数[10].其中应用得比较广泛的是美国联邦公路局提出的BPR函数

1 改进路阻函数的导出

1.1 改进路阻函数应具备的性质

为保持与BPR函数模型的兼容,改进模型f*(va)应当具有性质(1)～(4)；为弥补BPR函数的内在不足，给改进模型增加性质(5)～(7).

(1)改进路阻函数f*(va)应当是一个严格递增的函数.这符合拥挤效应，也是配流结果具有唯一性的保证.

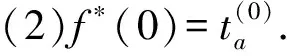
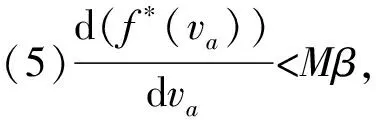
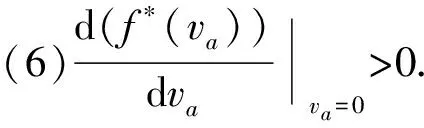
(7)改进路阻模型具有更短的计算机运行时间.

1.2 改进路阻函数的形式

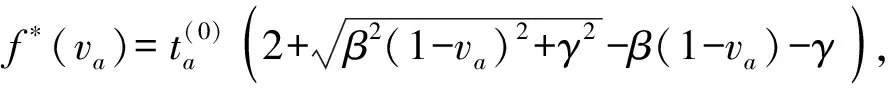
1.3 证明改进路阻函数的性质

下面依次证明本文的改进路阻函数具有第1.1节所列的7个性质.

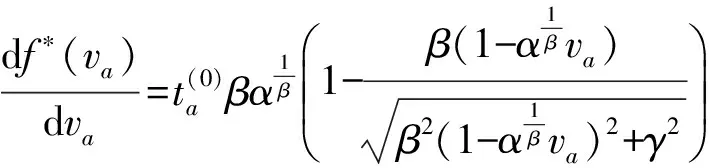
(4)函数凸性证明.易知

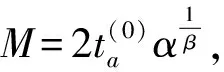
(7)关于模型在计算机内的运算时间，编写一个简单程序通过实际观察进行判断.为精确起见，采用多次循环运算观察运行时间.循环过程中va被赋予不同的值，取值为0.2～3.0，每个模型均做2 800 000次循环运算.程序用C++语言编写，在Athlon 1G/256M ram/Windows环境下调试运行，运行结果见图1(源程序详见附录).

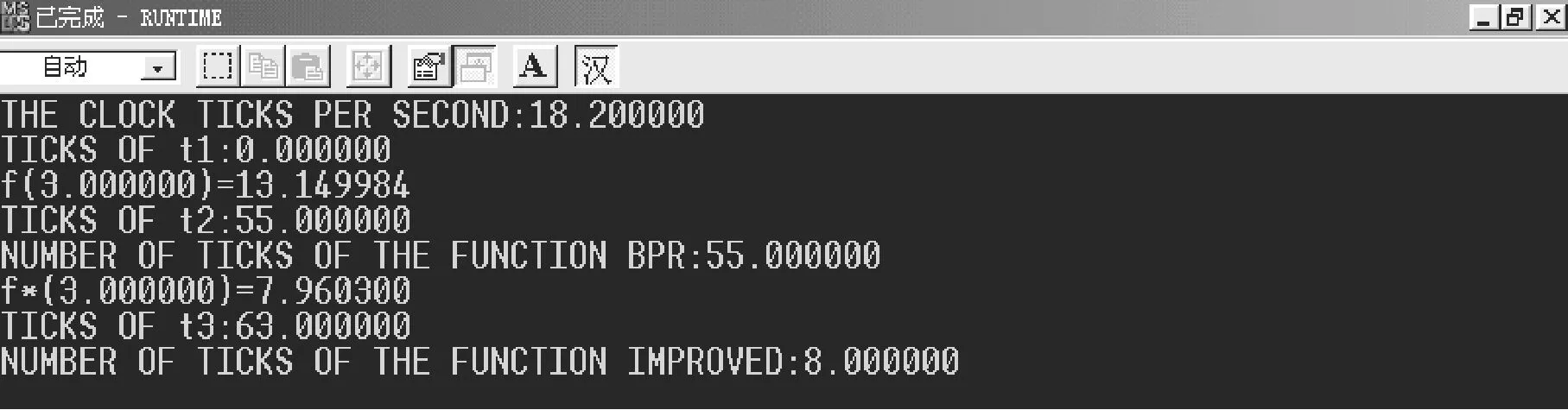
图1 BPR路阻模型和改进模型的程序运算时间

图1中18.2是机器每秒钟的时钟周期数，t1是程序开始运行时刻，t2是BPR函数循环完毕时刻，t3是改进函数循环完毕时刻.从图中可知BPR模型的运行时间为55个时钟周期，改进模型的运行时间为8个时钟周期.

为检验结果可信度，在不同的机型及系统环境下运行此程序，得到运行时间(单位：时钟周期)，见表1.从表中可以看出，改进的路阻函数在计算机内的运行时间明显小于BPR函数.

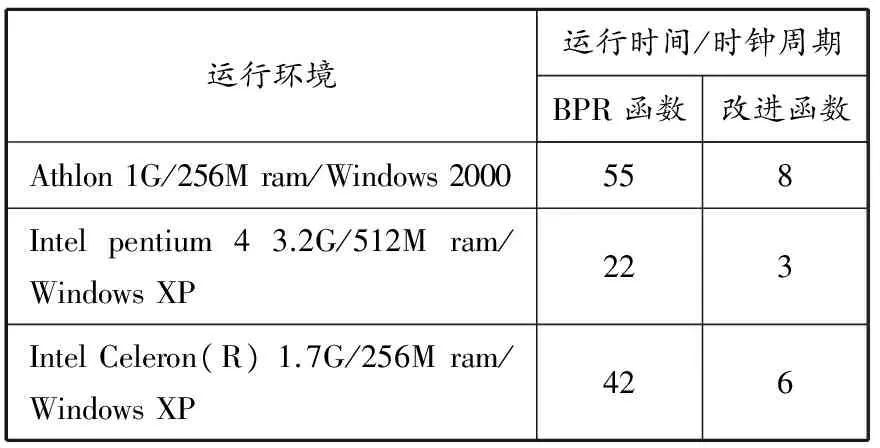
表1 不同运行环境下两函数运行时间对比

2 两种路阻函数的图像比较

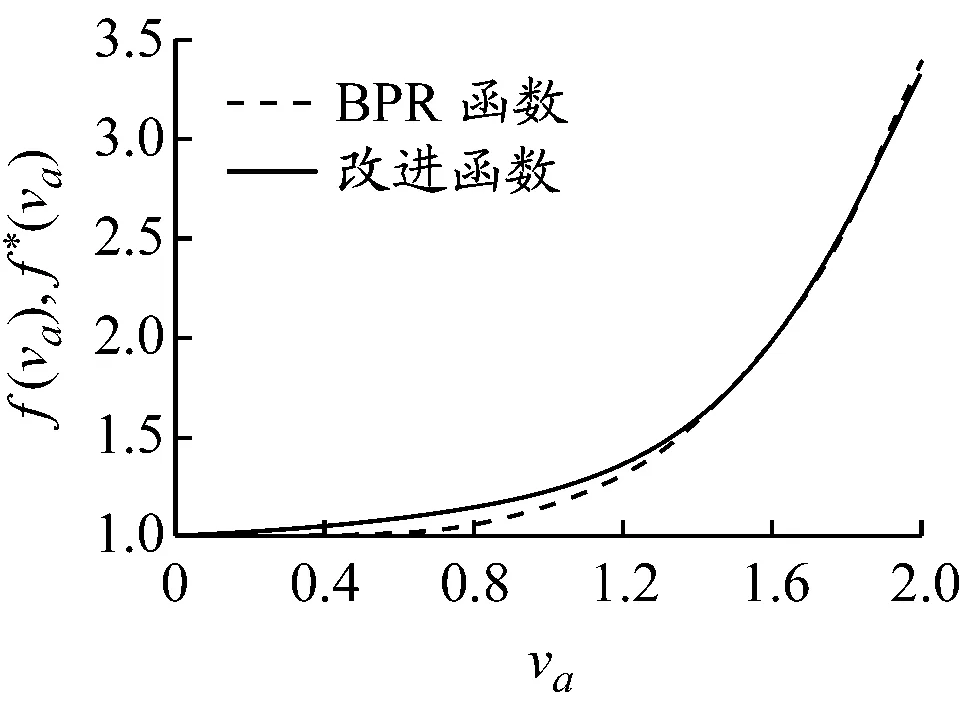
(a) β=4.0

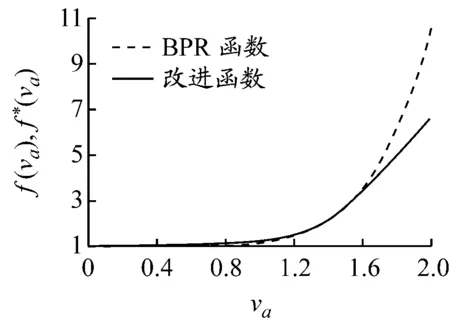
(b) β=6.0

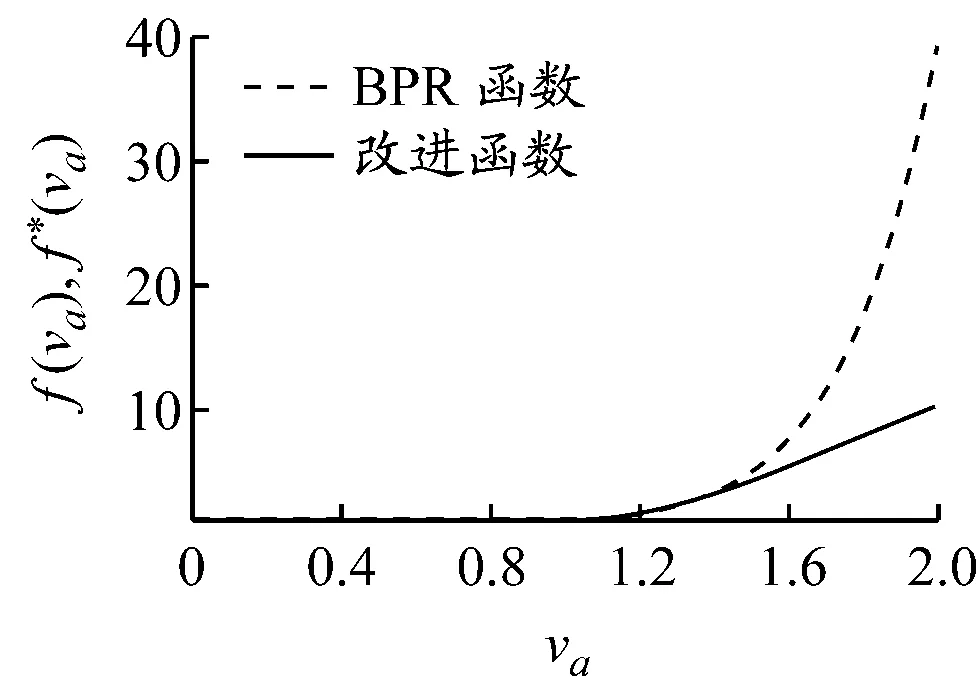
(c) β=8.0

(d) β=10.0

图3 α=0．15，β分别取不同值时两函数拟合情况 图4 β=4．0，α分别取不同值时两函数拟合情况

3 改进路阻函数模型在EMME软件中的应用

在宁波市鄞州区麦德龙交通影响分析项目中，参照《宁波市综合交通规划》的机动车需求预测[13]，采用BPR路阻函数通过交通分析软件EMME进行交通流分配，得到麦德龙周边地区主干路(钱湖北路和南外环路)的背景交通量预测，见图5.在各路段的参数取值相同的前提下，将BPR路阻函数改为改进的路阻函数再次配流，得到的预测结果见图6.

从图5和6可以看出，这两种配流结果比较接近.

图5 采用BPR函数时的配流情况 图6 采用改进函数时的配流情况

4 结束语

参考文献：

[1] 郑远, 杜豫川, 孙立军. 美国联邦公路局路阻函数探讨[J]. 交通与运输:学术版, 2007(1):1-2.

[2] Bureau of Public Roads. Traffic assignment manual[S].US Dept of Commerce, Urban Planning Division, Washington DC, 1964.

[3] 黎新华, 侯桂荣, 莫辉辉. 容量限制的分配优化方法研究[J].中南公路工程, 2005(4): 116-118.

[4] 刘桢根, 邓卫. 交通分布-交通分配组合模型研究[J]. 武汉理工大学学报:交通科学与工程版, 2006(6): 1031-1033.

[5] 王树盛, 黄卫, 陆振波. 路阻函数关系式推导及其拟合分析研究[J]. 公路交通科技, 2006(4): 107-110.

[6] 王元庆, 周伟, 吕连恩. 道路路阻函数理论与应用研究[J]. 公路交通科技， 2004(9): 82-85.

[7] 王炜, 徐吉谦, 杨涛, 等. 城市交通规划理论及其应用[M]. 南京:东南大学出版社, 1998: 72-74.

[8] 霍飞. 区域公路网路阻函数理论与应用研究[D].西安: 长安大学, 2012.

[9] XU Meng, SHI Zhongke. Outflow models based on velocity/density formulation used in dynamic traffic assignment[C]//Machine Learning and Cybernetics, Proc Int Conf, IEEE, 2005(6): 3568-3573.

[10] 刘灿齐, 陈军. 基于Edie模型的路阻函数关系推导及其拟合分析研究[J].交通标准化, 2012(4):33-36.

[11] 袁振洲. 动态交通分配中道路阻抗模型的研究[J]. 中国公路学报, 2002, 15(3): 92-101.

[12] SPIESS H. Technical note: conical volume-delay functions[J]. Transportation Sci, 1990, 24(2): 153-158.

[13] 刘旷, 夏晓梅, 董洁霜, 等. EMME在公路内外交通衔接规划中的应用[J].交通与运输:学术版, 2009(1): 18-21.

附录BPR路阻模型和改进模型运算时间源程序

include

include

include

main()

{

double a,b,c,d,x,y;

float t1,t2,t3;

clock_t clock();

a=0.15;

b=4;

c=(2*b-1)/(2*b-2);

d=pow(a,1/b);

printf("THE CLOCK TICKS PER SECOND:%f ",CLK_TCK);

t1=clock(); /*程序开始运行的时刻*/

printf("TICKS OF t1:%f ",t1);

for(x=0.2;x<=3;x=x+0.000001)

{

y=1+a*pow(x,b);

}

printf("f(%f)=%f ",x,y);

t2=clock(); /*BPR函数循环运行结束的时刻*/

printf("TICKS OF t2:%f ",t2);

printf("NUMBER OF TICKS OF THE FUNCTION BPR:%f ",t2-t1);

for(x=0.2;x<=3;x=x+0.000001)

{

y=2+sqrt(b*b*(1-d*x)*(1-d*x)+c*c)-b*(1-d*x)-c;

}

printf("f*(%f)=%f ",x,y);

t3=clock(); /*改进路阻函数循环运行结束的时刻*/

printf("TICKS OF t3:%f ",t3);

printf("NUMBER OF TICKS OF THE FUNCTION IMPROVED:%f ",t3-t2);

}