岸桥移动约束的连续泊位和岸桥集成调度
杜卫华, 黄有方, 杨斌, 孙玮珊
(上海海事大学 科学研究院,上海 201306)
0 引 言
泊位和岸桥是集装箱码头的两种紧缺资源,泊位分配问题(Berth Allocation Problem,BAP)和岸桥分配问题(Quay Crane Assignment Problem,QCAP)是集装箱码头运作优化领域的基本问题和热点问题.[1-3]部分学者将泊位分配和岸桥分配作为两个独立阶段进行研究.泊位分配中,首先根据船舶装卸箱量[4]、船舶靠泊位置[5-6]或平均装卸效率[7]等估算船舶作业时间,通过优化获得到港船舶的靠泊位置、靠泊时间及离港时间,且在分析时考虑泊位分配的性能指标,如船舶在港时间和码头运作成本的最小化,提高船舶装卸效率[8-9]等.岸桥分配的目标是确定服务每艘船舶的岸桥数和为船舶作业的岸桥集合.[10]因船舶作业时间与为其所分配的岸桥数直接相关,越来越多的学者开始将两个问题集成起来考虑,即根据船舶靠泊顺序、位置和可分配给船舶的岸桥数,通过靠泊计划和岸桥移动规则确定船舶作业开始时间和离港时间,最后得到泊位和岸桥分配方案.本文在集成调度方法的基础上给船舶最小最大岸桥分配数和限制岸桥频繁移动的约束,以达到减少岸桥移动次数和提高岸桥作业效率的目的.
泊位分配模型主要分两类:离散型泊位分配模型和连续型泊位分配模型.离散型泊位分配模型是把港口码头分割成几个小泊位的集合.NISHIMURA等[11]利用遗传算法求解离散泊位分配模型;IMAI等[12]在模型中给船舶设定不同的停泊优先顺序,设计启发式算法求解;KIM等[13]利用模拟退火算法求解离散泊位分配问题.连续型泊位分配模型将码头岸线看作连续的整体,按照船舶的长度依次进行停泊.IMAI等[14]利用启发式算法求解连续泊位分配模型;WANG等[15]将泊位分配问题看作多阶段决策问题,用随机束搜索算法求解.
关于岸桥调度模型的研究主要有:DAGANZO[16]建立使船舶延误成本最小的岸桥调度混合整数规划模型;KIM等[17]对单艘船舶作业的岸桥调度问题进行研究,分别采用分枝定界法和贪婪随机适应性搜索算法对模型进行求解;LEE等[18]建立岸桥调度整数规划模型优化岸桥作业的舱位顺序;TAVAKKOLI-MOGHADDAM等[19]建立岸桥配置与路径优化的混合整数规划模型,设计遗传算法求解;GOODCHILD等[20]建立岸桥双循环模型,减少岸桥空驶,提高岸桥作业效率.
事实上,泊位分配与岸桥调度是相互影响的,船舶靠泊作业时长基本上由所分配给它的岸桥数决定,所以泊位分配计划中要充分考虑岸桥的分配.同时,在岸桥作业过程中,也要依据泊位分配计划保证船舶按时离港.因此,对泊位和岸桥集成调度的研究越来越多:PARK等[21]建立同时优化船舶停泊位置、停泊时间及每艘船舶岸桥配置数的混合整数规划模型;IMAI等[22]采用离散泊位分配方法,建立同时优化泊位分配和岸桥调度的优化模型;LIANG等[23]建立泊位分配-岸桥调度模型,并加入岸桥配置数量对岸桥作业效率影响的约束.
1 模型建立
在IMAI等[14]和LIANG等[23]的基础上,建立泊位和岸桥集成调度混合整数规划模型,优化船舶的停泊位置、停靠时间、所分配的岸桥数和岸桥移动次数,以达到船舶延误成本最小和减少岸桥移动成本的目的.
模型采用连续型泊位分配,用“泊位-时间”[11]表示泊位分配方案;分配给船舶的岸桥数有最小值和最大值约束;服务某一船舶的岸桥可以在该作业未完成之前退出而转向其他相邻船舶的作业.
1.1 集合与参数
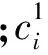
1.2 决策变量
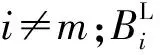
1.3 模型建立与优化
首先,通过式(1)~(19)建立泊位和岸桥集成分配模型(M1):
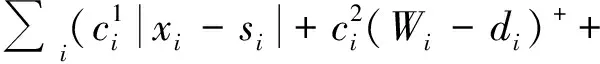
(1)
s.t. ∀i,m∈S,j∈N
xi+li≤L
(2)
yi≥ei
(3)
Wi≥yi+1
(4)
xi+li≤xm+L(1-Zi,m),i≠m
(5)
Wi≤ym+M(1-Xi,m),i≠m
(6)
1≤Zi,m+Zm,i+Xi,m+Xm,i≤2,
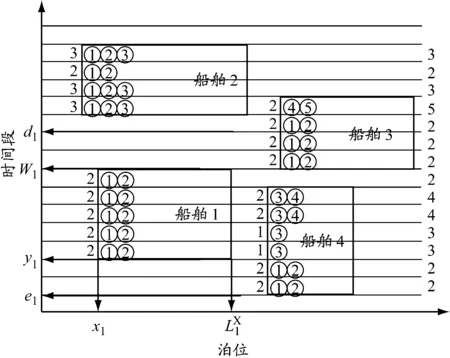
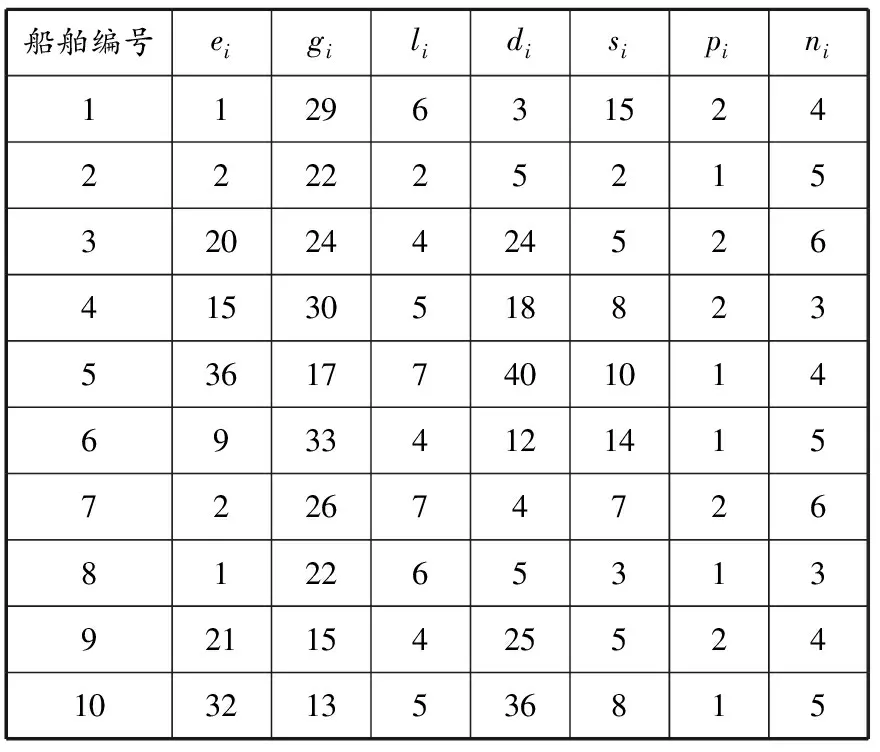
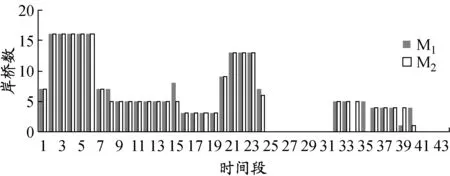
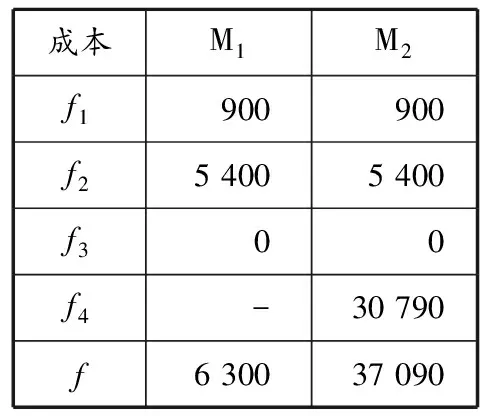
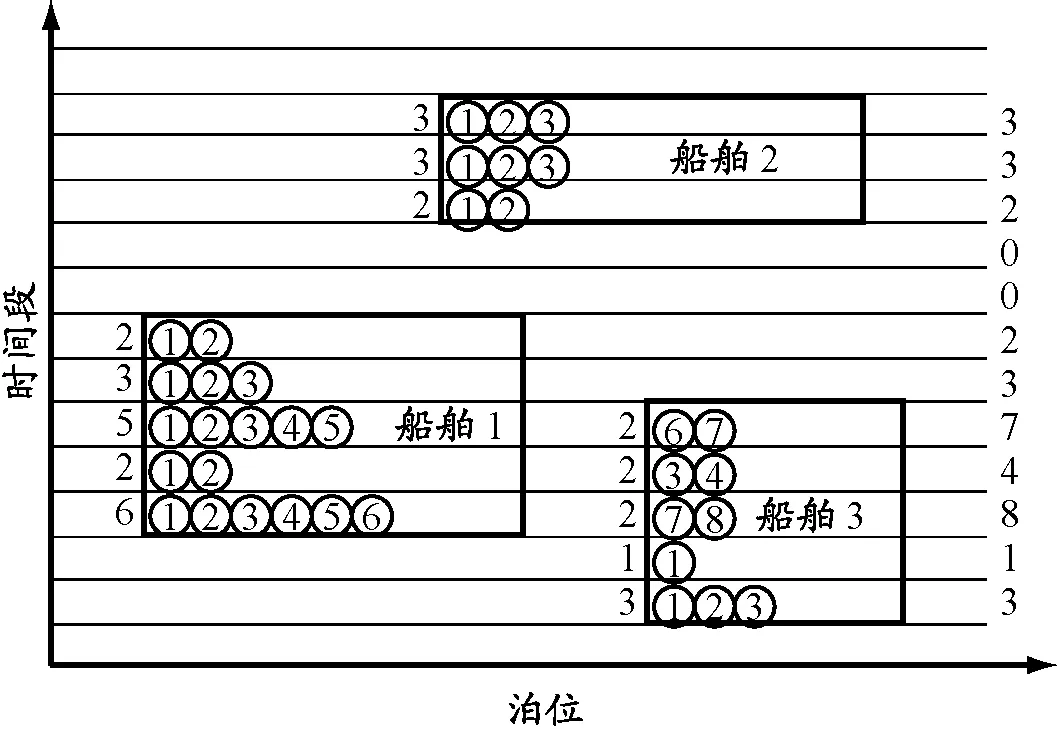
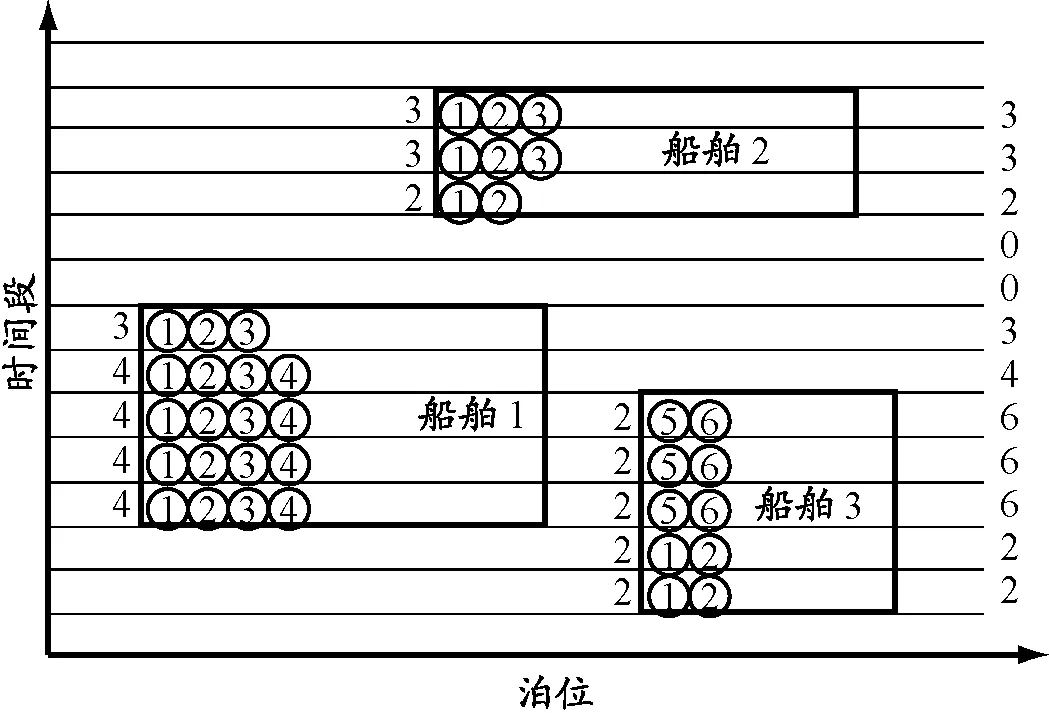
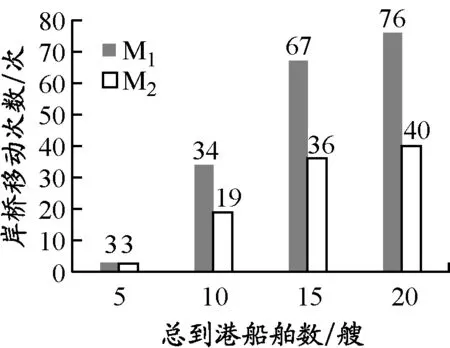
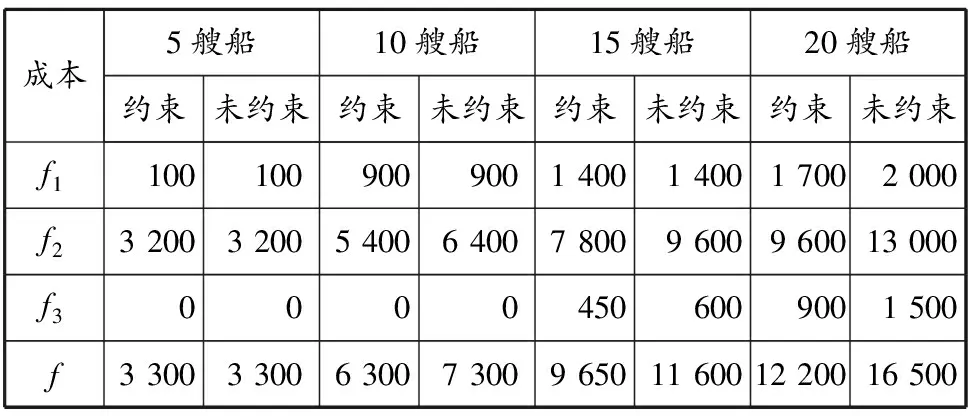
i (7) Wi≥Vi,j(j+1) (8) ∑iYi,j≤c (9) ∑jYi,j≥gi (10) Vi,j≤Yi,j (11) Yi,j≤MVi,j (12) ∑1≤j≤i*Yi,j=0, ∀i*∈N,1≤i*≤ei (13) Yi,j+M(1-Vi,j)≥pi (14) Yi,j≤ni (15) xi≥0 (16) Zi,m,Xi,m∈{0,1},i≠m (17) Vi,j∈{0,1} (18) (Wi-di)+=max(Wi-di,0) (19) 图1 泊位-时间时空图示例 在建立的泊位岸桥集成调度模型(M1)中未对岸桥的移动加以限制,导致一些船舶靠泊作业时岸桥移动过于频繁,甚至出现作业暂停(即开始作业后的某时间段内分配给船舶的岸桥数为0).虽然这样可以最大限度地利用已有岸桥资源,加快整个码头作业,但是岸桥频繁移动会导致岸桥使用效率降低.为避免这种现象,在M1基础上加入限制岸桥频繁移动的约束条件,同时考虑由于岸桥频繁移动引起的效率下降的成本,建立基于岸桥移动约束的泊位和岸桥集成调度模型(M2),其目标函数及式(1)~(19). 式(20)为以偏离偏好位置靠泊成本f1,延迟离港处罚成本f2,等待泊位时间处罚成本f3及岸桥移动成本f4最小定义的港口运营成本目标函数;式(21)和(22)表示通过控制Wi,j*的值提高岸桥使用率. 表1 船舶参数 根据表1中数据,运用Cplex软件分别求解模型M1和M2,得到这两个模型在每个时间段的岸桥使用数量,见图2;表2为分别采用这两个模型所得到的最优解中的成本,其中f为总成本. 在港口码头,船舶上的岸桥作业时间基本是固定的,一艘船舶作业时间只与作业的岸桥数有关.从图2可以看出,除在第8,15,24,34,35,39,40个时间段内岸桥使用数不一致外,其他时间段的岸桥使用数都是一致的.这说明这两个模型的岸桥使用数在各时间段是基本一致的,岸桥总的作业时间基本没有变化,对作业效率没有太大影响,由此可知两个模型中岸桥作业时间和作业效率在整个港口作业过程中没有太大区别.另外,由表2列出的成本明细可知,在两个模型计算出的最优解中f1,f2和f3相同,不同的是f4,这说明新模型在加入限制岸桥频繁移动条件后,并没有增加不考虑岸桥移动模型的成本. 图2 模型M1和M2在各时间段内的岸桥使用数对比 表2模型M1和M2的成本明细对比 成本M1M2f1900900f254005400f300f4-30790f630037090 图3 优化前岸桥移动次数示例 图4 优化后岸桥移动次数示例 在岸桥作业时,移动过于频繁会使其使用效率大大降低,岸桥调度也会更加繁琐和复杂.岸桥移动分为轨道式和轮胎式,其移动路线基本固定或变化非常小,岸桥移动过于频繁会极大地增强岸桥之间的相互干扰,增加管理成本.当干扰较大时往往会带来更多的人工成本和其他管理成本,同时增加船舶靠泊成本.如图3所示,服务船舶1的岸桥最初是6个岸桥,后变为2个、5个、3个和2个,导致岸桥要离开船舶1,这就涉及岸桥的频繁移动.假设服务船舶k的岸桥因作业而移动的总次数为Qk(第一次和最后一次岸桥移动不计算在内),以图3中船舶1,2,3为例,Q1=|2-6|+|5-2|+|3-5|+|2-3|=10,同理Q2=1,Q3=3. 在有预见性的情况下,可以通过模型M2优化后,达到类似图4的调度策略,在不增加运营成本的前提下极大地减少岸桥移动次数和岸桥利用率.此时Q1=1,Q2=1,Q3=0. 对Cplex软件得出的数据进行进一步整理计算可得,模型M1中所有岸桥移动总次数为34次,而在模型M2中所有岸桥移动总次数为19次.由此可见,加入限制岸桥频繁移动约束条件能大大降低岸桥移动次数,提高岸桥使用效率,降低岸桥调度难度并简化岸桥移动计划,从某种程度上会减少岸桥移动中出现混乱或其他干扰因素的机会,避免多船舶出现时大幅度岸桥调度或没有岸桥为船舶服务的现象.在算例中,模型M1中出现在船舶连续的时间段内岸桥变化为4→1→4,移动次数为6次,变化幅度很大,甚至出现5→0→5,移动次数为10次,这表示在中间那一时刻没有岸桥为船舶服务,经过对模型优化,加入限制岸桥频繁移动条件,相关船舶岸桥调度变为4→4→1,5→5→5,岸桥移动次数分别为3次和0次,减少岸桥移动次数,使得调度更加合理.为充分说明加入限制岸桥频繁移动约束的合理性与正确性,分别计算5艘船、10艘船、15艘船、20艘船在两个模型中的结果,见图5.从图中可以明显看出,当船舶数量大于5时,M2模型中岸桥移动次数明显减少,4种情况下移动次数分别减少0,44.1%,46.2%和47.4%.因此可以合理预见当靠泊船舶数量越多时,M2模型相对于M1模型的优越性会越明显,减少岸桥频繁移动的次数会越多. 图5 采用模型M1和M2岸桥移动次数对比 对不同的船舶数量所得的岸桥调度计划中,加入限制岸桥频繁移动约束后,岸桥移动次数一直都相对较小,并且f1,f2和f3在两个模型中的值没有变化.这充分说明加入限制岸桥频繁移动约束的新模型使得岸桥移动次数更少,岸桥利用率更高,岸桥调度更为合理,而且随着船舶数量增加,限制岸桥频繁移动效果显著. 在成本方面,如果不考虑模型M2中的约束条件(21)和(22),即考虑岸桥移动但对岸桥的移动不加以限制,会增加船舶在港时因岸桥的频繁移动带来的额外成本,甚至可能影响到船舶到港后的靠泊和船舶到港、离港时间变化,造成f1,f2和f3的增加.在模型M2中去除约束条件(21)和(22)后分别对5艘船、10艘船、15艘船、20艘船的靠泊计划进行计算,其结果与有约束条件的结果的对比见表3. 表3 有约束与无约束条件的成本对比 泊位岸桥集成调度是一个同时处理合理泊位分配和岸桥调度的多目标任务,岸桥的作业效率和岸桥利用率是决定岸桥对船舶服务时间的两个重要因素.针对连续的泊位分配和岸桥调度的动态协调问题,在最大限度利用已有岸桥资源加快整个港口码头作业的同时,减少岸桥的频繁移动以提高岸桥使用效率.本文在研究泊位和岸桥集成调度时以限制岸桥频繁移动为约束,建立以船舶总在港惩罚成本最小为目标函数的混合整数规划模型,并通过试验算例验证其合理性与正确性.算例分析表明,本文提出的方法可以:(1)在船舶靠泊规模大于5艘时提高岸桥实际使用效率40%以上;(2)减少当多艘船出现时因岸桥频繁移动造成的岸桥之间的相互干扰;(3)防止出现在船舶未装卸完之前没有岸桥为其服务的情况;(4)减少考虑岸桥移动但未限制岸桥频繁移动而带来的额外成本;(5)提高港口码头对岸桥和船舶的管理效率.本文虽然考虑岸桥频繁移动带来的代价,但对该代价并没有提出具体的计算方法,同时也没有考虑这个因素与岸桥作业的其他因素之间的耦合关系.通过与港口合作,了解岸桥移动的规律和岸桥移动产生的成本,能够使这个模型更接近集装箱码头的实际情况,具有更强的实用性. 参考文献: [1] BIERWIRTH C, MEISEL F. A survey of berth allocation and quay crane scheduling problems in container terminal[J]. Eur J Operational Res, 2010, 202(3): 615-627. [2] STEENKEN D, VOβ S, STAHLBOCK R. Container terminal operation and operations research: a classification and literature review[J]. OR Spectrum, 2004, 26(1): 3-49. [3] STAHLBOCK R, VOβ S. Operations research at container terminals: a literature update[J]. OR Spectrum, 2008, 30(1): 1-52. [4] GUAN Y, CHEUNG R K. The berth allocation problem: models and solution methods[J]. OR Spectrum, 2004, 26(1): 75-92. [5] AKIO I, ETSUKO N, MASAHIRO H,etal. Berth allocation at indented berths for mega-container vessels[J]. Eur J Operational Res, 2007,179(2): 579-593. [6] IMAI A, NISHIMURA E, PAPADIMITRIOU S. Berthing ships at a multi-user container terminal with a limited quay capacity[J]. Transportation Res Part E, 2008, 44(1):136-151. [7] CORDEAU J F, LAPORTE G, LEGATO P,etal. Models and tabu search heuristics for the berth allocation problem[J]. Transportation Sci, 2005, 39(4): 526-538. [8] 何军良, 宓为建, 谢尘, 等. 基于分布式混合遗传算法的动态泊位分配策略与仿真[J]. 上海海事大学学报, 2008, 29(2): 52-57. [9] 乐美龙, 陈雷雷, 黄有方. 集装箱港口动态泊位指派仿真优化[J]. 上海海事大学学报, 2013, 34(1): 23-27. [10] 董良才, 丁以中, 宓为建. 基于时间窗的集装箱装卸桥调度[J]. 上海海事大学学报, 2011, 32(1): 1-7. [11] NISHIMURA E, IMAI A, STRATOS P. Berth allocation planning in the public berth system by genetic algorithms[J]. Eur J Operational Res, 2001, 131(2): 282-292. [12] IMAI A, NISHIMURA R, STRATOS P. Berth allocation with service priority[J]. Transportation Res Part B, 2003, 37(5): 437-357. [13] KIM K H, MOON K C. Berth scheduling by simulated annealing[J]. Transportation Res Part B, 2003, 37(6): 541-560. [14] IMAI A, SUM X, NISHIMURA E,etal. Berth allocation in a container port: using a continuous location space approach[J]. Transportation Res Part B, 2005, 39(3): 179-221. [15] WANG F, LIM A. A stochastic beam search for the berth allocation problem[J]. Decision Support Systems, 2007, 42(4): 2186-2196. [16] DAGANZO C F. The crane scheduling problem[J]. Transportation Res Part B, 1989, 23(3): 159-175. [17] KIM K H, PARK Y M. A crane scheduling method for port container terminals[J]. Eur J Operational Res, 2004, 156(3): 752-768. [18] LEE D H, WANG H Q, MIAO L. Quay crane scheduling with non-interference constraints in port container terminals[J]. Transportation Res Part E, 2008, 44(1): 124-135. [19] TAVAKKOLI-MOGHADDAM R, MAKUI A, SALAHI S,etal. An efficient algorithm for solving a new mathematical model for a quay crane scheduling problem in container ports[J]. Computers & Ind Eng, 2009, 56(1): 241-248. [20] GOODCHILD A V, DAGANZO C F. Crane double cycling in container ports: planning methods and evaluation[J]. Transportation Res Part B, 2007, 41(8): 875-891. [21] PARK Y M, KIM K H. A scheduling method for berth and quay cranes[J]. OR Spectrum, 2003, 25(1): 1-23. [22] IMAI A, CHEN H C, NISHIMURA E,etal. The simultaneous berth and quay crane allocation problem[J]. Transportation Res Part E: Logistics Transportation Rev, 2008, 44(5): 900-920. [23] LIANG C, HUANG Y, YANG Y. A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning[J]. Computers & Ind Eng, 2009, 56(3): 1021-1028.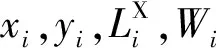
2 算例与分析
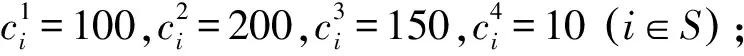
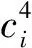
3 结束语

