基于逆散射级数法的鬼波压制方法

王芳芳，李景叶，陈小宏

1 中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249

2 中国石油大学CNPC物探重点实验室，北京 102249

1 引 言

在海洋地震勘探中，需要将震源和接收器放置于海平面以下一定深度，由于海水与空气波阻抗差异较大，两者之间形成了较强的反射面而构成自由表面，使震源处激发的地震波经过该自由表面再向下反射，形成鬼波．鬼波的波形、频率、视速度等都与一次反射波相似，从而严重干扰一次反射波，降低地震剖面的分辨率，有时甚至会产生假的同相轴，给地震资料反演与地质解释造成很大的困难［1］，甚至产生错误的解释结果．因此，鬼波压制是海上地震资料处理最重要的步骤之一．

鬼波压制是勘探地球物理界研究的重点之一，国内外许多学者在该领域做了颇有成效的研究工作［1－5］．基于地震记录是反射波与鬼波滤波器的褶积的假设，可以将消除鬼波的方法分为时间域鬼波压制方法和频率域鬼波压制方法．前者是基于最优化的反褶积处理过程，但由于鬼波的振幅谱上存在一系列的“零值点”，说明它不是最小相位的，因此应用时间域反褶积处理不能完全消除鬼波［6］．后者是在不包含“零值点”的频带内去除鬼波算子，但为了获得较好的压制效果，方法要求地震记录有效频宽内不包含鬼波滤波器振幅谱的“零值点”，这将增加野外信息采集的难度，尤其对高分辨率地震勘探更加难以实现［6］．对于二维情况，Katibe等［7－8］给出了频率－波数域内消除鬼波算法．上述方法是基于鬼波与一次反射波存在时差的特性提出的，压制时需要预先精确地求取鬼波延迟，但对于实际采集条件和多维介质，准确的鬼波延迟往往难以获取．Weglein等［9］首先提出了基于格林定理的鬼波压制方法，该方法是在一定深度范围内估计波场的法向导数，它只需要波场数据便可以进行鬼波压制，但该方法依赖于对波场的法向导数估计的精度．Zhang 和Weglein［10］改进了基于格林定理的鬼波压制算法，但这种方法需要预先估计子波．Mayhan［11］等利用基于格林定理的鬼波压制方法进行了实际资料处理，获得了不错的结果，但方法需要压力场数据及其法向导数数据．基于格林定理的鬼波压制方法，对鬼波的描述是精确的，适用于多维复杂介质，但算法要求对波场法向导数数据或者子波进行估计，应用范围受限．

逆散射级数理论起源于量子力学领域，该方法通过研究散射体外部接收到的各种场来估计其内部结构信息［12］．Moses［13］由反射系数推导了量子散射势的级数表达式；Prosse［14］研究了Moses提出方法的收敛性；Razavy［15］提出根据反射系数来恢复速度场．Weglein等［16］将该理论引入到地球物理勘探中，并应用于多次波压制及成像等方面［16－17］．Weglein（1997）完整表述了将散射级数分离成面向不同目标的子级数这一思想，将散射级数分离成分别与鬼波相关、与自由表面多次波相关和与层间多次波相关的子级数，并提出了基于逆散射级数法（ISS）的鬼波和表面多次波压制方法［12，18］．在国内，金德刚［19］证明采用逆散射级数方法进行鬼波压制理论是完善的．李翔等和刘华锋［20－21］在基于逆散射级数压制鬼波算法方面开展了研究工作，取得了一定进展．基于逆散射级数鬼波压制方法以波动方程和Lippmann－Schwinger方程为理论基础，对鬼波的描述是精确的，适用于多维复杂介质，并且不需要预先对鬼波延迟时差或者子波等进行估计，方法具有很好的应用前景．研究针对逆散射级数压制鬼波算法，通过在频率－波数－波数域内对鬼波振幅谱“零值点”进行约束，改善鬼波压制算子，提高鬼波压制效果．模型资料处理与效果分析证明，研究方法较好的实现了鬼波压制，补偿地震资料低频损失，恢复了地震记录的有效频谱，提高地震数据的保真度．

2 方法原理

散射理论是扰动分析的一种．广义上，它描述了介质性质的扰动与其引起的波场扰动之间的关系．一般把初始未扰动的介质称为参考介质，实际介质与参考介质的差异称为扰动介质，扰动介质可以用扰动算子表示，震源通过实际介质产生的波场与震源通过参考介质产生的波场之间的差异为散射场．散射正演通过研究扰动算子来获取散射波场的信息，而逆散射问题则是从散射波场出发，分析研究扰动算子的性质，进而获得实际介质的信息．从参考介质和实际介质的单频微分方程出发定义散射场和扰动算子，假设震源与接收点的影响已经消除了，可得到格林函数对应的波动方程：

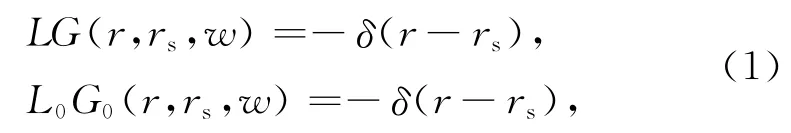
式中，L，L0，G（r，rs，w）和G0（r，rs，w）分别表示实际波场和参考波场在某一瞬时频率w下的微分算子及格林函数，G（r，rs，w）和G0（r，rs，w）简写为G、G0．δ（r－rs）是狄拉克函数，r、rs分别是波场内的任一点与震源点．

扰动算子V和散射波场算子Gs定义为

L，L0，V对于不同介质具体表达式不同．对于非均匀声波介质而言，对应地L，L0，V分别是：

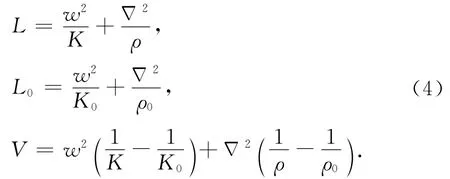
根据Lippmann－Schwinger方程，可以得到Gs与G、G0及V之间的方程：

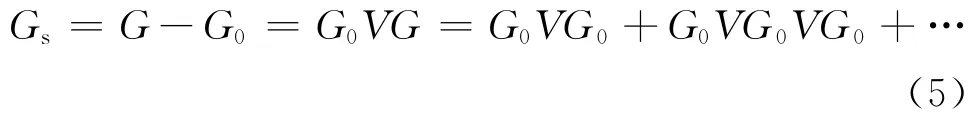
定义D为散射场Gs在观测表面上记录的数据，并将扰动算子V用级数形式展开，则得到

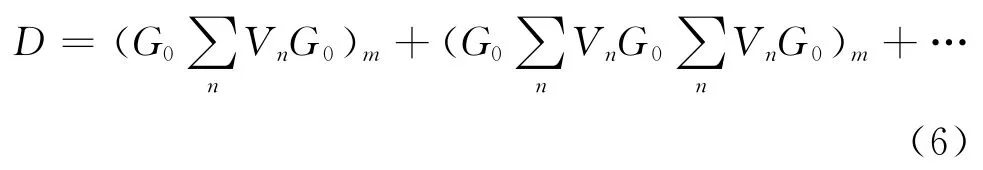
其中，（）m表示对震源、接收点所在平面积分．可以从散射数据D推导各个子级数V1、V2等，推导得到V的过程即为逆散射理论．从物理意义上讲，逆散射求解V的过程也即求解实际介质与参考介质性质差异的空间分布过程．

逆散射理论通常假定介质的扰动在观测界面的一侧．在地震应用中，该条件转换为震源－接收界面以下实际介质和参考介质存在差异，而在震源－接收界面以上两者一致．因此对于海洋地震勘探而言，选择以气－水分界面为自由表面的半空间水为参考介质，气－水分界面位置在z＝0处．海洋地震模型及其参考介质的格林函数的构成如图1所示，该参考场对应的格林算子G0，包括两部分：

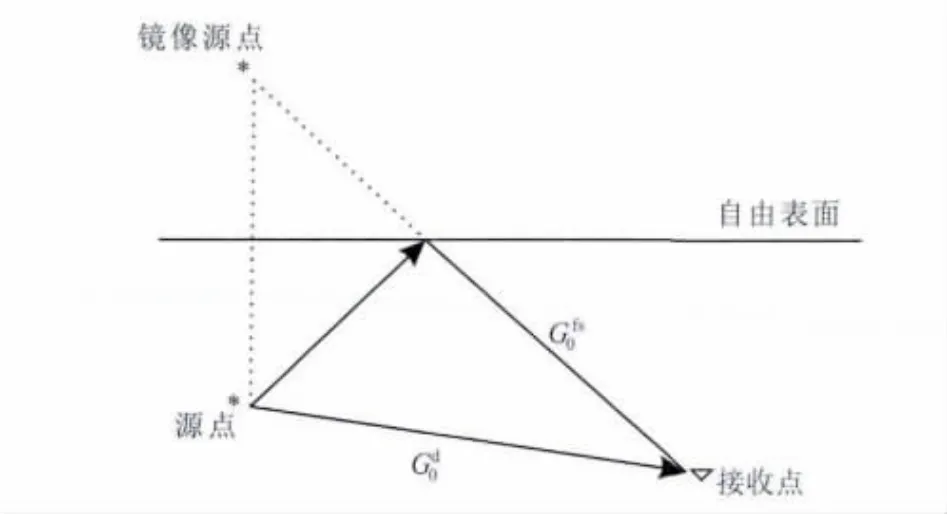
图1 海洋地震模型及其参考介质的格林函数的构成Fig．1 Marine configuration and reference Green function

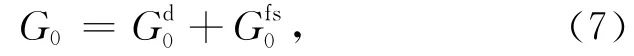
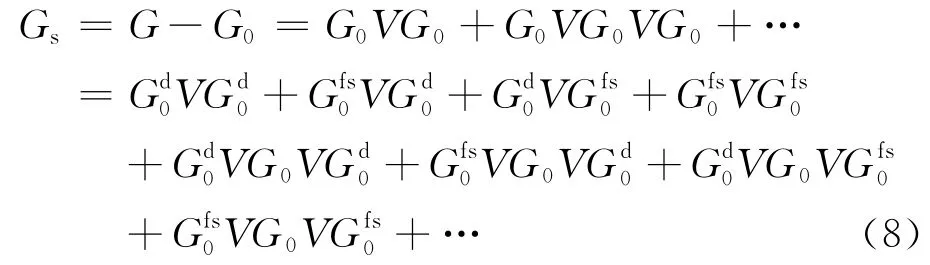
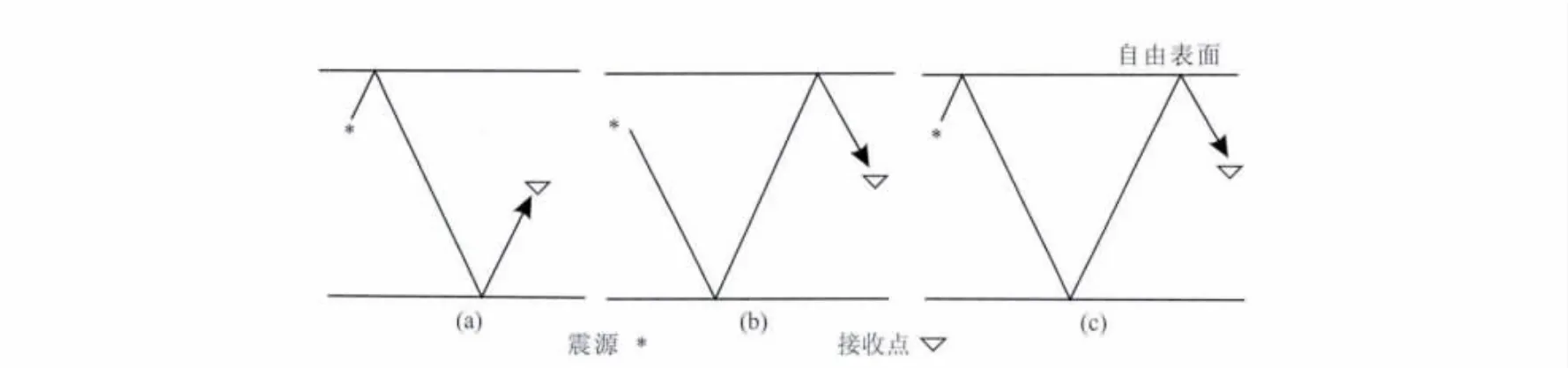
图2 三种类型的鬼波示意图（a）源点型鬼波；（b）接收点型鬼波；（c）混合型鬼波．Fig．2 Sketch of ghost events（a）Source ghost；（b）Receiver ghost；（c）Source－receiver ghost．

因此，不包含鬼波的散射场公式可以表示为

其中G′s为压制鬼波后的数据．为了得到G′s，实现鬼波压制，推导式（8）可以得到

上式即为基于逆散射级数鬼波压制方程．而由式（9）得到式（8）的过程即为产生包含鬼波地震记录的过程：

级数的收敛性是计算级数时非常重要的问题之一．对于完整的逆散射级数，其收敛性所需满足的介质条件比较严格．为了将逆散射级数理论应用到鬼波压制中，Weglein［18］提出从完整子级数选择出面对鬼波压制的子级数，当满足该子级数的收敛条件时，可应用子级数进行鬼波压制．对于鬼波压制，当选择半空间水体为参考介质时，该子级数满足收敛条件．

为实现海上基于逆散射级数鬼波压制，对方程（10）具体算法进行详细推导，选择以气－水分界面为自由表面的水为参考介质，气－水分界面位置在z＝0处，震源与接收点分别位于（xs，zs），（xg，zg）处，（x，z）为2D空间内任一点，则参考介质算子L0满足：

式中，ρ0 为参考介质的密度，κ0为参考介质的体积模量．对该方程关于x作傅里叶变换得到，数据由频率域变换到频率－波数域：

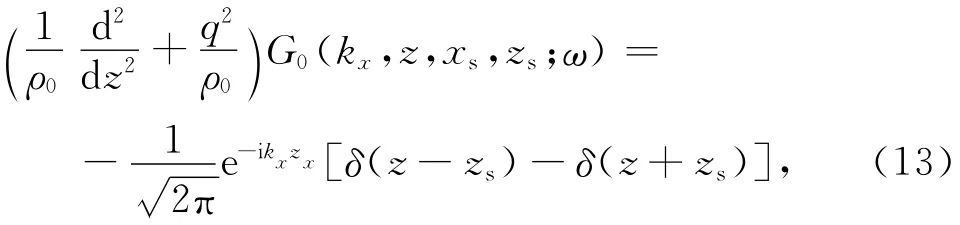
求解方程（13）可以得到参考场格林算子：

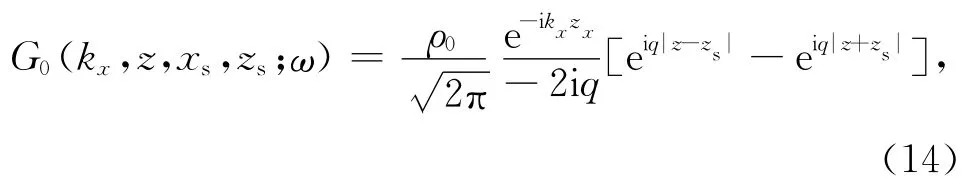
式中，kx为水平波数，q＝为垂直波数，为海水的纵波速度．

而参考场中由震源传播到各个散射点对应场的格林算子：

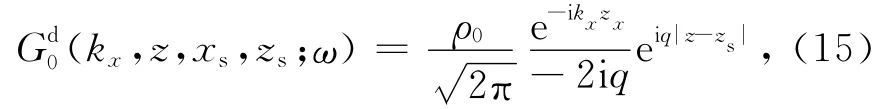
D为散射场GS在观测表面上记录的数据，D满足：

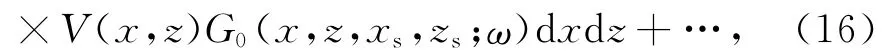
对该方程关于xg、xs做傅里叶变换：

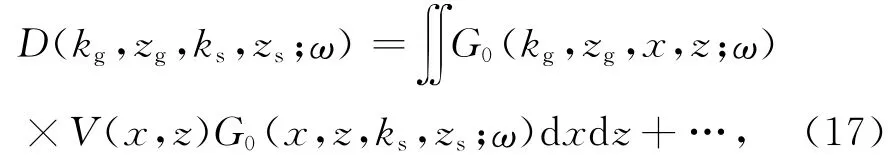
则鬼波压制后的数据D′为

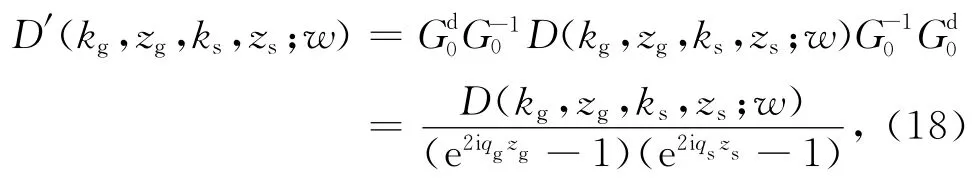
则得到包含鬼波的数据D为

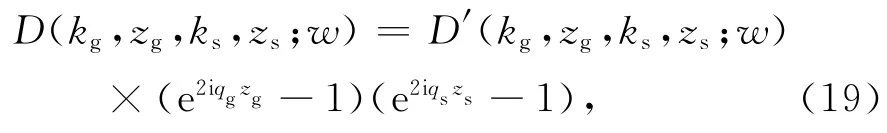
式中，qg＝sgn（ω）、qs＝sgn（ω）×分别为对应于kg、ks垂直波数．

为了便于表述，记Q＝（e2iqgzg－1）（e2iqszs－1）．在鬼波压制过程中，Q会出现零值，使得1/Q奇异，影响鬼波压制算法计算的稳定性．而只选择性处理Q的非零区域，将会带来视速度约为c0的线性干扰．因此，需要对1/Q进行稳定性处理，研究引入白噪因子，如公式（20）所示，从而实现方程的稳定求解：

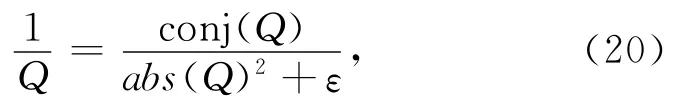
其中，ε为白噪因子，取值范围可以为0．01～0．1．

结合逆散射级数法压制鬼波的原理分析及对模拟数据处理过程与效果分析，研究建立了压制鬼波流程：（1）对炮集记录，切除直达波，得到散射场地震数据；（2）选择合适插值方法实现近偏移距地震数据补偿；（3）进行地震数据规则化处理，恢复缺失道、坏道地震数据；（4）按照公式（18）进行鬼波压制，得到鬼波压制后的地震数据．

3 数据处理试验

3．1 简单模型数据

为了验证基于逆散射级数鬼波压制方法的有效性，首先对简单模型模拟地震数据进行处理试验与效果分析．采用的模型由三层层状介质组成，而观测系统采用单边放炮单边接收，炮间距和道间距均为3m，震源深度6 m，接收点深度6 m，采样间隔2ms，记录时长1024ms．

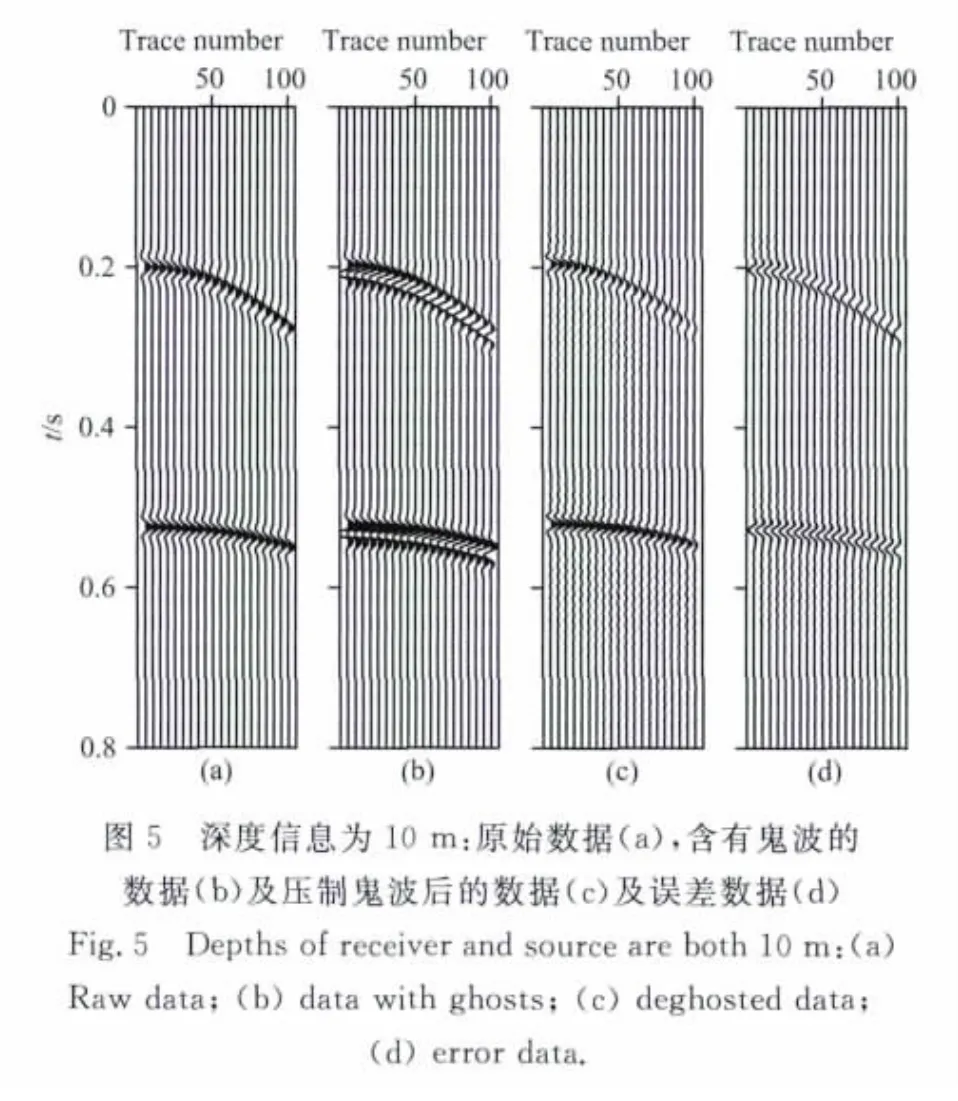
图3a为合成的只有一次反射波没有鬼波的地震数据，3b为合成的含有鬼波的地震数据，3c为压制鬼波后的地震数据，3d为误差数据．从图3b可以看出，由于鬼波的影响，一次波的波形发生了变化，振幅极大值点均偏离了实际的界面．图3c表明采用本文研究方法进行鬼波压制后，一次波的时间、振幅、相位都得到了很好的恢复，证明了方法的有效性．图3d误差数据数值较小，表明压制鬼波后与真实数据振幅、相位差异较小．

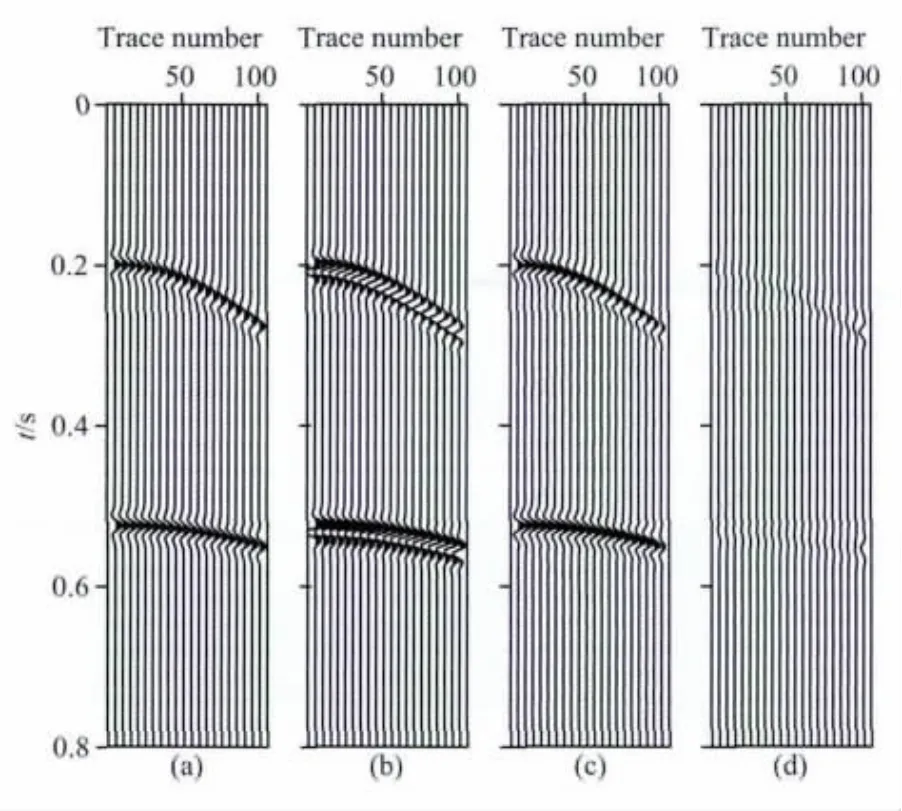
图3 深度信息精确时原始数据（a），含有鬼波的数据（b），压制鬼波后的数据（c）及误差数据（d）Fig．3 Real depths of receiver and source（a）raw data；（b）data with ghosts；（c）deghosted data；（d）error data．

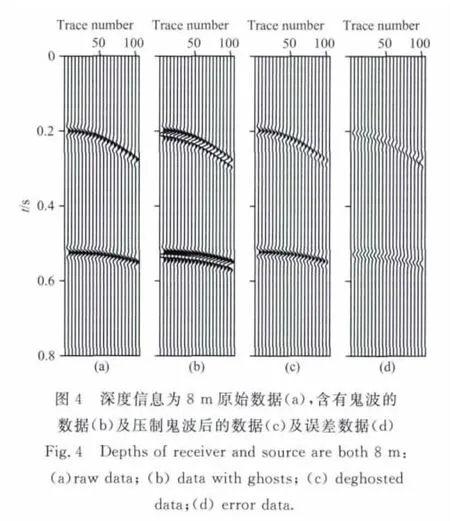
基于逆散射级数鬼波压制方法需要输入震源、接收点的深度信息，研究基于模拟资料对深度信息的敏感性进行测试．对于合成数据，震源、接收点的准确深度为6 m，下面分别将两个深度改用8 m、10m进行计算，计算处理结果分别如图4和图5所示．分析图4数据表明当深度信息误差较小时，一次波形态能基本恢复，但是误差数据已明显增大．分析图5数据可以看出，当深度信息误差较大时，压制鬼波同时会引入假的信息，误差数据比较大，降低了地震剖面的质量．因此深度信息越精确鬼波压制效果越好．实际海上地震采集深度信息误差一般在允许范围内，因此可以利用该方法进行鬼波压制．为了验证研究方法的抗噪性，在原始模拟地震数据中加入了高斯噪声，按照地震资料信噪比定义S/N＝A1/A2（其中A1为原始信号的能量，A2为噪声的能量），计算地震资料信噪比约为1，然后利用研究方法进行的鬼波压制效果如图6所示．图6数据分析表明在信噪比较低的情况下，研究方法仍能有效压制鬼波，说明方法可以进行低信噪比资料处理．图7为鬼波压制前后频谱对比图，其中红色曲线为原始无噪数据，蓝色曲线为含有鬼波的地震数据，黑色曲线为压制鬼波后的地震数据．从频谱对比图上可以看出，由于鬼波的存在降低了地震数据的低频信息，同时也带来一些假的高频信息，鬼波压制后恢复了低频信息，同时压制了假的高频信息．

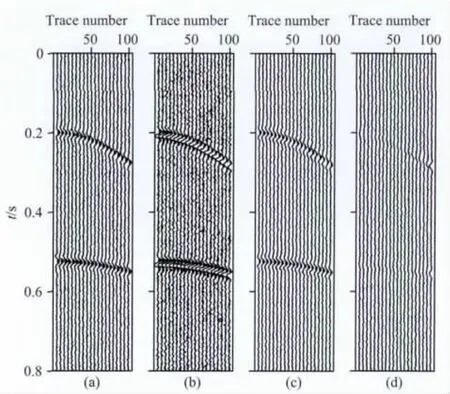
图6 S/N＝1时原始数据（a），含有鬼波的数据（b）及压制鬼波后的数据（c）及误差数据（d）Fig．6 S/N＝1：（a）Raw data；（b）data with ghosts；（c）deghosted data；（d）error data．

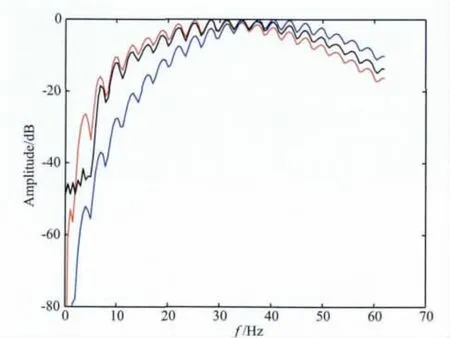
图7 频谱对比分析图原始数据（红色），含有鬼波的数据（蓝色），压制鬼波后的数据（黑色）Fig．7 Comparison between amplitude spectrum of originalshot gather（red）；shot gather with ghosts（blue）and deghosted shot gather（black）．

3．2 复杂模型数据

为了进一步验证研究方法的有效性，应用逆散射级数压制鬼波方法对基于SMARRT Pluto模型合成的地震数据进行处理试验．模拟地震数据采用单边放炮单边接收的规则观测系统，炮点及检波点深度均为7．62m，炮间距和道间距均为22．86m，每道采样点数为1126个，采样率为8ms，每炮361道，共选用1178炮数据．

研究首先进行直达波切除，直达波切除后的单炮地震数据，如图8a所示，图8b为压制鬼波后的单炮地震数据．图9（a，b）分别为图8（a，b）中红色框中的局部放大图．从单炮记录和叠加剖面都能清晰看出鬼波的影响．从图8a和图9a中可以看出由于鬼波的存在，一次波的波形发生了改变，其旁瓣较多，并产生了假的同相轴，如图9a中3．15s处所示．将切除直达波后炮集记录作为原始输入，进行鬼波压制处理，压制鬼波后的单炮数据如图8b所示．对比分析图8（a，b）可以看出，压制鬼波后子波的旁瓣减少，波形得到恢复，同相轴变少而清晰，地震资料质量明显提高．对比分析图9（a，b）可以看出，图9b中3．15s处的同相轴得到了压制，真实同相轴得到了恢复，尾随在一次波之后的鬼波得到了压制．图10为压制鬼波前后地震资料的频谱图，频谱数据对比分析表明，地震资料低频成分得到有效恢复，假的高频信息得到压制．图11（a，b）及图12（a，b）依次为压制鬼波前后的叠加剖面及其局部放大图．图12a中2．92s、3．08s处的波形得到了有效恢复，2．97s处假的同相轴得到了压制，一次波的波形得到了有效恢复．结果表明压制鬼波后同相轴变少，有效反射波得到较好恢复，地震资料质量明显提高．

图8 SMAART模型去除鬼波前后的炮集对比图（a）原始单炮记录；（b）鬼波压制后的记录．Fig．8 Comparison between original shot gather and deghosted shot gather of SMAART（a）is an original shot gather，（b）is deghosted shot gather．

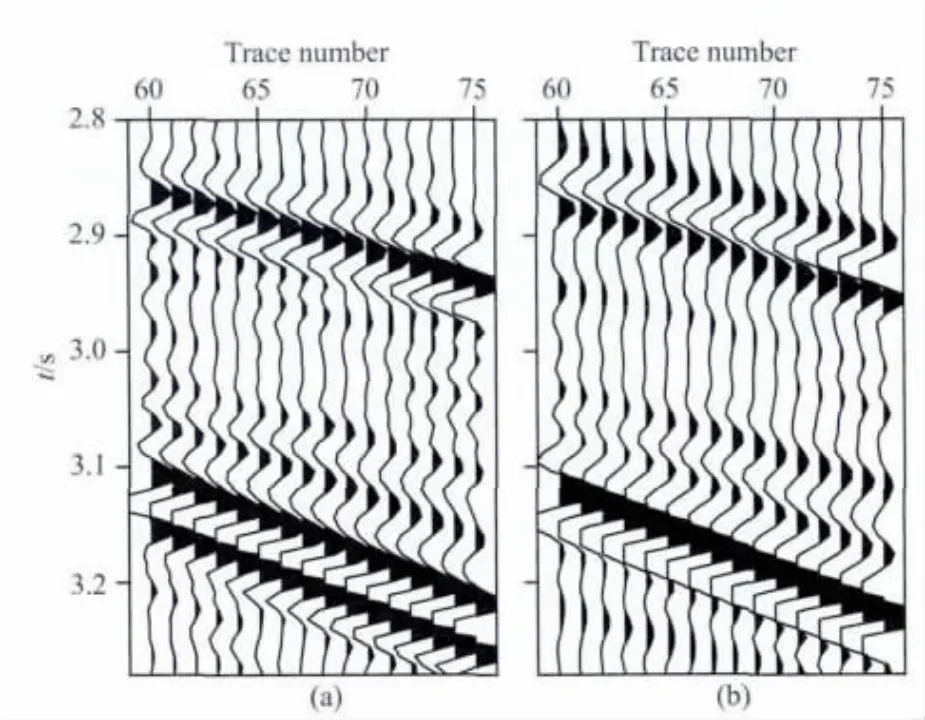
图9 SMAART 模型去除鬼波前后的炮集局部对比图（a）图8a中矩形区域的放大图；（b）图8b中矩形区域的放大图．Fig．9 Comparison between parts of original shot gather and deghosted shot gather of SMAART（a）is the zoom of the rectangle part in Fig．8aand（b）is the zoom of the rectangle part in Fig．8b

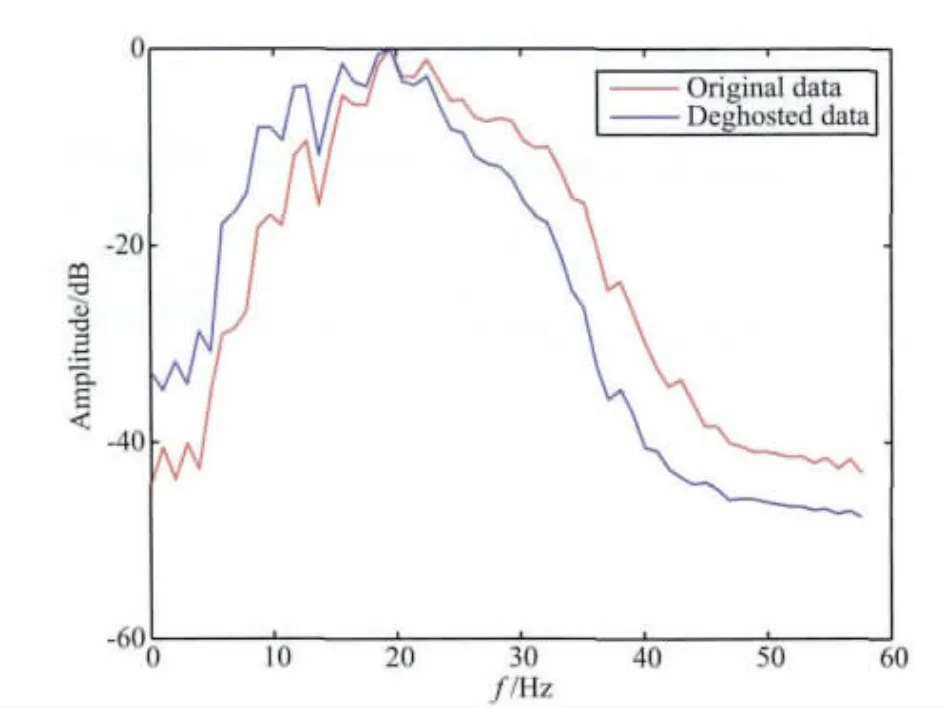
图10 SMAART 模型去除鬼波前后的炮集频谱对比图红色曲线为图9a对应的频谱，蓝色曲线为图9b对应的频谱．Fig．10 Comparison between amplitude spectrum of originalshot gather and deghosted shot gather of SMAART The amplitude spectrum of Fig．9a（red）and the amplitude spectrum of Fig．9b（blue）．

图11 鬼波压制前后的叠加剖面对比图（a）原始叠加剖面；（b）压制鬼波后的叠加剖面．Fig．11 Comparision between original stacked section and deghosted stacked section（a）Original stacked section；（b）Deghosted stacked section．

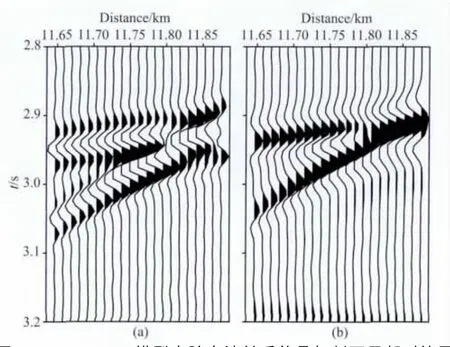
图12 SMAART 模型去除鬼波前后的叠加剖面局部对比图（a）图11a中矩形区域的放大图；（b）图11b中矩形区域的放大图．Fig．12 Comparison between original stacked section and deghosted stacked section of SMAART（a）is the zoom of the rectangle part in Fig．11a；（b）is the zoom of the rectangle part in Fig．11b．

4 结 论

开展了逆散射级数法鬼波压制理论与方法研究，详细论述了逆散射级数理论和逆散射级数法压制鬼波的原理，建立了鬼波压制处理流程，并对简单模型数据和复杂模型地震数据进行了处理试验和方法适应性分析，证明了方法的有效性．研究得到的具体认识如下：

（1）基于逆散射级数法的鬼波压制方法，不依赖于先验速度模型，适用于多维复杂介质，能在频率－波数－波数域较好的进行鬼波压制，恢复地震有效信息，有效保持一次波．

（2）基于逆散射级数鬼波压制方法能进行低信噪比地震数据处理，但对震源与检波点深度信息有一定依赖性．

（3）基于逆散射级数鬼波压制方法在三维地震数据上的应用原理与二维相似，研究方法可以推广到三维地震资料处理．

（4）相对于基于褶积模型的时间域鬼波压制方法和频率域鬼波压制方法，基于逆散射级数鬼波压制方法计算量稍大，设计并行运算将进一步提高方法的计算效率．

致 谢 在研究过程中得到了斯伦贝谢（中国）公司刘华锋博士的指导与帮助，在此表示感谢．

（References）

［1］ Lindsey J P．Elimination of seismic ghost reflections by means of a linear filter．Geophysics，1960，25（1）：130－140．

［2］ Schneider W A，Larner K L，Burg J P，et al．A new data processing technique for the elimination of ghost arrivals on reflection seismograms．Geophysics，1964，29（5）：783－805．

［3］ Ziolkowski A．Design of a marine seismic reflection profiling system using air guns as a sound source．Geophys，1971，23（5）：499－530．

［4］ Jovanovich D B，Sumner R D，Akins－Easterlin S L．Ghosting and marine signature deconvolution： A prerequisite for detailed seismic interpretation．Geophysics，1983，48（11）：1468－1485．

［5］ Robertsson J O A，Kragh E．Rough－sea deghosting using a single streamer and a pressure gradient approximation．Geophysics，2002，67（6）：2005－2011．

［6］ Ghosh S K．Deconvolving the ghost effect of the water surface in marine seismics．Geophysics，2000，65（6）：1831－1836．

［7］ Katibe A．The footsteps of the receiver ghost in the f－k domain．Geophysics，1999，64（5）：1618－1626．

［8］ Fang Y F．The method of eliminating marine seismic ghost reflections inf－kdomain．WorldGeology，1999，18（1）：75－77．

［9］ Weglein A B，Shaw S A，Matson K H，et al．New approaches to deghosting towed－streamer and ocean－bottom pressure measurements．72nd SEG abstract，2002：1016－1019．

［10］ Zhang J， Weglein A B．Extinction theorem deghosting method using towed streamer pressure data：Analysis of the receiver array effect on deghosting and subsequent free surface multiple removal． 75th Annual International Meeting，SEG，Expanded Abstracts，2005，24：2095－2098．

［11］ Mayhan J D，Terenghi P，Weglein A B，et al．Green′s theorem derived methods for preprocessing seismic data when the pressure P and its normal derivative are measured．SEG San Antonio 2011Annual Meeting，2011，2722－2726．

［12］ Weglein A B，Gasparotto F A，Carvalho P M，et al．An inverse－scattering series method for attenuating multiples in seismic reflection data．Geophysics，1997，62（6）：1975－1989．

［13］ Moses H E．Calculation of the scattering potential from reflection coefficients．PhysicalReview，1956，102（2）：559－567．

［14］ Prosser R T． Formal solutions of inverse scattering problems．JournalofMathematicalPhysics，1969，10（10）：1819－1822．

［15］ Razavy M．Determination of the wave velocity in an inhomogeneous medium from the reflection coefficient．JournaloftheAcousticalSocietyofAmerica，1975，58（5）：956－963．

［16］ Stolt R H，Jacobs B．Inversion of seismic data in a laterally heterogeneous medium．SEPRep．，1980，24：135－152．

［17］ Weglein A B，Boyse W E，Anderson J E．Obtaining theredimensional velocity information directly from reflection seismic data：an inverse scattering formalism．Geophysics，1981，46（8）：1116－1120．

［18］ Weglein A B，Gasparotto F A，Carvalho P M，et al．Inverse scattering series and seismic exploration．InverseProblems，2003，19（6）：R27－R83．

［19］ 金德刚．基于波动方程的层间多次波预测方法研究［博士论文］．北京：中国科学院地质与地球物理研究所，2008．

Jin D G．Internal multiples predication methods based on wave－equation ［Ph．D．thesis］（in Chinese）．Beijing：Institute of Geology and Geophysics，Chinese Academy of Sciences，2008．

［20］ 李翔，胡天跃．逆散射级数法去除自由表面多次波．地球物理学报，2009，52（6）：1633－1640．

Li X，Hu T Y．Surface－related multiple removal with inverse scattering series method．ChineseJ．Geophys．（in Chinese），2009，52（6）：1633－1640．

［21］ 刘华锋．逆散射级数法衰减海上多次波［博士论文］．北京：中国石油大学（北京），2011．

Liu H F．Marine multiple attenuation using inverse scattering series method［Ph．D．thesis］（in Chinese）．Beijing：China University of Petroleum（Beijing），2011．