行星会合指数变化与太阳绕太阳系质心运转的周期
刘复刚,王 建
1 南京师范大学地理科学学院,南京 210023
2 齐齐哈尔大学理学院地理系,齐齐哈尔 161006
1 引 言
研究表明,太阳活动具有11.1 年[1]、22 年[2-4]以及178.73年[5]的周期,从而导致地球气候与环境变化也具有类似的周期[6-7].关于太阳活动周期的形成机制,一般认为与行星会合引起的对太阳引力变化有关[8-10].因此讨论会合周期,对于深入理解太阳活动以及地球环境变化周期的形成机制,具有重要意义.但想得到两颗以上行星会合周期,目前还没有一个统一有效的方法.因此,建立一个标识行星会合的指数及其计算方法,就显得尤为重要.
以求算木星和土星的会合周期为例.这里所说的周期,如不特别说明,就是围绕太阳运转一周的历时.如地球绕日公转的真正周期是1 恒星年,T=365.256 日.已知木星和土星的周期分别为TJ=4332.587天和TS=10759.22 天(见表2).木星的角速度大于土星的角速度,木星总有追赶上土星的时候,即两者一定具有相同日心经度的时刻.从这一时刻开始,两者再次具有相同日心经度时,它们所转过的角度差为2π.设两者再次会合,且具有相同日心经度的时间间隔是T,并将木星和土星周期代入(1)式,

就木星和土星而言,两者的会合周期是19.8585年.将金星周期224.701 天(见表2)和木星周期代入(2)式,则得到金星和木星的会合周期为0.6489年(约237.0146天).但求算3颗或4颗行星会合周期就更困难.
应用求渐近分数的方法,通过求会合在一定角度(15°)范围内的木星、土星和海王星会合的准周期,则存在一个是土星和木星会合周期9倍的准周期,即为178.7268年.这和Jose(1965)[5]计算的太阳绕太阳系质量中心的角动量和太阳绕瞬时曲率中心的角动量时发现的178.77年周期是一致的.
2 求算木星同土星与海王星具有相同日心经度的会合周期
两颗行星可以从理论上求算出它们与太阳共面(具有相同的日心经度)的会合周期,虽然求算三颗行星精确的会合周期很难,但可以求出它们会合时,与太阳(圆心角顶点)形成的角度在一定的范围内.用这个角度来反映行星的会合程度是合理的.一般认为这个角度在40°之内就算会合了,为了凸显地外三颗大质量行星会合的紧密程度,把夹角小于或等于15°作为会合的标准.
通过SkyMapPro软件得知:在2993年12月4日8时0分0秒时,木星和土星的日心经度分别为327°14′51.6″和327°14′47.1″,两者相差0°0′4.1″.这时海王星的日心经度为328°27′59.2″,海王星与土星相差1°13′12.1″.就是说在公元2993年12月4日8时0分0秒时(2993.92629年),木星、土星和海王星三颗行星的日心经度近似相等.这也说明,在理论上三颗行星会合是可以给出较精确的会合周期.
根据文献[11],设经过t年后它们相聚在与日心成15°角的范围内,那么时间t一定是19.8585年的整数倍,即t=19.8585n(n为自然数).把土星和木星视为一颗行星(海王星周期164.7858 年或60189天,土星周期为29.4567年或10759.22天),把土星和海王星的周期数据代入(3)式,
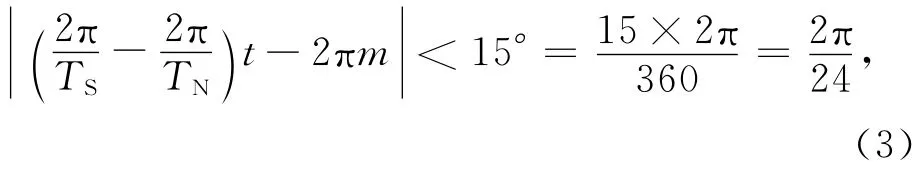
从而得

将(4)式变换为:

将t=19.8585n和土星、海王星周期代入(5)式,得:

其中m和n为自然数.由(6)式可知,由自然数n,m构成的有理数n/m是与35.8684/19.8585最接近,不妨设n/m=35.8684/19.8585,并将其转化成渐近分数,如(7)式,

(7)式中最明显的渐近分数,分别是:1/1,2/1,9/5,56/31.显然当m=1,n=1,2时,代入(6)式中都不满足要求.所以,当m=5,31,n分别对应m等于9,56时,三颗行星会合具有的最明显周期是178.7268年和1112.0760年.这时,木星、土星和海王星三颗行星都会合在15°范围内.因为此三颗大质量行星会合,一定是太阳绕太阳系质心角动量的极值状态(此时太阳距太阳系质心距离最远,太阳对应的太阳系质心绕转半径达到极大值).上述求算得到的三颗大质量行星会合周期178.7268 年与Jose(1965)计算得到的178.77年周期不但完全吻合,而且其所揭示的物理意义也是一样的.
以往学者都是从时间点上,推算行星会合与太阳活动的对应关系,进而得出两者间的可能联系.然而,这样得到的行星会合周期,只是时间点上的近似重复,并不能反映行星会合程度和相背离(行星的日心经度相差近180°)的变化过程和形态特征.而且,这种方法在寻找多个行星会合周期时几乎无法实现.
通过建立行星会合指数运动学方程的物理学方法,寻找行星会合指数达到极值状态的周期,进而发现行星系质心的运动轨迹和连续变化的形态特征.它与上述方法相比的最大优势在于,会合周期与时间是一一对应关系.运用这样的对应关系,就可以推之过去和预测未来太阳绕太阳系质心的运动特征.
3 行星绕日会合指数运动学方程的建立
如图1,以太阳为坐标原点(视太阳为不动点),以“不动平面”为行星系统的平均轨道平面[12](它是垂直于太阳系各天体的角动量的矢量和的平面,因为各行星轨道面与不变面的倾角都非常小,最大的是水星为6°17′,而木星、土星和海王星的倾角都不超过1°,因此,本文将各行星轨道平面视为在同一平面内是合理的)建立坐标系.不妨设三颗行星绕日公转的角速度分别为ω1、ω2和ω3,三颗行星所处的位置分别为P1、P2和P3,三颗行星位置的直角坐标分别为P1(r1cosα1,r1sinα1)、P2(r2cosα2,r2sinα2)和P3(r3cosα3,r3sinα3),其中r1、r2、r3分别为以各自质量为权重所得到的行星距太阳的加权平均半径.α1、α2、α3分别是r1、r2、r3与以横轴为基准轴所转过的角度,即为行星的日心经度(日心黄经).理论上,当三颗行星会合具有相同的日心经度时,三个半径向量的矢量和的模将达到最大值.为此,把行星绕日旋转轨道的向量半径矢量和的模,除以1个天文单位的距离长度,定义为行星会合指数(注:因为采用以各自质量为权重所得到的行星距太阳的加权平均半径的矢量和就是行星系统的质心).

图1 行星会合示意图Fig.1 The sketch map of planetary rendezvous
因为:

所以:
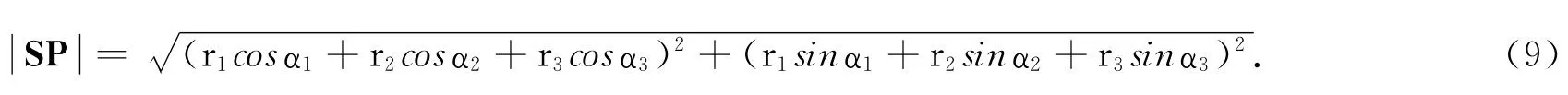
仿此,可以得到太阳系8大行星会合的一般运动学方程为:

其中,K,ri,φi,ωi分别为行星会合指数(K≥0)、以各自行星质量为权重的平均轨道半径、行星初始日心经度和平均角速度.当8大行星日心经度近似相等时,且位于太阳一侧,则会合指数K就指代行星系统处于会合的极大值状态;当木星和其它行星分别位于太阳的两侧,日心经度相差近180°时,则会合指数K就指代行星系统处于相背离的最大程度,即K的极小值更加接近0.这样就可以通过行星会合指数K的指代作用,绘出行星会合与相背离的极端状态的形态特征.
理论上,当土星、天王星和海王星与木星日心经度相差接近180°时,木星的矢量模与前三者的矢量模之差为ΔK=-0.1237AU,一般情况下,行星相背离达不到在日心经度上共面的极端情况.而根据会合指数运动学方程得到的图像看,K皆大于零.因此,设定K≥0是合理的.
4 八大行星2000年1月1日12时的日心经度
应用行星会合指数运动学方程,可以寻找行星会合与相背离的准周期.下面建立以纵坐标为行星会合指数K,横坐标以公元2000年为坐标原点向过去推算的时间坐标的行星会合与相背离图像.将表1中相应的数值代入(10)式行星会合指数运动学方程.
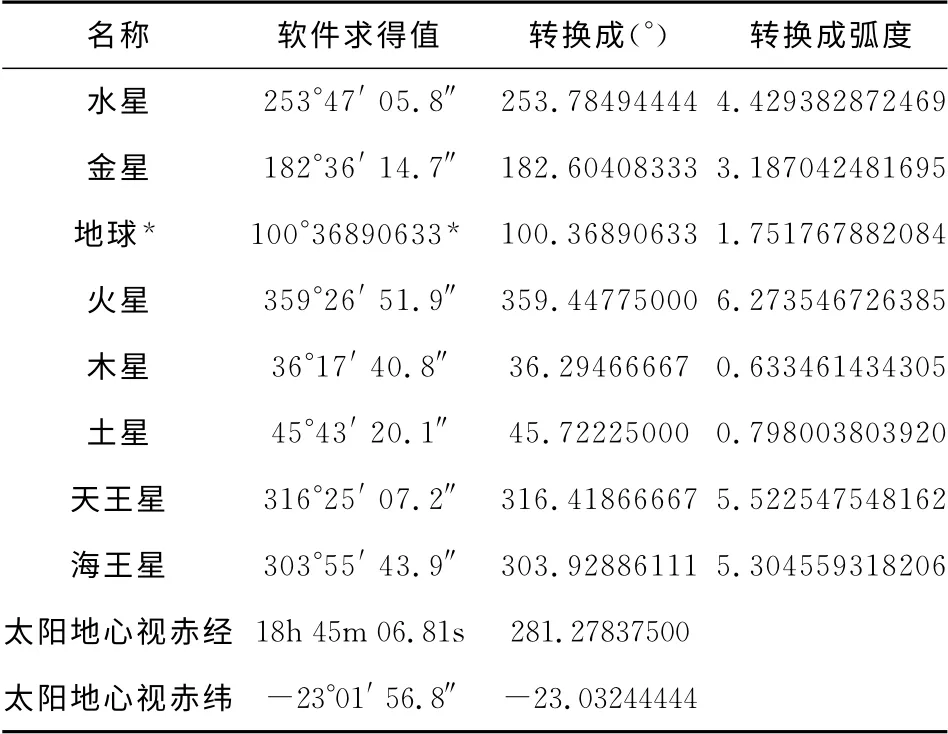
表1 八大行星2000年1月1日12时日心经度(φi)J2000历年(世界时)Table 1 The heliocentric longitude of the eight planets at 12o′clock on January 1st,2000
当只考虑木星与土星会合时,可以将木星和土星的绕日公转半径视为相等.设它们绕日公转半径都为1个单位,则会合指数Kmax=2,Kmin=0.从图2中得到,二者具有十分稳定的平均19.83年会合周期,这和计算得到的19.8585年周期近似相等.图3是以1天为单位时间步长,获得的金星和木星会合周期图像,它们有237.17天的会合周期.这和计算得到的237.0146天会合周期也近似相等.结果表明,我们建立的行星会合指数运动学方程是准确的.


5 行星绕日会合指数运动学方程的应用
太阳是太阳系的中心天体,其质量占整个太阳系总质量的99.865%,已经证实,行星绕日公转轨道是椭圆.因为在行星绕日公转时,太阳不是不动.就二体绕转天体运动而言,绕转天体和中心天体都绕它们的共同质心转动.戴文赛(1979)计算每个行星分别和太阳绕二者质心绕转角动量所采用的公式[12]是:

这是把太阳绕二者质心运动的轨迹视为椭圆,如果将整个太阳系作为考察和研究对象,那么在较短时间尺度上,由于受到非二体运动的摄动影响,太阳绕太阳系质心的轨迹就不是椭圆.图4是以两颗大质量行星木星和土星绕日运动为例,说明太阳绕太阳系质心运转的一般特征.当二者运转到日心经度相差近180°且位于太阳两侧状态时,木星(A)和太阳(S)则以二者的质心2 进行绕转运动,方向如粗空箭头所示;而土星(B)和太阳(S)则以二者的质心1进行绕转运动,方向如细实箭头所示.这时就出现了,太阳既绕2点运转又绕1点运转,且方向相反.实际上,这是不可能的.那么太阳只能绕A、B 两者与太阳所形成的公共质心运转,此时太阳只能选择一个方向.因此,在分析太阳绕整个太阳系质心运转时,必须首先找到太阳系行星系统的质心运动规律,并由此推出太阳绕太阳系质心运动的周期.因为,太阳系质心总是在太阳和行星系统质心的连线上[12].

图4 太阳绕太阳系质心运转的说明Fig.4 Simple diagram of the Sun moving around the mass center of the solar system
5.1 太阳系行星系统质心的确定
假定有n个质点,它们的质量分别是m1,m2,…,mn,位于P1,P2,…,Pn诸点,这些点对某一指定的参照点O的位矢分别是r1,r2,…,rn,则质心C(或叫质点组的质量中心)对定点O的位矢rc满足(12)式关系[16]:

式(12)是将各质点的质量乘以其位矢并求和,然后除以总质量,显然仍代表一个位矢.这个位矢末端(始端仍在O点)所确定的一点,定义为质点组的质心.根据(12)式,将太阳系各行星的平均绕转半径ˉri转换成位矢权重半径ri,见表2.从求算出的以各行星质量为权重的位矢半径ri看,除木星、土星、海王星和天王星外,其它行星的位矢权重半径都很小,距离太阳1AU 单位的地球位矢半径只有2.2377×10-3单位(含月球质量).因此,决定太阳系行星系统质心的主要是地外木星、土星、海王星和天王星四颗大质量行星的运行位置.

表2 行星轨道相关天文数据Table 2 The astronomical data about the planetary orbits
5.2 根据会合指数方程绘制行星系统质心绕日运动轨迹图像
将8大行星质量权重半径ri,2000年1月1日各行星日心经度(φi)和各行星的角速度值代入行星会合指数运动学方程,通过方程绘出了行星系统质心绕日运动轨迹图像,如图5.已知太阳平均半径RS=6.9599×108m.当行星会合处在太阳一侧,且具有相同的日心经度时,整个行星系统的质心距太阳中心的距离为RP=7.51 AU=7.51×1.496×1011m,设太阳距太阳系质心的距离为RC,八大行星会合时,行星系质心到太阳系质心的距离为RPRC,并有由质心定义有Mr⊙=mrP[12],从而得:

因为RC>RS,所以,在行星高度会合时,太阳系质心位于太阳本体之外.
设会合指数K=R1为太阳系质心进入太阳本体时的临界值,因为此时太阳系质心刚好到达太阳表面,所以RS=RC,由(13)式得:

K=R1=3.471临界值,如图5中的点实线所示.
根据图5可以得到,行星会合和相背离都具有平均19.8585(约20)年的周期.另外,每一个峰值和谷值都分别具有179~180年的行星会合和相背离周期,即由9个20年准周期集合而成的准180年会合周期(如图5上方标注的AB、BC、CD、DE 的179~180年周期).因为行星系统质心和太阳质心接近或重合时具有准20年周期,根据会合指数K=R1可推知,太阳系质心进入太阳本体也具有约20年的准周期,但在各周期中太阳质心接近太阳系质心的程度是不同的,就在180年间相背离的程度也体现出明显的周期性变化.图5中M 处(1850AD),向过去到N 处(1670AD)的180 年 间,有 约40 年、40 年、100年凸显的行星相背离特征,这样的特征在以太阳与太阳系质心最接近(即相背离程度最高)时为起点的180年周期中是按上述规律重复出现的.从图6和图7 中的1950—1951 年到1990—1991 年间,确实存在太阳质心和太阳系质心近似重合的约40年左右的周期,这也进一步证实图5 的可靠性.另外,在M、N 两点处,是行星达到最大相背离程度的时候,而分别距M、N 两点之前的约半个周期相位的A、B处,是行星达到最大会合程度的时候.就是说,在B—N 和A—M 时段,会合指数K在最小时段内,发生由最大到最小的变化.因此,这应该是太阳活动在短时期内起伏最大的时段.同时,这两个时段也是太阳绕太阳系质心运转的角动量发生由最大到最小转变的时段.在图5中,A、B 处的会合指数K十分接近会合指数最大值Kmax=7.51,而M、N处的会合指数K十分接近会合指数最小值Kmin=0(处于最大程度的相背离状态).如果将太阳视为不动点,179~180年准周期也是太阳系质心绕太阳的一个十分明显周期.

图5 行星系统质心绕日不动点运动轨迹图像纵坐标为行星会合指数K,原点为2000年,横坐标为过去距2000年的时间间隔.该图像特征亦为太阳绕太阳系质心运转的运动轨迹图像.原点仍为2000年,横坐标仍为过去距公元2000年的时间间隔,但其时间步长尺度为1.0987年;其纵坐标放大了746.153倍.太阳系质心绕太阳质心运转的运动轨迹图像同图5.Fig.5 The path of planetary system mass center around the fixed point of the SunVertical coordinate represents K,the origin represents the year of 2000,and the horizontal coordinate represents the time span from the past to the year of 2000AD.The image also describes the path of the Sun orbiting the mass centre of the solar system.The origin represents the year of 2000,and horizontal coordinate represents the time span to 2000,but the time unit was 1.0987-year.The vertical coordinate enlarged 746.153times.The image for the path of solar system mass center orbiting the Sun is similar to Fig.5.
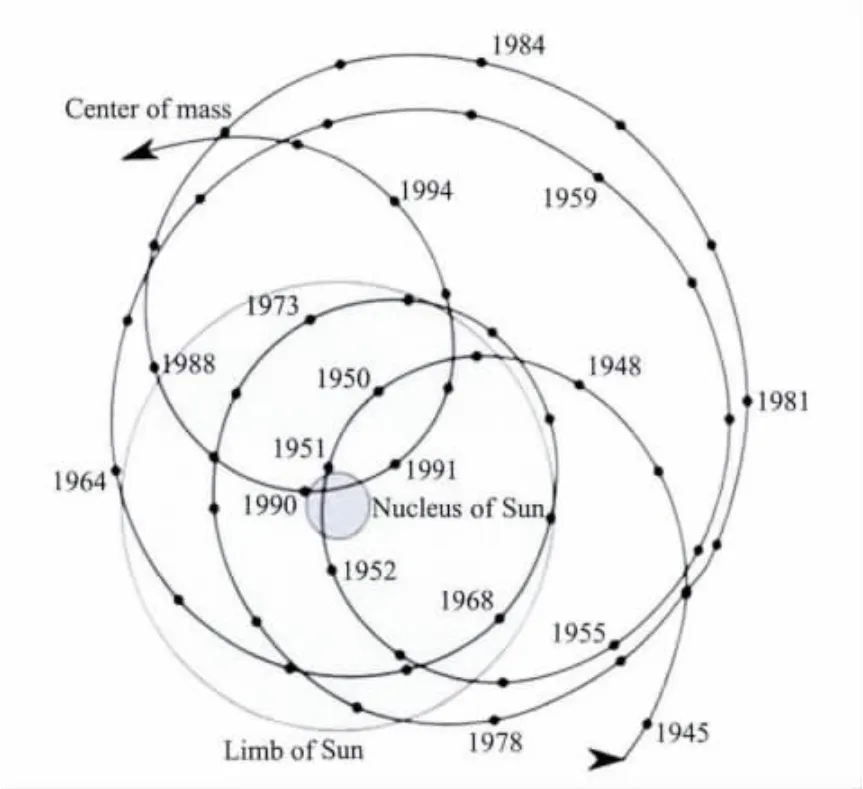
图6 太阳系质心相对于太阳的运动轨迹[17]Fig.6 Trajectory of the mass center of the solar system relative to the Sun[17]

图7 1940—2000年太阳中心相对于太阳系质心的运动轨迹r为春分点方向,虚线为1950年处太阳位置[18].Fig.7 Trajectory of the Sun center relative to the mass center of the solar systemris the direction of the vernal equinox.Dashed line is the position of the Sun in 1950[18].
因为行星会合指数最大值Kmax=7.51,而太阳系质心进入太阳本体时的行星会合指数临界值K=3.471,且小于Kmax的一半,从图5看出,K临界值与行星系质心绕太阳不动点轨迹相交各点,与峰值对应的平均宽度(时间)大于与谷值对应的平均宽度(时间).因此,在太阳绕太阳系质心运转的20年准周期中,平均而言,太阳系质心位于太阳本体之外的时间略长于位于太阳本体之内的时间.
这种运动特征更重要的物理意义在于:当太阳系质心与太阳质心十分接近或近似重合时(实际上就是行星系统质心和太阳质心与太阳系质心三者近似重合),此时太阳的轨道角动量近似为零,但它和行星系统共同绕太阳系质心同步运转运动没有停止,因此太阳绕太阳系质心运转和太阳自转运动是近似绕同一个质心进行,即相当太阳绕太阳系质心的运转运动叠加到太阳的自转运动之中.这时,此前太阳的绕转角动量绝大部分或全部转化为太阳自转角动量,这就必然导致太阳自转速度的增大.
5.3 求算太阳绕太阳系质心运转的恒星周期
太阳系行星的周期都是相对于遥远恒星绕日一周所需的历时.那么太阳系行星系统的质心绕日公转的周期(相对于遥远的恒星)是否可以求出?按照求各行星质量权重半径的方法,根据各行星的质量权重求得行星系统质心绕日旋转的加权平均周期(恒星周期),即

这里是行星系统质心相对于遥远恒星的绕日运转周期.
根据行星会合指数K得到的8大行星绕太阳不动点的平均会合周期为19.8585年,该周期正是太阳系中最大的两颗行星木星(★)和土星(☆)的会合周 期.在图8中1时刻,当S-C-★-P-☆与恒星()在一条直线上时,行星系质心处在以质量为权重获得的加权平均恒星周期ˉT的起点上,这是将整个行星系统质心看成由8大行星质量集聚到一起形成的一颗行星质心,所以该恒星周期和单独的行星绕转一样,P与C(或S)间的距离保持常量.
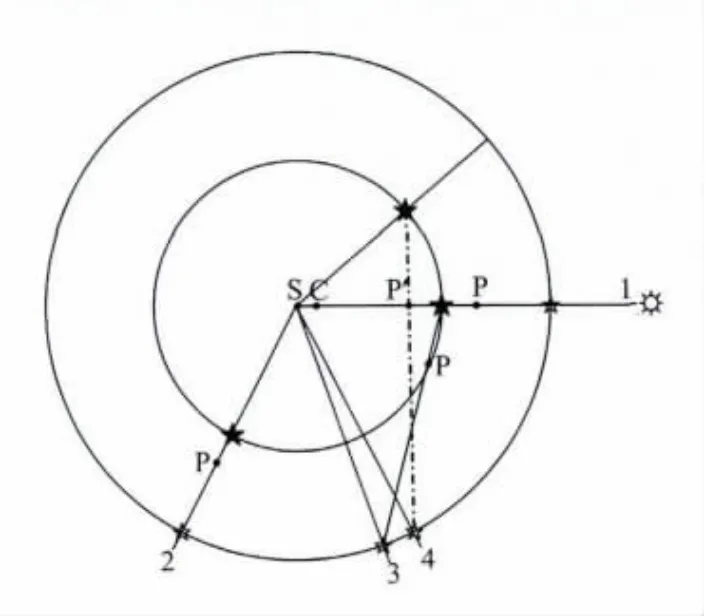
图8 行星系质心的恒星周期与会合周期示意图1、2、3、4为4个不同时刻P所处位置.Fig.8 The sketch map is about planetary system mass center moving of star cycle and planetary juncture′s cycle1,2,3,4is P the location for four different time.
根据木星(30.3490°/a)和土星(12.2208°/a)的绕转角速度,得到二者经过19.8585年再次会合的位置与起点相差117.32°(∠1S2).注意:这时木星和土星会合周期所确定的P位置距太阳系质心(或S不动点)间的距离是处于最大值.
会合周期不是恒星周期,当2时刻的P 再次回到1时刻初始位置时才经过一次完整的恒星周期.因木星和土星的角速度不同,当木星从2时刻位置再次运行到1 时刻位置时,土星与之相比落后70°(∠1S3).因为行星系统质心P 位于木星和土星的连线上,这时P位置处在3-★的连线上.在4时刻,当P再次回到1时刻初始位置的S-连线上时,则行星系质心P位于P′位置.这说明木星和土星绕太阳不动点运动的行星系质心的恒星周期不可能再次出现二者与太阳呈直线的会合周期,即不可能再次出现P-C(或S)间距离保持最大值的23.7799年周期.理论上,周期ˉT也是P绕C(或S)的运转周期,这时太阳不固定,行星系质心绕太阳动点运动距离是恒定的常量.这一距离应该与木、土两颗行星绕太阳不动点S 的会合周期状态下的行星系质心与太阳系质心距离具有极大值意义一样,因为它们都是行星系统质量高度集中在与太阳质心连线的方向.因此,理论上行星会合指数K指代的会合周期应该和行星系质心的恒星周期相同.因二者都是绕太阳系质心运动,之所以造成两周期的不同,是因为参照点太阳的动与不动所导致的.顾及到这两种情况都是太阳系质心处在行星系质心和太阳质心的连线上,故可求得P绕C的平均周期为:

因太阳绕太阳系质心的轨道运动周期与之相同,故也为21.8192年,约为22年.
由此得出结论:在太阳系中,太阳与整个行星系统质心是同步绕太阳系质心运转.所以太阳绕太阳系质心运转的平均周期也是21.8192年(约22年).
这时再称图5为“行星系统质心绕日运动轨迹图像”就不准确了,而应该称其为“行星系统质心绕日不动点运动轨迹图像”.因为真实的太阳绕太阳系质心运转的平均周期是21.8192年,而不是19.8585年.这样,作为太阳绕太阳系质心运转轨迹图像,图5的横坐标时间尺度的单位就应该进行改正,其改正系数为:

至此,就可以得到太阳绕太阳系质心运转的真实图像,如图5的注释.太阳绕太阳系质心运转的双世纪真实周期为(179~180)m≈196.6673~197.7660年,而不是179~180年.
图9是以时间尺度为1年获得的距2000(AD)年10000年的时间范围内,行星系质心绕太阳不动点的会合图像.其整体图像波动的峰值(极大值)和谷值(极小值)皆是由179 ~180年凸显的周期构成的具有约2300年(由峰值得到的)周期图像(或由谷值得到2325年的周期).根据上面的分析,该图像也可看成行星系质心和太阳绕太阳系质心运转的图像,只是需要改正.二者绕太阳系质心绕转的真正周期应该是1.0987×2300=2527a(通过会合指数运动学方程,可以获得行星的会合周期,如果要分析太阳绕太阳系质心的运转周期,就要乘上改正系数m).
“2300—2500年的周期旋回在冰芯钻孔、海洋钻孔、树轮、纹层沉积和湖面变化历史等记录中的气候替代性指标中都表现得很明显”[19].功率谱分析证实,黑子11年周期峰值的变化有188~212年的显著周期.由于这个周期的长度约为世纪周期长度的二倍,故得名.又因为这个周期和八大行星178.77年的会合周期接近,改正后的真实周期为196.67~197.77年(更接近双世纪),所以有人又称之为太阳活动的行星周期.由此可见,太阳活动尤其是太阳黑子活动的准周期同气候的变化规律与行星的驱动不无关系.
图10a中,正如上面所述,凸显的179~180年周 期 是 由 16—24—15—25—15—24—16—22—22—16年9个不严格等距的峰值(或谷值)周期集合而成.当把单位时间步长定为1天时(图10b),通过图10b和图10a的对比可以确定,当时间步长尺度变小时,行星系质心绕太阳不动点的会合周期所呈现的179~180年的周期(Suess-cycle)和约2300年的哈尔斯塔周期(Hallstatt-cycle)是稳定的.因此,通过改正系数m修正后的太阳绕太阳系质心运转的Suess-cycle和Hallstatt-cycle亦将十分稳定.
行星系统会合与相背离的极值状态分别与太阳活动的奇数周和偶数周对应.通过观测得知太阳活动的偶数周和奇数周的磁场极性是相反的,因此,行星会合指数K的极大值和极小值也具有指代太阳黑子磁场极性的作用.见图11所示.

图11 1600AD—2000AD 太阳绕太阳系质心运动轨迹与太阳黑子数的对应行星会合指数K 图像为乘以改正系数1.0987后的图像,(b)引自文献[20].Fig.11 The corresponding relationship between trajectory of the Sun orbitingthe mass center of the solar system and the sunspot number


6 结 论
(1)创建了行星会合指数运动学方程,通过定义的行星会合指数可以指代行星会合与相背离的程度.K愈接近7.5说明会合的程度越高;K愈接近0说明相背离的程度越高.进而发现行星系质心的运动轨迹、形态变化特征和会合周期.
(2)因为ri权重半径的矢量和就代表行星系统的质心位置,所以K值的大小就代表行星系统质心距离太阳(或太阳系质心)的远近.通过图像分析发现,太阳系质心绕太阳的转动有近半程时间是处于太阳本体之内.
(3)通过图5获得的行星系质心绕太阳不动点的周期与木星和土星的会合周期相同(因为两者的质量和占所有行星和卫星的质量总和的92.5%[12]),但它不是太阳绕太阳系质心运转的真正周期,通过分析求证获得了太阳绕太阳系质心运转的恒星周期是21.8192年(约22 年).通过会合指数运动学方程,可以获得行星的会合周期,但如果要分析太阳绕太阳系质心的运转周期,要乘上改正系数m.
(4)太阳由9个22年的基本磁周期合成了197年(约200年)的双世纪周期(Suess-cycle),又由约13个双世纪周期合成了2527 年(约2500~2561年)的哈尔斯塔(Hallstatt-cycle)长周期.正因为太阳绕太阳系质心运转具有稳定的22年准周期,从而造成太阳黑子具有22年磁周期的变化规律.
致 谢 十分感谢评审专家的精心审阅和提出的宝贵修改意见!
(References)
[1] 中国大百科全书编辑委员会<天文学>编辑委员会.中国大百科全书:天文学.北京,上海:中国大百科全书出版社,1980:352.
Encyclopedia of China:Astronomy (in Chinese).Beijing,Shanghai:Encyclopedia of China Publishing House,1980:352.
[2] Hale G E.On the probable existence of a magnetic field in Sun-spots.AstrophysicalJournal,1908,28:315-343.
[3] Parker E N.Hydromagnetic dynamo models.Astrophysical Journal,1955,122:293-314.
[4] Pablo D M,Daniel O G,Gabriel B M.Simple model of a stochastically excited solar dynamo.SolarPhysics,2001,201(2):203-223.
[5] Jose P D.Sun′s motion and sunspots.TheAstronomical Journal,1965,70(3):193-200.
[6] Stuwier M,Quay P D.Changes in atmospheric carbon-14 attributed to a variable sun.Science,1980,207(4426):11-19.
[7] 曲维政,邓声贵,黄菲等.太阳磁场磁性指数异常变化对南北半球中纬度气候的影响.地球物理学报,2004,47(3):398-405.
Qu W Z,Deng S G,Huang F,et al.Influence of magnetic index abnormal change in the solar magnetic field on climate at the middle latitudes of North Hemisphere.ChineseJ.Geophys.(in Chinese),2004,47(3):398-405.
[8] 杨志根.大行星运动对太阳黑子活动的可能影响.天体物理学报,1991,11(4):370-377.
Yang Z G.The possible influence of the orbital motion of the major planets on sunspot activities.ActaAstrophysicaSinica(in Chinese),1991,11(4):370-377.
[9] 杨志根,赵铭.太阳极性黑子相对数主周期的成因探讨.天文学报,1988,29(3):297-304.
Yang Z G,Zhao M.An investigation for the cause of formation of the major period of the relative sunspot numbers with bipolarity.ActaAstronomicaSinica(in Chinese),1988,29(3):297-304.
[10] 陈协珍.行星摄动力对太阳活动的调制.天体物理学报,1996,16(2):207-212.
Chen X Z. Solar activity modulation by planetary perturbations.ActaAstrophysicaSinica(in Chinese),1996,16(2):207-212.
[11] 华罗庚.从祖冲之的圆周率谈起.北京市数学会编.北京:人民教育出版社,1964.
Hua L G.Speak of Pi from Zu Chongzhi(in Chinese).Beijing:People′s Education Press,1964.
[12] 戴文赛.太阳系演化学(上册).上海:上海科学技术出版社,1979:12,22-23.
Dai W S.The Development of Solar System (Rudin)(in Chinese). Shanghai: Shanghai Scientific & Technical Publishers,1979:12,22-23.
[13] 朱光华,冯克嘉,彭望琭.普通天文学(地学用).北京:北京师范大学出版社,1990:17-24.
Zhu G H,Feng K J,Peng W L.Normal Astronomy(for Geography)(in Chinese).Beijing:Beijing Normal University Publishing Group,1990:17-24.
[14] 四川矿业学院数学教研组.数学手册(增订本).北京:煤炭工业出版社,1977:61.
The Mathematic Teaching and Research Group of School of Mining and Technology of Sichuan.Handbook of Mathematics(Revised and Enlarged)(in Chinese).Beijing:China Coal Industry Publishing House,1977:61.
[15] 刘南.地球概论.北京:高等教育出版社,1987:91.
Liu N.Introduction of Earth(in Chinese).Beijing:Higher Education Press,1987:91.
[16] 周衍柏.理论力学教程(第二版).北京:高等教育出版社,1986:112-114.
Zhou Y B.The Course of Theoretical Mechanics(Second Edition)(in Chinese).Beijing:Higher Education Press,1986:112-114.
[17] http:∥upload.wikimedia.org/wikipedia/commons/c/c7/Sunspot-number.png“Motion of the barycenter of the Solar System relative to the Sun”.
[18] 任振球.全球变化.北京:科学出版社,1990:23.
Ren Z Q.Globle Change (in Chinese).Beijing:Science Press,1990:23.
[19] Lowe J J,Walker M J C.第四纪环境演变.沈吉,于革,吴敬禄等译.北京:科学出版社,2010:408-409.
Lowe J J, Walker M J C.Reconstructing Quaternary Environments(in Chinese).Shen J,Yu G,Wu J L Trans.Beijing:Science Press,2010:408-409.
[20] http:∥en.wikipedia.org/wiki/Sun_spot_cycle“400 year history of sunspot numbers.”.

