六足机器人斜坡步态的设计
李栓柱,钟建锋,程 品,罗 欣
(华中科技大学数字制造装备与技术国家重点实验室,湖北 武汉 430074)
0 引言
六足机器人具有多足步行机器人的良好地面适应能力和步行灵活性的特点,同时能够承载一定的有效载荷,因而在高原山地大倾角斜坡环境下承担物资运输任务具有突出优势。但是为了避免机身与山地崎岖地形发生碰撞,因而机身重心离地面高,并且斜坡环境导致支撑腿脚力分配不均,这对于机器人在大倾角斜坡环境下工作时的稳定性极其不利。如何通过步态规划来提高多足机器人的稳定性是机器人研究的重要内容。Weingarten研究了六足机器人的自适应步态[1],以RHex六足机器人为代表,该机器人能够在沼泽、楼梯等环境下行走,有良好的表现;但其体积较小、易倾翻,并不能安全平稳地在山地斜坡环境下行走。G¨orner的 The DLRCrawler采用自由步态结合腿部柔顺控制方案[2],其体积小、地形适应性好且不易倾翻,但不具有有效的负载能力。Wettergreen对Dante II型六足机器人做了基于行为控制的自由步态的研究[3],该型机器人能够安全有效地在水平非结构地形下行走,且具有一定的负载能力;但其仍然在大倾角斜坡环境下仍然存在局限性。
将分析六足机器人在大倾角斜坡地形下与水平地面行走情况的不同之处,针对斜坡地形设计出具有高稳定裕度的斜坡步态以确保机器人行走过程中的稳定型、负载安全性,并对该步态进行稳定性分析。
1 六足步行机器人的结构及稳定裕度定义
1.1 六足步行机器人的结构
针对机器人工作在斜坡地形的情况,采用典型的六足机器人结构,其机身呈长方形结构,如图1所示。机身长度n=4m,宽度m=2.5m,机器人机身重量M=3t,其工作环境的斜坡倾角θp=35°。
如图1中所示,∑O为地面固定坐标系,∑C为机身固定坐标系,原点与机身几何中心重合,XOY平面与机身平行,Y轴指向前进方向,Z轴垂直于机身;机器人运动过程中,以地面固定坐标系∑O为参考点,∑C原点的坐标描述了整个机器人在环境中的位置,∑C的X轴、Y轴及Z轴方向向量表征机器人的姿态信息。

图1 六足机器人整机机械结构
腿部采用开链式杆结构,如图2所示,髋关节长度li1=300mm,小腿长度li2=900mm,大腿长度li3=900mm。为了保证单腿有足够的自由度,单腿具有3个独立驱动关节,每个关节均采用液压缸驱动,在保证位置伺服的同时提供较大关节力矩。∑Bi为机身髋关节坐标系,坐标系原点与机身髋关节几何中心重合,X轴,Y轴,Z轴方向与∑C的X轴,Y轴,Z轴方向相同,θi1,θi2,θi3为各个关节角度。

图2 六足机器人单腿机械结构
1.2 六足步行机器人的SSM稳定裕度的定义
SSM(static stability margin)[4]稳定判据是指在机器人的运动过程中,如果机器人的重心CG(center of gravity)投影点始终落在支撑多边形在水平面的投影范围内,则认为机器人是稳定;CG投影点距离投影支撑多边形各边的最小距离为SSM稳定裕度。
机器人在上坡行走过程中受力,如图3所示,点P为机器人重心,将P投影点P′到投影支撑多边形(a1,a2,…,a6组成)所在平面内,其中最小值即为其SSM稳定裕度是:其中,i,j=1,2,…,6。


图3 机器人受力状况
由于机器人工作在斜坡环境中,平行于斜坡平面的力分量较大,因而在平行于斜坡平面的力必须满足摩擦约束[5],表达式如下:

其中,μ为足地接触摩擦系数。
2 斜坡步态的设计
分析机器人斜坡行走步态,主要从髋关节初始角度配置、机身重心高度和迈腿顺序3个方面进行斜坡步态的设计,以满足高稳定裕度的要求。
2.1 各腿髋关节的初始角度配置
足式机器人中支撑腿相对于机身的姿态的布置既要考虑工作空间限制,又要考虑到机器人的稳定性。特别是工作环境为斜坡地形,稳定性是首要考虑的指标。在上坡过程中,机器人的重心投影点在Y向会向A3,A4连线靠近,如图4所示,与机器人在水平地形环境下行走时的重心投影点的分布不同,因而斜坡环境下工作的机器人支撑腿的立足点相对于机身的Y向位置是提高其工作时稳定性的重要因素,文中机器人立足端Y向位置取决于髋关节的角度,所以通过改变髋关节的初始角度配置能够提高机器人的稳定裕度。

图4 机器人斜坡环境下腿部姿态布置俯视
受机械结构约束,各腿髋关节工作空间为:θ11,θ61∈(-30°,90°);θ21,θ51∈(-60°,60°);θ31,θ41∈(-30°,90°),如图5所示。λ1,λ2,λ3为六步态行走过程中,可能出现的稳定裕度最小的3种情况。CG距离各边的最近距离λ1随θ21,θ61的变化趋势,λ2随θ21,θ41的变化趋势,λ3随θ41,θ61的变化趋势如图5所示。由图5可以看出,随着θ21的变化,λ1,λ2的变化呈相反的趋势,λ3保持在一个较大的范围内。

图5 λ1,λ2,λ3 随θ21,θ41,θ61变化的趋势
文中机器人参数、结构如1.1节所述,该情形下兼顾λ1,λ2,λ3同时在一个值较大的范围内 ,最终取得初始角θ110=θ610=10°;θ210=θ510=30°;θ310=θ410=45°。
2.2 机器人重心高度的设计
机器人在斜坡环境下工作时,如图3所示,重心投影会偏离各支撑腿所构成的支撑多边形中心,距离大小为L,L与H的关系为:

为保证机器人不与地面发生碰撞,同时受机器人的工作空间约束,取800mm<H<1 600mm。经计算,随着机身高度H的增大,λ1有增大的趋势,λ2有减小的趋势,λ3在小范围内减小。机身重心高度是影响稳定裕度的重要因素,因而设计步态时在保证机身未与地面发生碰撞的条件下,应尽可能的降低机器人重心高度,以获得较大的稳定裕度。本文中为了兼顾λ1,λ2,机器人重心高度取H=1 000 mm。
2.3 斜坡步态的机身和腿部运动顺序
为保证机器人在斜坡上行走具有较大稳定裕度,因而机器人在机身移动过程中六条腿同时支撑以保证稳定性;机身完成移动后,支撑腿按特定的顺序交替地摆动、支撑。针对六足机器人在大倾角的斜坡行走的情况,在上坡过程中CG投影点偏离支撑多边形中心,靠近A3,A4所确定的边界,在Leg4(Leg3)摆动过程中A1,A2,A3(A4),A5,A6构成的支撑多边形缩小,重心投影可能偏离出多边形,导致机器人失稳。同时在斜坡环境下,机器人腿部支撑力的分配不均,其中以Leg3,Leg4受力最大为主要支撑腿,Leg2,Leg5次之,Leg1,Leg6最小。随着机器人重心的前移,Leg1,Leg6,Leg2,Leg5的支撑力增大,Leg3,Leg4支撑力减小,此时Leg2,Leg5成为主要支撑腿。在一个步态周期内Leg2,Leg5和Leg3,Leg4交替作为重要支撑腿。在设计迈腿顺序时,应满足在一个步态周期的某段时间内,若某腿为重要支撑腿,则其不摆动的原则。如图6所示,当机器人完成重心前移时,图中实线代表该步态周期内Leg3,Leg4在时间上先于Leg2,Leg5迈步,此时的最小稳定裕度为λA;点划线代表该步态周期内Leg2,Leg5在时间上先于Leg3,Leg4迈步,此时的最小稳定裕度为λB,经计算仿真,在所述的条件下,λA>λB,最终确定斜坡步态的机身及腿部的动作顺序 为 Leg1—Leg6—Body—Leg4—Leg3—Leg2—Leg5。

图6 机器人机身与各腿运动顺序表
3 仿真实验及结果分析
为证明斜坡步态在斜坡环境下能够保证机器人稳定行走,因而在35°斜坡情况下对文中所述六足机器人斜坡步态的稳定裕度的仿真分析,分4个实验进行。仿真实验中,机器人的结构参数以及斜坡环境参数如1.1节所述。对规划的步态控制算法进行仿真实验,得到图形仿真结果,根据仿真结果验证步态的稳定性。
仿真实验是基于ADAMS/C联合仿真技术进行,ADAMS建立机器人动力学模型,Simulink构造控制算法。对于Matlab控制系统而言,其输出对应于ADAMS构造的机器人模型的输入;二者有机结合构成闭环控制系统的仿真设计。
3.1 髋关节的初始角度配置对稳定裕度影响的仿真与分析
实验1采用髋关节初始角度为0°的平行对称布置,实验2采用2.1节优化后的结果θ110=θ610=10°;θ210=θ510=30°;θ310=θ410=45°的布置,其他实验条件二者均相同。仿真实验得到的稳定裕度曲线如图7所示,横轴为时间,纵轴为机器人稳定裕度。髋关节初始角度为0°的初始布置中,整个步态周期内出现了稳定裕度为0的时刻,这意味着此时机器人失稳;优化髋关节初始角度布置后使得整个步态周期中的稳定裕度,统计结果如表1所示。

图7 实验1~4稳定裕度曲线
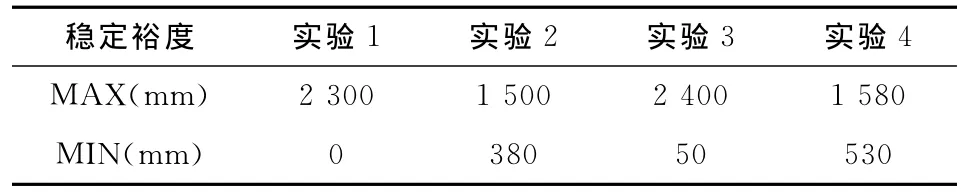
表1 各实验中稳定裕度最值统计表
步态稳定裕度的最大值有所减小,但是最小值却明显增大,能够保证整个步态周期内机器人稳定行走,证明了髋关节初始角度优化后能够明显的提高机器人在斜坡行走时的稳定裕度。
3.2 迈腿顺序对稳定裕度影响的仿真与分析
实验1、实验3均采用髋关节初始角度为0°的配置,不同之处在于实验1采用的迈腿顺序为Leg1—Leg6—Body—Leg5—Leg2—Leg3—Leg4,而实验3采用的迈腿顺序如3.2节分析结果为Leg1—Leg6—Body—Leg4—Leg3—Leg2—Leg5。实验1、实验3得到的机器人行走稳定裕度曲线,如图7所示。纵轴为稳定裕度值,图中改进迈腿顺序的实验3中最小稳定裕度尽管很小但未出现失稳情况,整个步态周期内机器人稳定行走,说明了改进后的迈腿顺序对提升机器人稳定裕度的有效性。
实验2、实验4均采用的髋关节初始角度如2.1节分析结果,θ110=θ610=10°;θ210=θ510=30°,θ310=θ410=45°的布置,不同之处在于实验2采用的迈腿顺序为Leg1—Leg6—Body—Leg5—Leg2—Leg3—Leg4,而实验4采用的迈腿顺序如2.3节分析结果为 Leg1—Leg6—Body—Leg4—Leg3—Leg2—Leg5。实验2、实验4得到的机器人行走稳定裕度曲线,如图7所示,说明改进迈腿顺序对稳定性有着一定的效果。比较图7看出,稳定裕度最小值均发生在Leg4,Leg3摆动的时间段内,由于上坡过程中Leg4,Leg3为主要支撑腿,CG投影点靠近支撑多边形后半部分,故而在二者摆动时间段内稳定裕度较小;分别比较实验1和实验2、实验3和实验4,后者的稳定裕度显著大于前者,说明髋关节初始角度配置对稳定裕度的影响大于迈腿顺序的优化结果。
3.3 重心高度对稳定裕度影响的仿真与分析
为了分析机身重心高度对机器人在斜坡行走过程中SSM稳定裕度的影响,分5次仿真实验进行,5组实验机身高度分别为H1=800mm,H2=1 000 mm,H3=1 200mm,H4=1 400mm,H5=1 600 mm,所得到的稳定裕度曲线如图8所示,纵轴为稳定裕度值,横轴为机身重心高度值。由图中可以得出,随着机身重心高度的增大,在机器人上坡行走构成中的最小稳定裕度减小,说明降低机身重心的高度有利于提高机器人在斜坡上行走时的稳定裕度,在上坡行走过程中应尽量降低重心高度。

图8 稳定裕度-机身重心高度关系曲线
4 结束语
对六足步行机器人斜坡行走过程中对平稳性以及安全性要求进行了分析。通过优化髋关节初始角度、机身重心高度以及迈腿顺序的优化完成斜坡步态的设计,以此提高机器人斜坡行走的稳定裕度,通过仿真实现机器人上坡行走,证明了步态的有效性,为下一步进行实地实验奠定了基础。
[1]David Wettergreen,Chunck Thorpe.Developping planning and reactive control for a hexpod roebot[A].in Int Conf,Rob.and Aut,IEEE[C].1996.
[2]Weingarten J D,Lopes G A D,Buehler M,Groff R E,Koditschek D E.Automated gait adaptation for legged robots[A].in Submitted to 2004IEEE International Conference on Robotics and Automation[C].2003.
[3]G¨orner M,Wimb¨ock T.The DLR-Crawler:A Testbed for actively compliant hexapod walking based on the fingers of DLR-Hand II[A].Proceedings of the 2008IEEE/FSJ International Conference on International Robots and Systems[C].Nice,France.
[4]夏旭峰,葛文杰.仿生机器人运动稳定性的研究进展[J].液压与机床,2007,35(2):229-234.
[5]陈学东,孙 翊,贾文川.多足步行机器人运动规划与控制[M].武汉:华中科技大学出版社,2006.

