基于SIMPACK的轨道车辆动态性能仿真分析

黄安宁，易智民，张安全

（重庆旗能电铝有限公司工程技术一部，重庆 綦江 401420）

0 引言

在铁路事业高速发展过程中，轨道车辆的安全性也就凸显得更加重要。因此对于轨道车辆的部件以及整车的动力学性能分析的重要性就显得格外突出，并且具有重要的现实意义。某型轨道车辆是我国自主研制的大型铁路养路机械，它的整体动力学性能直接影响到其行驶的安全性和养护铁道线路的质量，因此，有必要对其进行全面的动态性能研究。

1 轨道车辆动力学模型建立

在SIMPACK软件中，多体系统的拓扑图形建立的好坏直接和模型建立的正确与否相关，并且关系到所建模型的复杂程度以及规模的大小，也涉及到最终的动力学方程的求解时间和计算效率[1]。某型轨道车辆系统拓扑关系如图1所示[2]。在SIMPACK软件中建立的整车模型如图2所示。某型轨道车辆是具有二系悬挂弹簧的一个多自由度的振动系统，主要由轮对、转向架和车体这3大部件组成。多体系统分析中，拓扑结构是系统建模的一个十分关键的前期工作。

图1 轨道车辆系统拓扑关系

图2 轨道车辆整车模型

2 轨道车辆动力学仿真

在轨道车辆的动态性能指标中，车辆的线性临界速度和非线性临界速度可以判断车辆安全行驶的最高速度；而车辆的脱轨系数和倾覆系数则可以更进一步确定该车辆行驶的安全性能；而车辆行驶的平稳性指标则是考察车辆乘坐舒适性。

2.1 线性临界速度分析

采用SIMPACK软件进行仿真时，设置轨道车辆的运行速度区间为150～300km／h，速度增量为20km／h。求解得到的某型轨道车辆根轨迹图如图3所示。根轨迹曲线图是在不同运行速度下轨道车辆运动微分方程一系列特征值的集合，其横坐标为无量纲的阻尼比系数（特征根实部），纵坐标为相应模态的振动频率（特征根虚部）[3]。图3中所示的每一条根轨迹曲线都由11个“＋”符号组成。随着轨道车辆速度的变大，“＋”符号也变大 。“＋”符号随速度变化较大的是轮对和转向架轨迹的蛇行以及构架的横向振动 ，而不随轨道车辆运行速度变化或变化不大的振动模态就是系统中各刚体的振动模态，对应的频率就是它们的固有振动频率[3-6]。根据图3所示的根轨迹图，有2个“＋”符号位于图形的实部，可以判定该轨道车辆的线性临界速度高于250 km／h，但低于300km／h。

图3 轨道车辆根轨迹

2.2 非线性临界速度分析

在仿真轨道上设置一段长度为50m的美国5级轨道谱做为其不平顺性的激扰，使仿真车辆以不同的速度在此轨道上通过。根据轮对的横线位移曲线是否发生了发散现象，判断该型号车辆的稳定性和非线性临界速度[7-8]。选取第3轮对的横向振动位移作为车辆稳定的判断依据[9]，经过SIMPACK运动仿真后的结果如图4所示，横坐标为轨道车辆的运行时间，纵坐标为其轮对的横向振动位移。

图4 轨道车辆非线性临界速度判断

当轨道车辆速度为232km／h时，随着时间的推延轮对的位移是收敛的，这时轨道车辆是稳定的。而当轨道车辆的速度达到233km／h时，约1.8s后，轮对的横向位移并不随着时间的推延而发生衰减，而是在中心位置来回的振荡，表明轨道车辆在运行过程中，系统在横向方向发生了稳态的强迫振动，这时轨道车辆系统是不稳定的。在图4中显示的0～1s区间内，轨道车辆以两种速度运行时，在轮对的横向方向均发生了一个较大的偏移，是由于车辆行驶在一段无激励轨道上后突然被施于轨道激励的瞬时变化情况。由图4可判定该型号的轨道车辆的非线性临界速度为232km／h。

2.3 轨道车辆曲线通过能力分析

轨道车辆在通过曲线轨道时，如果速度过快，很可能发生脱轨事故，因此，对其曲线通过能力的分析是很有必要的。依照参考文献[10]设置仿真轨道的曲线，轨道曲线由直线、进出的缓和曲线及圆曲线组成。考虑来自轨道的不平顺性，以美国5级线路轨道谱作为线路的随机激扰。轨道车辆的曲线通过性能如表1所示。

表1 轨道车辆曲线通过性能表

由表1可知，该型号的轨道车辆在以一设定的速度通过设置好的曲线线路后，获得的轨道车辆的轮轨横向力最大值为14.77kN，轮轨的垂向力最大值为66.43kN，轮轴横向力最大值为22.7kN，脱轨系数最大为0.25，倾覆系数的最大值为0.39，均小于GB5599—1985[11]中所规定的值，并且有较大的安全余量。上述的分析表明，该型号的轨道车辆以速度140km／h运行在正常的Ⅰ级以及Ⅱ级轨道线路时，车辆的行驶安全还是有较大保障的。

2.4 轨道车辆平稳性分析

由于轨道不平顺的激励，轨道车辆在行驶过程中将产生振动，振动的强度和振动持续时间有可能会给乘坐人员带来不适的感觉。因此，车辆运行的平稳性和舒适性也越来越受到人们的重视。在本论文中，轨道车辆分别以60km／h，80km／h，100km／h，120km／h，140km／h的速度运行通过以美国5级线路轨道谱为激励的直线轨道上，获取该轨道车辆的各加速度曲线图和加速度频响，运行平稳性指标如表2～3所示。

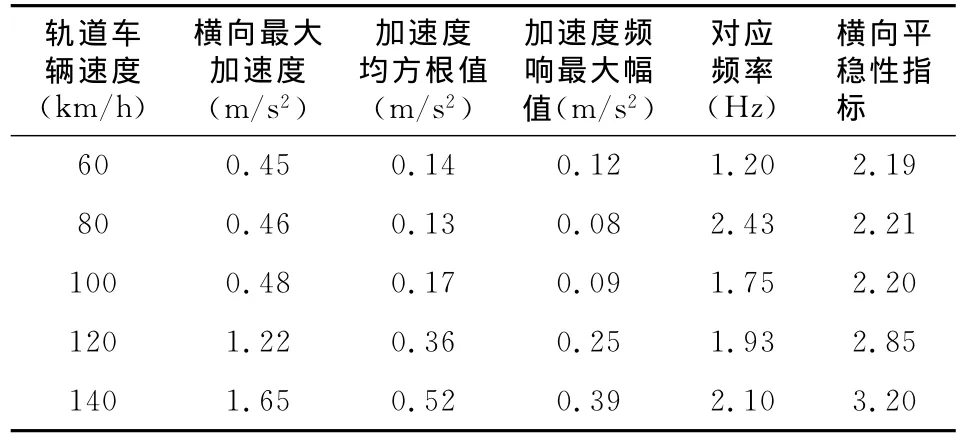
表2 轨道车辆中心横向振动加速度及平稳性指标

表3 轨道车辆中心垂向振动加速度及平稳性指标

从表2和表3中可以获知，该车辆以100km／h轨道车辆中心横向加速度的最大值为0.48m／s2；垂向加速度的最大值为0.94m／s2；横向平稳性指标最大值为2.20。其中最大垂向平稳性指标为2.06，均小于2.5。对照参考文献[11]中规定的平稳性指标，可以评定该型号的轨道车辆在速度为100 km／h行驶时，其平稳性等级为1级。说明该型号的轨道车辆的行驶速度为100m／s2时，具有良好的平稳性，舒适程度较高。而速度达到120km／h时，其横向平稳性指标最大值为2.85，平稳等级属于合格；而速度达到140km／h时，其横向平稳性指标最大值达到了3.2，平稳等级属于不合格。依照平稳性指标的评定等级，该型号的轨道车辆运行速度应低于120km／h。

3 轨道车辆车体的刚柔耦合分析

在ANSYS中建立车体和构架有限元模型，并进行模态分析，获得车体的前三十阶模态。在有限元软件中对有限元模型进行缩减后，然后利用SIMPACK的FEMBS接口经过FRM（frequency response mode）分析后生成.SID文件，最后将该文件导入SIMPACK软件中的动力学模型中，生成了具有柔性车体的整体动力学模型[2，12]。

轨道车辆的速度设置为100km／h，以美国5级线路谱作为轨道仿真的激励，经过积分运算后，可知轨道车辆运行时的柔性车体变形情况如图5所示。

图5 柔性车体变形情况

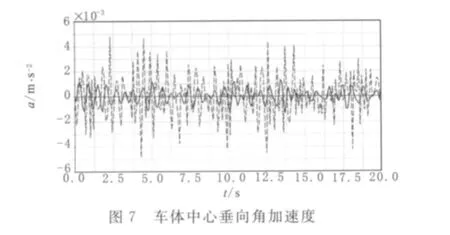
车辆在运行过程中，车体变形较大的部位是二系悬挂连接部位、车窗边部，柔性车体的最大变形量为9.15mm；柔性车体垂向加速度与刚性车体的垂向加速度幅值相差很小，柔性车体的加速度稍大，如图6所示；刚性车体的垂向角加速度比柔性车体的大，如图7所示，但两者也基本属于同一数量级。这表明，将车体考虑为柔性体时，对车体的垂向振动影响并不大，但有所增加。如果将其他零部件也考虑柔性体时，是否对整个轨道车辆的动态性能依然较小，这需要进一步深入研究。

4 结束语

a.在美国5级轨道谱的激励下，某型轨道车辆的线性临界速度为250～300km／h；非线性临界速度为232km／h。

b.该型号的轨道车辆以100km／h的速度通过设置的仿真轨道线路时，安全系数比较高，车辆平稳性指标最大值为2.2，属于优等级；而当该型号的轨道车辆以120km／h的速度行驶时，车辆的平稳性指标为2.85，仅达到合格等级；而当该型号的轨道车辆以140km／h的速度行驶时，车辆的平稳性指标达到了3.2，属于不合格等级。依照平稳性指标的评定等级，该型号的轨道车辆运行速度应低于120km／h。

c.当车速为100km／h，将车体考虑为柔性时，车体的最大变形量为9.15mm；车体的垂向加速度有所增加，但相比刚性车体的加速度幅值差别微小；柔性车体的角加速度与刚性车体相比较却有所下降，但是属于同一数量级别。说明将车体考虑为柔性体时，对车体的垂向振动影响并不大，但有增大的趋势。

[1]傅秀通.专家级动力学分析软件——SIMPACK[J].CAD／CAM 与制造业信息化，2004，（3）：69-70.

[2]缪炳荣，罗 仁，王 哲，等.SIMPACK动力学分析高级教程[M].成都：西南交通大学出版社，2010.

[3]张卫华.轨道车辆车辆动态模拟[M].北京：中国铁道出版社，2006.

[4]缪炳荣，肖守讷，金鼎昌.应用SIMPACK对复杂机车多体系统建模与分析方法的研究[J].机械科学与技术，2006，25（7）：813-817.

[5]Oakar Wallrapp.Flexible muti-body dynamics with space flight applications using SIMPACK[J].Munich University of Applied Sciences，2006，10（1）：286-299.

[6]Shabana.Dynamics of multi-body systems[M].Cambridge University Press，1998.

[7]练松良.轨道动力学[M].上海：同济大学出版社，2003.

[8]Kortum W.Review of muti-body computer codes for vehi-cle system dynamics[J].Vehicle System Dynamics，1993，22（2）：1744-1759.

[9]翟婉明.车辆-轨道耦合动力学[M].北京：中国铁道出版社，1997.

[10]GB50090—2006，铁路线路设计规范[S].

[11]GB5599—85，铁道车辆动力学性能评定和试验鉴定规范[S].

[12]杨继震.宽轨车动力学分析[J].GET Solutions，2011（1）：7-10.