丽江观测站1.8米望远镜自适应光学系统性能初步理论估计*

陈京元，和 成，张定稳，和福瑞，和汉龙，熊耀恒

（中国科学院云南天文台，云南昆明 650011）

丽江观测站1.8米望远镜自适应光学系统性能初步理论估计*

陈京元，和 成，张定稳，和福瑞，和汉龙，熊耀恒

（中国科学院云南天文台，云南昆明 650011）

为了探讨丽江1.8m自适应光学望远镜在天文或天体物理研究领域的可能应用，使用误差基本标度理论对其性能进行了初步的理论分析。结果表明，一般观测条件下，系统分辨力可以达到近似衍射极限。同时对在其上配置激光导星系统后可获得的性能进行了预测，结果表明，激光导星自适应光学系统将大幅度提高系统的天空覆盖率。

大气湍流；天文望远镜；自适应光学；系统分辨力；天空覆盖率

自适应光学（Adaptive Optics，AO）技术［1］通过实时补偿大气湍流效应从而获得系统性能的极大改善，因此广泛用于新的地基天文望远镜系统的设计和制造，而已有的大型地基天文望远镜也已经装备或计划装备相应的自适应光学子系统。带有自适应光学系统的天文望远镜，给当代天文和天体物理的研究带来深远的影响［2］。迄今为止，通过自适应光学系统已获得大批天文和天体物理成果［3］；而且，越来越多的天文和天体物理问题的研究也需要更强大的自适应光学系统的帮助才有可能［4］。

与国外日新月异的进展相比，国内自适应光学技术在天文领域的应用尚处于起步阶段。尽管已经建造并投入使用了数台自适应光学望远镜［5］，但除了为进行系统性能测试而进行的观测外，有科学意义的天文或天体物理成果尚未见报道。为了将已有自适应光学系统应用于具体天文或天体物理问题的观测和研究，还需要相关研究人员的长期努力。

中国科学院成都光电技术研究所最新设计的127单元自适应光学系统是目前国内最先进的自适应光学系统［6］，这一系统已经装备于丽江观测站1.8m望远镜，并已投入使用。为了探讨其在天文或天体物理研究领域可能的应用，本文对其性能进行初步的理论估计。

1 性能理论估计的不同阶次

在自适应光学系统的设计和制造过程的实践中，经验不断地系统化，进而发展成完备的理论体系；另一方面，理论反过来对系统的设计提供基本的指导和依据。在自适应光学系统的分析和设计过程中，普遍使用如下几类复杂程度不同的理论方法：

（1）误差标度律（“零阶”模型）

自适应光学系统的本质在于对光波的大气湍流扰动相位误差进行实时校正，因此相位残余误差总是自适应光学系统关注的核心内容之一。迄今为止，研究者已经识别出自适应光学系统的数十种误差来源，并建立了这些误差方差与其主要控制参数间依赖关系的显式表达式，即通常所谓误差标度律［1，7］。这些关系式大多基于系统的简化假设或某种渐近解，因此，这类方法一般只能提供系统大致的，甚至只是数量级上的估计。但是，由于它们刻画了系统性能与主要控制参数的依赖关系，因此在自适应光学系统的设计中，它们仍然具有基本的重要性。

（2）线性系统模型（“一阶”模型）

一个自适应光学系统的性能由其运行状态决定。从数学的角度，所有运行状态的总和，构成自适应光学系统状态参数空间，而相关的物理过程则表现为此状态空间中算符。自适应光学系统状态空间具有很高的维度（实际上是无穷维Hilbert空间），而物理过程一般则是高度复杂的非线性过程。线性系统模型［8］将有关物理过程简化为线性算符，所以提供了自适应光学系统性能的一种方便的估计工具。相对于误差标度律，线性系统理论考虑了有关误差间的部分统计关联，可以给出优于简单标度律的结果。

另一方面，由于线性系统理论在频谱空间中有更简单的形式（如卷积运算化为乘积运算），因此，自适应光学系统线性理论常常在频谱空间中实现［9-10］。

（3）Monto-Carno数值模拟（“高阶”模型）

研究自适应光学系统的性能，理论上的分析当然是第一选择。然而，这种分析又常常是困难甚至无法实现的：一方面是由于自适应光学系统结构及各子系统相互作用复杂，而且运行在极端复杂的现实环境中；另一方面，自适应光学中所涉及到的众多物理现象（例如大气湍流）仍然是尚未最终攻克的难题。在此背景下，随着计算机应用的普及，以及计算能力的提高，在时间域对自适应光学系统进行Monto-Carno类型的数值模拟［11-12］，在自适应光学的研究中日益受到重视。用计算机对自适应光学系统进行数值模拟具有可行性的依据在于，模拟所需要的物理规律是完全已知的（波动光学），或至少有大致精确的相关结果（如K41湍流理论）。相比前两类方法而言，这类方法原理比较简单，并可以对系统的运行状态进行准确细致的模拟，例如可以研究传输理论中尚未解决的四阶以上的统计量；但另一方面，这种类型的模拟，将对系统软硬件资源提出较高的要求。

本文将以最简单的第一类分析方法为基础，对1.8米望远镜自适应光学系统的性能进行初步的理论分析。

2 主要误差标度律和性能指标

本文只关注来源于大气湍流的高频动态误差，而不考虑系统内部误差，以及由于加工和安装缺陷产生的，或由于温度和重力变形等引起的静态或低频误差。

现代自适应光学系统一般可分解为高精跟踪系统和大气校正系统两个子系统，分别校正大气湍流倾斜和高阶分量。对于大气校正系统，误差方差（即波面误差）的主要来源是：变形镜拟合误差σ2

WF，伺服误差，信标非等晕误差，以及测量误差；而对于高精跟踪系统，误差方差（即倾斜跟踪误差）主要来源于伺服时间误差，信标非等晕误差，以及测量误差。若忽略各误差之间的统计关联，则可以将自适应光学系统主要误差方差写为：

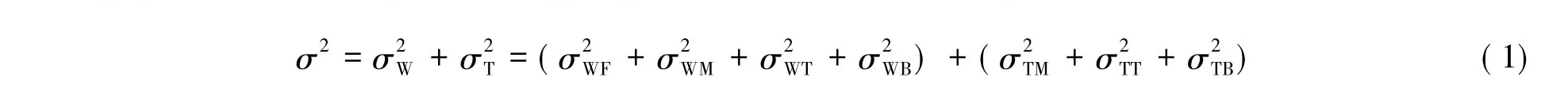
下面几节中，列出本文所用的各有关标度律。

2.1 变形镜拟合误差

变形镜拟合误差可以标度为［13］：

式中，d为自适应光学系统驱动器间距；AF为变形镜拟合常数，它与变形镜种类及具体配置情况有关，一般可取AF≈0.3；特征量r0为大气相干尺度，定义为：

这里ξ和μm分别表示目标天顶角和湍流结构函数m阶矩。

2.2 控制系统伺服误差

若将系统等效为总延迟时间τsw的纯延迟系统，则伺服误差标度为［14］：

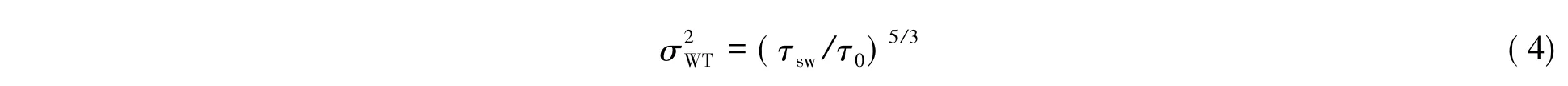
式中，特征量τ0为大气湍流相干时间，定义为：

式中，νm表示湍流m阶速度矩。总延迟时间一般定义为：

式中，τiw和ξw分别表示波前传感器积分时间和变形镜校正延迟时间。

类似地，高精跟踪系统伺服误差标度为［7］：

这里的特征量τ1定义为：

而高精校正系统总延迟时间为：

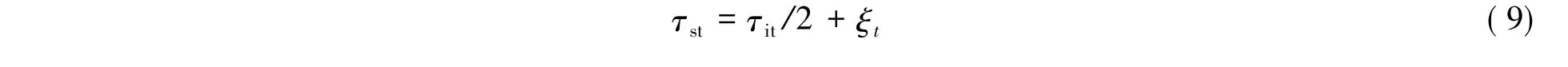
式中，τit和ξt分别表示高精传感器积分时间和倾斜镜校正延迟时间。也常将控制系统等效为Type-1型侍服系统，此时伺服误差标度为：

式中，f3db和ft3db分别表示大气和高精系统3 db有效控制带宽；对一般带宽优化的自适应光学系统，其大小约为波前探测器采样频率的十分之一。这里有关的特征量为Greenwood频率和Tyler频率，定义分别为：

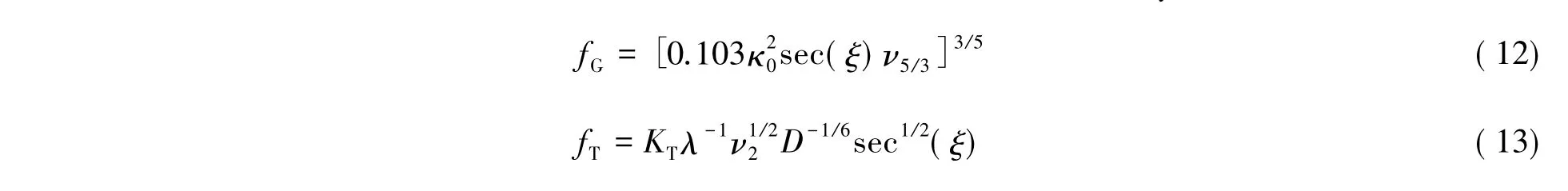
这里常数KT对于Z倾斜和G倾斜各不相同，分别约为0.368和0.331。

本文后面的计算中，将自适应光学系统等效为纯延迟系统。

2.3 信标非等晕误差

根据信标的具体使用情况，自适应光学系统非等晕误差有不同的表现形式。如果使用自然信标NGS检测大气湍流，则此时非等晕误差主要是角度非等晕，记信标和目标偏角θ，则此误差项可标度为［15］：

其中的特征量大气等晕角定义为：

NGS角度非等晕性对系统的性能有很大的制约，为克服NGS角度非等晕的限制，现代自适应光学系统一般使用LGS和NGS分别检测大气湍流高阶和低阶模式（例如倾斜分量）。这时非等晕误差主要是NGS的角度倾斜非等晕以及LGS的聚焦非等晕误差，NGS的角度倾斜非等晕误差可以标度为［7］：

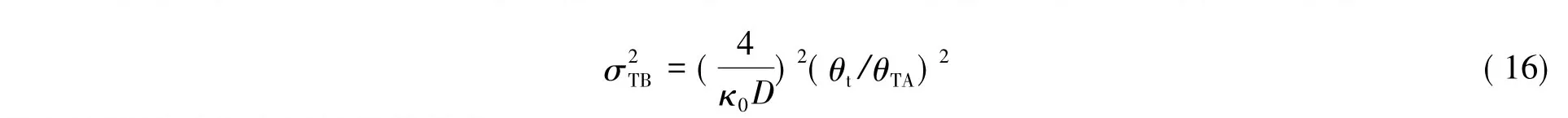
其中的特征量为大气倾斜等晕角：

而LGS的聚焦非等晕误差则标度为［16］：其中特征量为LGS有效口径，其大小近似为：

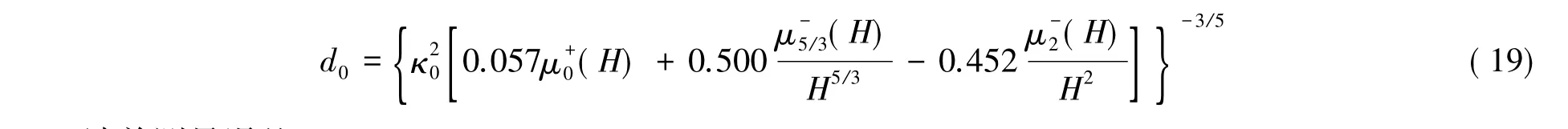
2.4 波前测量误差

对大气校正和高精跟踪系统，测量误差分别标度为［1］：

式中，εp为波前重构中噪声传播因子；χt和χw为闭环平均因子；σst和σsw分别表示传感器子孔径所测光斑大小；SNR表示探测器信噪比。

噪声重构传播因子εp与波前重构算法有关，其具体求解表达式为εp=Trace［（ATA）-1］/Na，这里A表示重构矩阵；Na表示重构自由度即变形镜驱动器个数；Trace表示矩阵求迹运算。当Na较大时，可使用近似关系εp≈0.1+0.16ln（Na）。

两个闭环平均因子的求解表达式［17］可统一写为（2/κ）tan-1（κ/2），其中κ为采样频率与控制带宽之比，即对高精系统，κ≡fst/ft3db，而对大气校正系统κ≡fs/f3db。

对Shack-Hartman型的波前传感器，子孔光斑大小为：

式中，Kq表示探测单元间空隙的影响因子；λB和θB分别表示信标波长和角尺寸大小，如用钠信标，则λB=589 nm；λS表示探测器中心波长；rm表示有效的成像孔径尺寸，应由子孔大小d和大气相干长度r0中的小者决定，即rm=min{d，r0}。

对于大气整体倾斜探测器，所测光斑大小可表示为：

式中，rm=min{D，r0}

探测器信噪比SNR可以表示为：

这里已计入背景噪声及读出噪声的贡献。式中，nP为有效光子数；nb表示背景噪声，对于夜晚可见光波段探测器，该项可以忽略；一般使用的平方探测器，即ND=4；Ge为强度增益系数。

探测有效光子数与所用信标光源的类型有关。对一般脉冲型LGS信标光源，有效光子数可以表示为nP=ηMPTWNP，其中η为光子探测量子效率；MP为探测器积分时间内所接收光脉冲数目；TW表示从波前传感器到平方探测器的光透射率；NP是每个子孔径从每脉冲光中所获得的光子数，其大小由激光雷达方程确定：

式中，FB称为信标效率因子，表示单位脉冲能量单位面积所接收光子数目，这一因子将后向散射截面σB、散射体数密度n（H）、散射层厚度ΔR、信标高度H以及大气透过率TA等因素并合在一起；E为激光器单位脉冲能量；TL与To分别表示从激光器光出口到激光发射主镜，以及从发射主镜到波前传感器路径上的光透射率。

NGS为宽谱连续型光源，有效光子数可以表示为nP=ητsTWNS，这里τs为探测器有效积分时间； NS为光子流（单位时间流入光子数）大小，对于中心探测波长λS约为550 nm的探测器，光子流可以用NGS视星等mv表示为：这里Δλ为探测带宽。

2.5 自适应光学系统校正性能评估指标

一般用Strehl比及系统成像角分辩率（常用FWHM量度）作为自适应光学系统性能的评价指标。另外，天文自适应光学系统性能的评估，一个非常重要的指标是天空覆盖率。本文将以这3个指标作为性能评估的基准。

当通过大气湍流成像时，短曝光像由衍射极限主瓣和覆盖直径λ/r0为区域的一组旁瓣组成，主旁瓣间能量的比值取决于去除倾斜后的波面误差的大小。对于长曝光成像，随机波动的旁瓣平均后构成光滑的背景环，并由于未校正的光束抖动而使整个图形加宽。所以一般长曝光像的点扩展函数可以描述为由倾斜跟踪误差σ2T所确定的主瓣，以及由去除倾斜后的波面误差σ2W所决定的旁瓣的组合。于是湍流像的峰值能量即Strehl比可近似写为主旁瓣能量峰值之叠加即：

而对长曝光像，由于跟踪抖动误差的影响，主旁瓣能量峰值将有一定程度的衰减，其大小可分别表示为：于是长曝光Strehl比近似为：

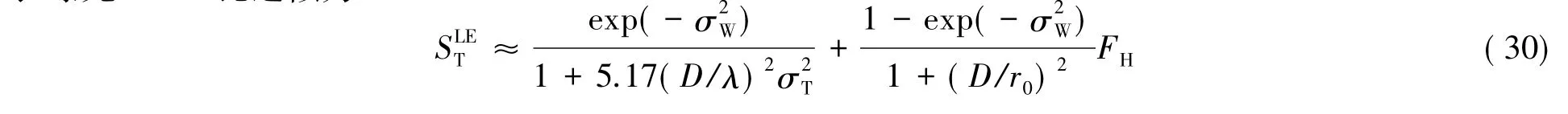
系统成像角分辩率（FWHM）可以用Strehl比近似为：

天空覆盖率是天文自适应光学望远镜性能的一个综合指标。使用很靠近观测目标的较亮的自然信标，固然可获得较好的校正性能，但这样的自然信标很难找到；另一方面，减小自然信标亮度或增加其与目标间距离，尽管由于探测信噪比减小或角度不等晕误差增加从而导致系统性能降低，但可以提高找到合适自然信标的概率。一般将系统性能达到一定标准（如获得Strehl比S0）时的概率定义为天空覆盖率。若假设视星等为mv的恒星按照随银纬b缓慢变化的密度函数ρ（mv，b）以Poisson分布方式随机布满整个天空，则天空覆盖率可以写为：

这里θ（S0，Mv）表示NGS视星等为mv时，若系统Strehl比达到S0时所允许的最大目标与NGS偏角。其中求最大算符遍及所有恒星视星等。

3 计算模型和基本参数

模型参数主要包括系统参数和环境参数。系统参数主要是望远镜系统参数，自适应光学系统参数，以及激光信标系统参数；环境参数包括大气湍流和横向风速度参数，激光信标大气后向散射截面参数，以及计算天空覆盖率所需的银河系恒星密度模型等。下面列出本文采用的主要模型和计算参数。

3.1 系统主要参数

这里列出本文1.8m望远镜自适应光学系统的一些主要系统参数大小［6］。对于文献中未明确指出的一些必需参数以及激光信标系统参数（目前1.8m望远镜激光信标校正模式尚未实现），选择当前一般技术发展水平的参数大小。

系统有效口径：D=1.8m；

大气变形镜单元数：Na=127；

探测器子孔径大小d=D/13≈0.14m；

波前探测器中心波长550 nm，Δλ=300 nm为波前探测波段；

信标光中心波长：对NGS取550 nm；对LGS取589 nm；

波前探测频率fs：500Hz，1 000 Hz，及2 000 Hz可调，本文计算1 000 Hz情形；

高精跟踪探测频率fst：100～500Hz可调。本文计算200 Hz情形；

对应的积分时间分别为τiw=1ms，τit=5ms；

校正时间延迟：ξw，ξt，假设为1ms；

激光信标系统：假设LGS发射功率10w，重复频率1 000 Hz；

其它有关参数：Kq=1.4；e=4；nb=0；ND=4；Ge=1；η=0.8；TW=0.8；TL=0.5；To=0.5；TA=0.7

3.2 大气模型和参数

考虑到丽江观测站的典型大气状况［18-19］，采用有关经典模型描述地球大气。湍谱以K41模型模拟，湍流结构常数采用Hufnagal-Valley剖面模型：

另外，以经典的Bufton风模型：

模拟大气横向风速度的大小。下面计算中假设Vt=3Vg。

关于大气后向散射截面的模型和数据参见文献［1］的列表。

3.3 恒星密度模型

采用Bachall＆Soneira恒星密度模型［20］。银经l，银纬b处，单位平方弧度面积内亮度大于mv的恒星数目可以用下面表达式求出：

式中，σ=1.45-0.2cos b cos l；C1=925；α=-0.132；β=0.035；δ=3.0；m*=15.75；C2=1 050；κ=-0.180；η=0.087；λ=2.50；m+=17.5

下面计算中，设l=0°，b=20°。其它位置处结果稍有不同。

4 一些计算结果

根据前述标度率和有关模型参数，即可对系统的基本性能进行定量的估计。这一部分将以图表的方式给出一些计算结果，包括不同信标模式（自然信标、瑞利信标、钠信标等）下系统的基本性能；不同校正波长下（中心波长分别为0.85μm、1.26μm、1.62μm、2.21μm的I、J、H、K波段）系统主要性能；一般条件和场景下系统主要残余误差和性能指标的典型大小；系统性能随外界环境（大气湍流、风速度等）的变动关系；信标无偏置（On-axis）时的校正性能；信标有偏置时的校正效果及天空覆盖率的大小等等。通过这些结果，可获得1.8m望远镜自适应光学系统性能比较全面的认识。

4.1 信标无偏置时的校正性能

当观测目标足够亮时，可直接用其作为自然信标，这时没有角度不等晕误差。首先给出这种情况下主要误差以及性能指标的典型大小。综合有关文献［18-19］的结果，丽江观测站大气相干尺度平均值约为10 cm（对500 nm参考波长），地面平均风速度约为5m/s。以此平均值为基准，可以估计出系统各主要误差和性能指标的大小，结果如表1。需要注意，计算中假设倾斜分量由单独的自然信标子系统校正；自然信标的视星等取8；瑞利信标和钠信标海拔高度分别取20 km和90 km。

表1 系统主要误差以及性能指标的典型大小Table 1 Typical values ofmain errors and key parameters of the system

可以看到在此条件下，采用钠信标与自然信标校正时误差和校正性能大体相当，RMS约为70 nm；而采用瑞利信标，系统残余误差有些增加，RMS约为120 nm。注意到对I、J、H、K波段，衍射极限分辨力分别为118.831mas、176.150mas、226.479mas和308.962mas，由图中数据可见系统分辨力已接近衍射极限。只有当使用瑞利信标模式校正I波段时系统FWHM较大，约为1.4倍衍射极限。

气象条件并非固定不变的，而是随着时间变化发展的；在丽江观测站，大气相干尺度可在5 cm到25 cm之间变动，而地面极端风速度可达20m/s。图1～2反应了自适应光学系统校正性能随气象条件的变化关系。

系统校正性能随湍流强度的变化关系见图1。其中图1（a）与图1（b）示出在4种校正波长和自然信标校正模式下，性能随湍流强度的变化；图1（c）与1（d）示出分别使用自然信标、10 km和20 km瑞利信标以及90 km钠信标4种不同信标模式校正I波段时，性能随湍流强度的变化。图中数据对应地面风速度为5m/s。

图1 自适应光学系统性能随湍流强度的变化关系：（a）不同校正波长下Strehl比；（b）不同校正波长下分辨力；（c）不同信标模式下Strehl比；（d）不同信标模式下分辨力Fig.1 Dependence of the performance of an AO system on turbulence intensity.（a）Strehl ratios for different wavelengths；（b）resolutions for differentwavelengths；（c）Strehl ratios for different beacons；（d）resolutions for different beacons

系统校正性能随地面风速度的变化关系见图2。其中图2（a）与图2（b）示出在4种校正波长和自然信标校正模式下性能随风速度大小的变化；图2（c）与图2（d）示出分别使用自然信标、10 km和20 km瑞利信标已经90 km钠信标校正I波段波长时，性能随风速度大小的变化。图中数据对应大气相干长度10 cm（对500 nm参考波长）。

综合有关数据可以将当观测目标足够亮时，系统性能随气象条件变化的大致范围总结如下表2。可以看到，即使在极端恶劣气象条件下，使用瑞利信标模式校正I波段光波，系统分辨力也可达到约2.1倍衍射极限。

表2 系统性能随着大气条件的变化范围Tab le 2 Variation ranges of system parameters due to atmospheric changes

图2 自适应光学系统校正性能随地面风速度的变化关系：（a）不同校正波长下Strehl比；（b）不同校正波长下分辨力；（c）不同信标模式下Strehl比；（d）不同信标模式下分辨力Fig.2 Dependence of the performance of an AO system on ground-level wind velocity.（a）Strehl ratios for differentwavelengths；（b）resolutions for differentwavelengths；（c）Strehl ratios for different beacons；（d）resolutions for different beacons

系统校正性能随自然信标视星等的变化关系见图3。图中对应大气相干尺度10 cm（500 nm参考波长），地面风速度5m/s时情形。其中图3（a）与图3（b）示出在4种校正波长和自然信标校正模式下，性能随自然信标视星等的变化。可以看到，当mv＜8时（即自然信标较亮时），系统性能变化不大；而当mv＞10时，测量误差处于支配地位，系统性能急剧下降。

图3（c）与图3（d）示出使用自然信标、10 km和20 km瑞利信标以及90 km钠信标校正I波段光波时，系统性能随自然信标视星等的变化。可以看到，对于激光信标校正模式，当mv＞15时，系统性能方才显著恶化。因此，使用激光信标，大大扩展了可观测范围。

4.2 角度非等晕与天空覆盖率

如果使用与目标不在同一方向的自然信标，则由于角度不等晕的影响，系统性能将会下降；然而另一方面，这样可以提高天空覆盖率。图4示出了I波段和K波段天空覆盖率和系统性能的这种竞争关系。图中实虚线分别对应钠信标校正模式下Strehl比及天空覆盖率的等值线，而横纵坐标分别表示自然信标视星等和信标目标间偏角大小。

进一步，根据（32）式可以求出天空覆盖率和自适应光学系统Strehl比之间的变化关系。图5示出I波段和K波段下不同自适应光学校正模式时天空覆盖率和Strehl比之间的变化关系。可以看到，在I波段，当使用自然信标校正时，与Strehl比分别为5％、10％和30％对应的天空覆盖率分别为1.5× 10-4、8.5×10-5和2.3×10-5；而使用激光信标，对应的天空覆盖率则约为40％、10％和0.5％。在K波段，当使用自然信标校正时，与Strehl比分别为10％、30％和50％对应的天空覆盖率分别为40％、0.11％和3×10-4；而使用激光信标，对应的天空覆盖率则分别约为99％、40％和5％。可见使用人工激光信标大幅度提高了自适应光学系统天空覆盖率。

图3 自适应光学系统校正性随自然信标视星等的变化关系：（a）不同校正波长下Strehl比；（b）不同校正波长下分辨力；（c）不同信标模式下Strehl比；（d）不同信标模式下分辨力Fig.3 Dependence of the performance of an AO systems on apparentmagnitudes of NGS.（a）Strehl ratios for differentwavelengths；（b）resolutions for differentwavelengths；（c）Strehl ratios for different beacons；（d）resolutions for different beacons

图4 Strehl比与天空覆盖率间变化关系：（a）I波段；（b）K波段Fig.4 Strehl ratio vs.sky coverage：（a）for the Iband，and（b）for the K band

图5 不同信标模式下天空覆盖率：（a）I波段；（b）K波段Fig.5 Sky coverages of different beacons：（a）for the Iband，and（b）for the K band

图6示出自然信标和钠信标校正模式下与不同校正波长对应的天空覆盖率和Strehl比之间的变化关系。使用钠信标，可以分别将I、J、H、K波段对应Strehl比30％的天空覆盖率从5.28×10-6、5.51× 10-5、1.44×10-4和5.69×10-4提高到0.63％、3.6％、12％、47％。

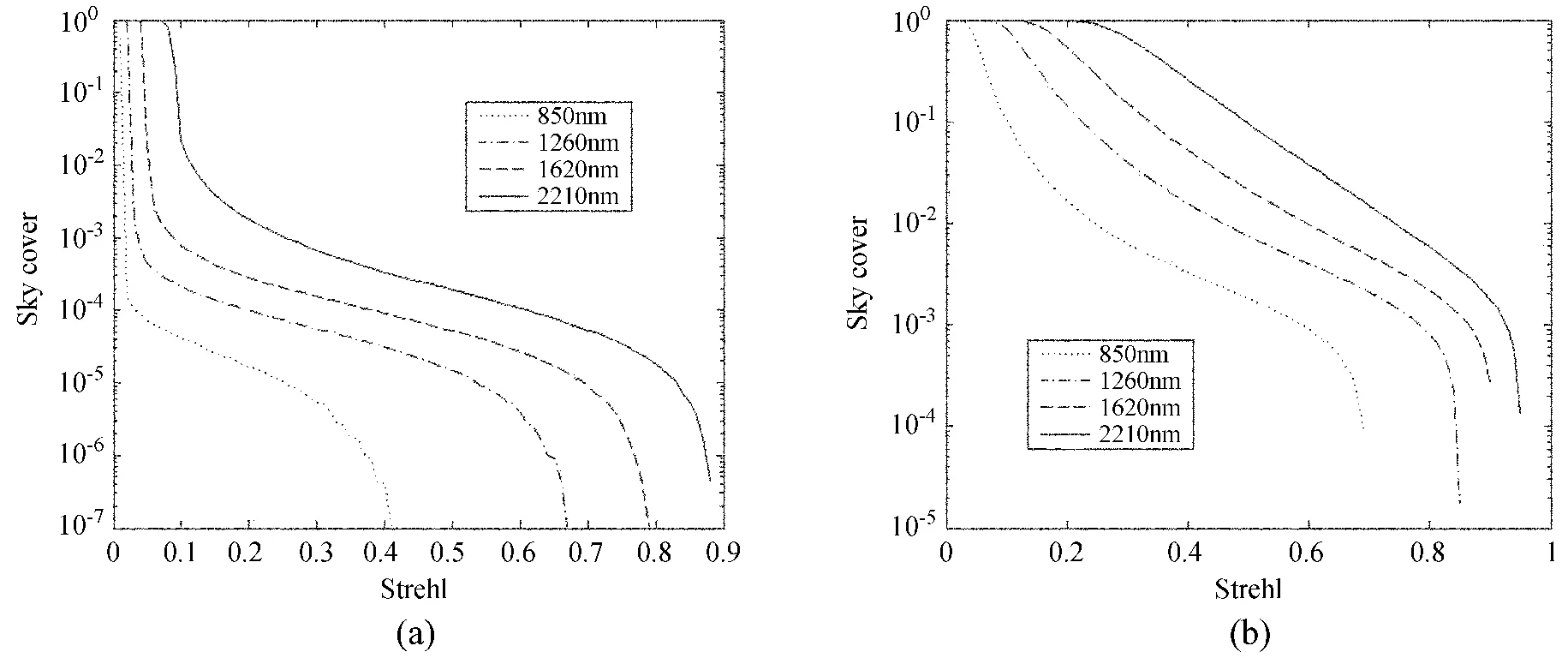
图6 不同波段和信标模式下天空覆盖率：（a）NGS；（b）LGSFig.6 Sky coverages for differentwavelengths of the beacons（a）for the NGS，and（b）for the LGS

5 小结

以误差标度律为基础，结合丽江观测站一般大气条件，对1.8m望远镜自适应光学系统主要残余误差和基本性能进行了初步的分析和估计。结果表明，一般气象条件下观测较亮天体，系统可达到近似衍射极限的分辨力；观测较暗天体时，由于信噪比的降低，测量误差居于主导地位，系统性能大幅度下降。同是以当前一般技术水平为基础，对1.8m望远镜激光导星自适应光学系统的性能进行了预测。结果表明，一般气象条件下观测较亮天体，系统仍有接近衍射极限的分辨力；即使在极端恶劣的气象条件下使用瑞利信标模式校正I波段，系统仍有约2倍衍射极限分辨力。计算结果也表明，使用激光信标模式，将会大大提高自适应光学系统天空覆盖率。

如前文指出，本文使用的误差标度律只提供了系统性能最粗略的一种估计。为了获得系统更准确细致的性能评估，需要使用更高阶的理论模型或数值模拟。将在后续文章中使用高阶模型对1.8m望远镜自适应光学系统性能给出进一步的分析，以便给其在天文或天体物理领域的应用研究提供技术上的指导和依据。

［1］Hardy JW.Adaptive optics for astronomical telescopes［M］.Oxford：Oxford University Press，1998.

［2］Pierre Léna.Adaptive optics：a breakthrough in astronomy［J］.Experimental Astronomy，2009，26（1）：35-48.

［3］Laird M Close.A review of published adaptive optics science：a bright future for adaptive optics［J］.Proceedings of SPIE，2003，4834：84-100.

［4］Gilmozzi R.Science and technology drivers for future giant telescopes［J］.Proceedings of SPIE，2004，5489：1-10.

［5］姜文汉，张雨东，饶长辉，等.中国科学院光电技术研究所的自适应光学研究进展［J］.光学学报，2011，31（9）：1-9.Jiang Wenhan，Zhang Yudong，Rao Changhui，et al.Progress on adaptive optics of institute of optics and electronics，Chinese Academy of Science［J］.Acta Optica Sinica，2011，31（9）：1-9.

［6］Rao C H，JiangW H，Zhang Y D，etal.Progress on the 127-elementadaptive optical system for 1.8m telescope［J］.Proceedings of SPIE，2008，7015：70155Y.

［7］Tyler G A.Bandwith considerations for tracking through turbulence［J］.Journal of the Optical Society of America A，1994，11（1）：358-367.

［8］Ellerbroek B L.First-order performance evaluation of adaptive-optics systems for atmosphericturbulence compensation in extended field of view astronomical telescopes［J］.Journal of the Optical Society of America A，1994，11（2）：783-805.

［9］Jolissaint J，Veran J P.Analyticalmodeling of adaptive optics-foundations of the phase spatial power spectrum approach［J］.Journal of the Optical Society of America A，2006，23（2）：382 -394.

［10］ 陈京元，李有宽.激光导星自适应光学系统一阶理论模型［J］.强激光与粒子束，2009，21（5）：649-657.Chen Jingyuan，Li Youkuan.First-order theoretical model for laser guider star adaptive optics system［J］.High Power Laser and Particle Beams，2009，21（5）：649-657.

［11］ CarbilletM，Verinaud C，Femenia B，et al.Modeling astronomical adaptive optics［J］.Monthly Notices of the Royal Astronomical Society，2005，365（4）：1263-1275.

［12］ 陈京元，甘光勇，陶应学.SciAO：自适应光学建模与仿真 ［J］.系统仿真学报，2008，20（11）：2864-2867.Chen Jingyuan，Gan Guangyong，Tao Yingxue.SciAO：Modeling and simulation of adaptive optics［J］.Journal of system simulation，2008，20（11）：2864-2867.

［13］Greenwood D P.Mutual coherence function of a wave front corrected by zonal adaptive optics［J］.Journal of the Optical Society of America，1979，69（4）：549-554.

［14］Fried D L.Time-delay-induced mean-square error in adaptive optics［J］.Journal of the Optical Society of America A，1990，7（7）：1224-1225.

［15］Fried D L.Anisoplanatism in adaptive optics［J］.Journal of the Optical Society of America，1982，72（1）：52-61.

［16］Tyler G A.Rapid evaluation of d0：the effective diameter of a laser-guide-star adaptive-optics system［J］.Journal of the Optical Society of America A，1994，11（1）：325-338.

［17］ Gavel D T，Morris JR，Vernon R G.Systematic design and analysis of laser-guide-star adaptiveoptics systems for large telescopes［J］.Journal of the Optical Society of America A，1994，11（2）：914-924.

［18］ 云南天文台选址组.丽江高美古的气象条件［J］.天文学报，1999，40（3）：326-334.Site Testing Group of Yunnan Astronomical Observatory.The astro-climatic conditions at GaoMeiGu of LiJiang county［J］.Acta Astronomica Sinica，1999，40（3）：326-334.

［19］ 云南天文台选址组.丽江高美古的天文观测条件［J］.天文学报，1999，40（3）：319-325.Site Testing Group of Yunnan Astronomical Observatory.Site testing at Gaomeigu in Lijiang county-seeing，sky brightness and extinction coefficient［J］.Acta Astronomica Sinica，1999，40（3）：319-325.

［20］ Bahcall JN，Soneira R M.The universe at faintmagnitudes.I-Models for the galaxy and the predicted star counts［J］.Astrophysical Journal Supplement Series，1980，44：73-110.

A Performance Evaluation of the Adaptive-optics System for the 1.8m Astronom ical Telescope at the Lijiang Observational Station

Chen Jingyuan，He Cheng，Zhang Dingwen，He Furui，He Hanlong，Xiong Yaoheng
（Yunnan Observatories，Chinese Academy of Sciences，Kunming 650011，China，Email：chenjingyuan@ynao.ac.cn）

In order to investigate potential applications of the 1.8m telescope equipped with an autoguiding stellar adaptive-optics system at the Lijiang observational station，we give a preliminary performance evaluation of this adaptive-optics system by using the theory of scaling of residual phase variances proposed by us.The results show that under usual observational conditions the angular resolution of the system is almost diffraction-limited.We also give an analysis of the performance when a laser guide subsystem is equipped on this adaptive-optics system，and our calculations show that the sky coverage will be consequently greatly improved.

Atmospheric turbulence；Astronomical telescope；Adaptive optics；Resolution；Sky coverage

O43

：A

：1672-7673（2013）03-0308-13

国家自然科学基金（10978025）资助.

2012-06-06；修定日期：2012-08-01

陈京元，男，副研究员.研究方向：自适应光学的天文应用.Email：chenjingyuan@ynao.ac.cn

CN 53-1189/P ISSN 1672-7673